Методические указания к решению задач К3.1, К3.2

Содержание контрольной работы

КОНТРОЛЬНАЯ РАБОТА № 3

Контрольные работы, выбор данных для них

Проведение расчетов

Для снижения трудоемкости решения и числа вычислительных ошибок рекомендуется выполнять расчеты в алгебраическом виде до конечного результата. Для получения численного решения необхо­димо в формулу подставлять числовые значения входящих в нее кон­стант и переменных в основных единицах СИ и в том порядке, в ко­тором они расположены в алгебраическом выражении. После прове­дения необходимых математических действий результат решения должен быть записан также в основных единицах СИ. Далее он для удобства восприятия может быть выражен в кратных единицах. Ука­зание единиц измерения результата обязательно.

В расчетах на прочность, жесткость и устойчивость, как пра­вило, допускается отклонение от нормативных данных (допускаемое напряжение, допускаемые деформации, коэффициент запаса) в пре­делах ± 5 %. В связи с этим достаточным является представление чи­сел с точностью до третьей значащей цифры. Рекомендуется там, где это удобно, записывать числа с указанием десятичного порядка, на­пример: 160 000 000 – 160×10⁶; 0,0008356 – 8,36×10^-4 и т.д.

При изучении второй части курса студенты выполняют две контроль­ные работы.

Контрольная работа № 3 содержит задачи К3.1…К3.4. Кон­трольная ра­бота № 4 – задачи К4.1…К4.4.

К каждой задаче дается десять вариантов расчетных схем и таблица с данными к ним.

Студенты выбирают для решения всех задач вариант расчет­ных схем, номер которого совпадает с последней цифрой индивиду­ального шифра. Данные к задачам берутся из соответствующих таб­лиц в столбце или строке, номер которых совпадает с предпоследней цифрой этого шифра. Допустим, шифр оканчивается числом 46. Расчетные схемы за­дач выбираются по варианту № 6, данные – из столбца или строки с номе­ром 4 для всех контрольных работ.

Примечание. Преподаватель может задавать расчётные схемы и исходные данные в ином порядке, но в объеме заданий, приведённых в данном пособии.

Задача К 3.1

Для балки постоянного поперечного сечения (рис. 1) подоб­рать двутавровое сечение из условия прочности по нормальным на­пряжениям и заданного условия жесткости в точке D или точке С. Проверить прочность двутавра по касательным напряжениям. Исходные дан­ные: [s] = 160 МПа, [ t ] = 100 МПа, Е = 2×10⁵ МПа, [ q_с ] = = 1×10^-3 рад, 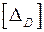= 2×10^{-3 м, а = 2 м. Остальные данные взять из табл. 1.}

Таблица 1

№ строки	Р (qа)	М (qа^2)	q (кН/м)	к
				0,5 0,5 0,5

Задача К 3.2

Для рамы (рис. 2) из условия прочности по нормальным напряже­ниям найти допускаемое значение интенсивности равномерно рас­пределенной нагрузки [ q ].

Исходные данные: [s] = 180 МПа, l = 1,5 м. Остальные данные взять из табл. 2.

Рис. 1

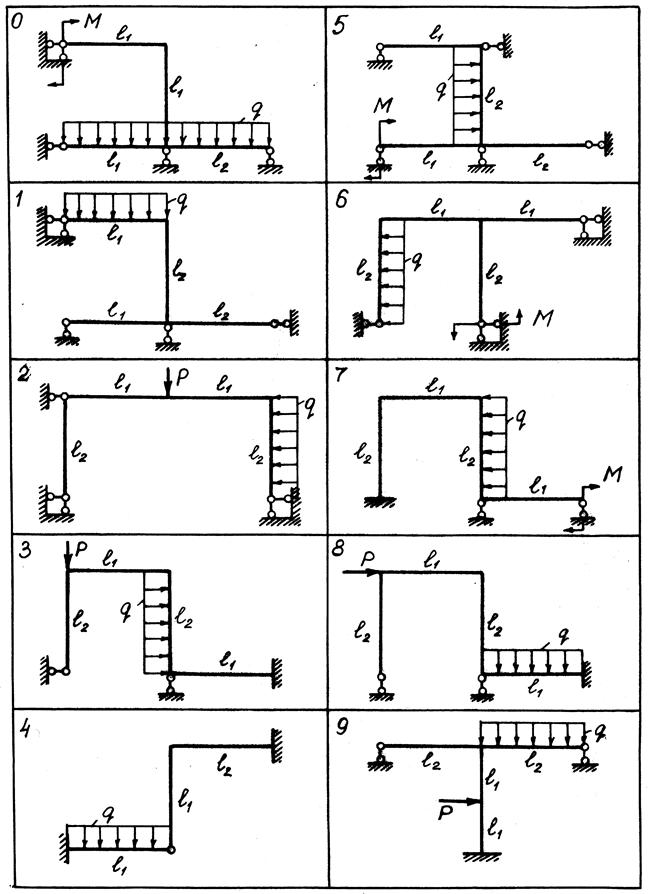Рис.2

Таблица 2

№ строки	l1	l2	Р (ql)	М (ql^2)	Сечение, швеллер
	2 l	l	1,5	1,0	№ 14
	l l	2 l 3 l		1,5	№ 16 № 18
	2 l 3 l	3 l l	0,5	2,5	№ 20 № 24
	0,5 l 2 l	2 l 0,5 l		2,5 2,0	№ 24 № 22
	3 l l	0,5 l 1,5 l		1,5 1,0	№ 18 № 20
	1,5 l	2 l		1,0	№ 16

Задача К 3.3

Для заданного плоского напряженного состояния (рис. 3) тре­буется найти:

а) главные напряжения и их направления, показать главные напряжения на схеме напряженного состояния;

б) максимальные касательные напряжения;

в) эквивалентные напряжения по третьей и четвертой теории прочности;

г) главные деформации ε_1, ε₂ и ε₃ .

Принять Е = 2×10⁵ МПа, m= 0,3. Остальные исходные данные взять из табл. 3.

	Рис. 3

Рис. 3

Таблица 3

№ строки	Задача К 3.3	Задача К 3.4
σx	σy	tху	а	D 1	D2	b	c	N квт	ω рад/cек
МПа	мм
							1,5 а а 1,5 а 2 а 1,5 а 2 а а 1,5 а 2 а 2,5 а	2 а 2 а 3 а 1,5 а а а 3 а 1,5 а 2 а 1,5 а

Задача К 3.4

Для круглого вала постоянного поперечного сечения, вращающегося с угловой скоростью w и передающего мощность N со шкива D ₁ на шкив D ₂, требуется определить:

а) необходимый диаметр вала по третьей и четвертой теории прочности;

б) перемещение оси вала в месте расположения шкива D ₂ и направление этого перемещения.

Принять [s] = 80 МПа, Е = 2×10⁵ МПа, остальные исходные данные взять из табл. 3. Варианты расчетных схем представлены на рис. 4.

	Рис. 4

Рис. 4

Расчетные схемы задач К3.1 и К3.2 являются статически неопре­делимыми.

Система (расчетная схема) называется статически неопредели­мой, если общее число связей, наложенных на систему, больше числа связей, необходи­мых для обеспечения ее равновесия и геометриче­ской неизменяемости. Связи, наложенные на систему сверх необхо­димых, называются дополнительными или «лишними». Естественно, что «лишние» они только с точки зрения равновесия системы. Нали­чие таких связей чаще всего приво­дит к снижению значения внутренних сило­вых факторов в элементах системы, что способствует повышению ее несущей способности и экономичности.

Для расчета стержневой системы на прочность или жесткость необхо­димо определить реакции в связях, наложенных на эту сис­тему. В статически неопределимых системах реакции в дополнитель­ных и необходимых связях определяют раздельно и разными мето­дами. Сначала, используя специальные методы, определяют реакции в дополнительных связях, а затем обычным способом (из уравнений равновесия) определяют реакции в необходимых связях.

В сопротивлении материалов для определения реакций в допол­нительных связях применяется метод сил. В основе этого метода ле­жит простое и ясное физическое представление. Поскольку переме­щения точек приложения связей по направлению этих связей всегда известны (при беззазорном соединении они равны нулю, при наличии зазора – величине зазора), то, составляя выражения для определения этих перемещений, получают уравнения для определения реакций в дополнительных связях. Такие уравнения называются каноническими уравнениями метода сил. С точки зрения математики это система ли­нейных алгебраических уравнений.

Дата добавления: 2015-06-30