Определение перемещений методом Мора

Метод Мора позволяет определять линейные и угловые переме­щения любых сечений любой расчетной схемы по любому направ­лению от действия любых нагрузок.

Коротко напомним порядок определения перемещений методом Мора.

Для определения перемещений методом Мора необходимо:

1. Изобразить расчетную схему конструкции – грузовое состояние.

2. Изобразить вспомогательное состояние – расчетную схему, ос­вобожденную от всех нагрузок. Приложить к вспомогательному со­стоянию в точке, где определяется перемещение, по направлению этого перемещения единичный силовой фактор – силу, равную без­размерной единице, если определяется линейное перемещение, или момент, равный безразмерной единице, если определяется угловое пе­ремещение.

3. Грузовое и вспомогательное состояние разделить на одинаковое число участков. Границами участков являются сечения, где приложены сосредоточенные силы или моменты, в том числе и единичные, начина­ются или кончаются распределенные нагрузки, узлы рамы, а также точки на расчетной схеме, в которых изменяется поперечное сечение. Пронумеровать участки. Порядок нумерации и порядок обхода участков для грузового и вспо­могательного состояния должны быть одинаковыми. Для произволь­ного сечения каждого участка записать аналитические выражения для определения внутренних силовых факторов, возникающих в гру­зовом и вспомогательном состояниях.

4. Полученные аналитические выражения подставить в фор­мулу Мора и произвести необходимые вычисления, в результате этих вы­числений получают искомое перемещение. Если искомое переме­ще­ние получено со знаком «плюс», то это означает, что его направ­ление совпадает с направлением единичного силового фактора. Знак «ми­нус» при перемещении означает, что действительное направле­ние пе­ремещения противоположно направлению единичного сило­вого фак­тора.

Общий вид формулы Мора

.

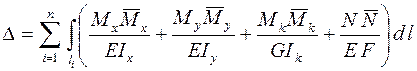(3.1)

Для плоской системы формула (3.1) принимает вид

.

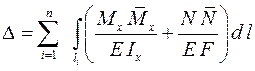(3.2)

Примечание. В формулах (3.1) и (3.2) опущены слагаемые, учитывающие влияние Q_x и Q_y на величину искомого перемещения, так как в технических расчетах этим влиянием пренебре­гают ввиду его малости.

В балках и плоских рамах в большинстве случаев пренебрегают и влиянием N, тогда перемещения определяют по формуле

.

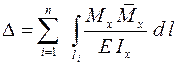(3.3)

В шарнирных фермах, состоящих из прямых стержней, в фор­муле Мора сохраняется лишь член, учитывающий только нормаль­ную силу

.

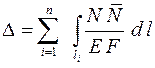(3.4)

В формулах (3.1)…(3.4):

n – число участков интегрирования;

i – номер участка;

l_i – длина участка;

M_x, M_y, M_k, N – аналитические выражения для определения внутренних силовых факторов в грузовом состоянии;

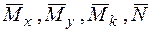– то же во вспомогательном состоянии;

E, G – модуль упругости и модуль сдвига соответст­венно;

I_x, I_y, I_k, F – геометрические характеристики поперечного сече­ния.

Для прямолинейных участков с постоянной жесткостью инте­гралы Мора можно вычислять графоаналитическим способом – спо­собом Верещагина. Способ Верещагина иногда называют способом «перемножения» эпюр. Чтобы им воспользоваться, необхо­димо построить эпюры для грузового и вспомогательного состояний.

Формулы (3.1)…(3.4) в этом случае принимают вид

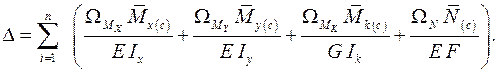
	(3.1а)
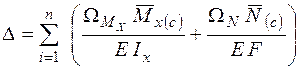.	(3.2а)

.

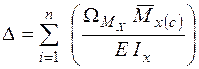(3.3а)

.

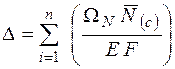(3.4а)

В формулах (3.1а)…(3.4а):

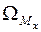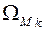, , , W _N – площади грузовых эпюр на i -м участке;

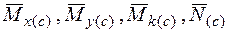– ординаты единичных эпюр (эпюр для вспомогательного состояния) i -го участка, взятые в тех сечениях, где расположены центры тяжести площадей грузовых эпюр.

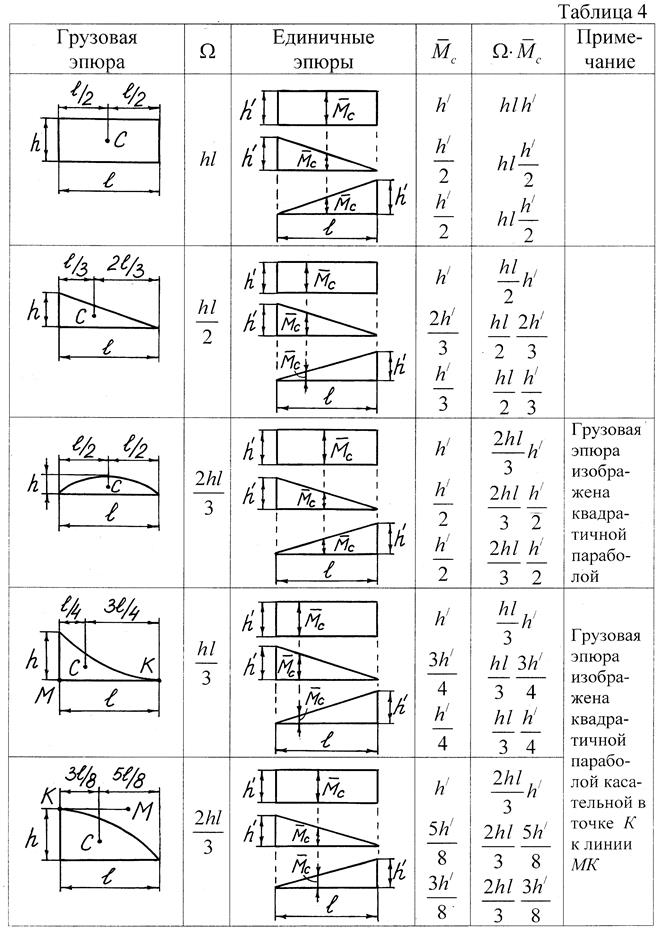
Если площадь грузовой эпюры и ордината под ее центром тяже­сти, взятая с единичной эпюры, расположены по разные стороны от базовой линии, то их произведение берется со знаком «минус». Фор­мулы для вычисления площадей (W) фигур, изображающих грузовые эпюры на участках, положение центров тяжести (С) этих фигур, а также соответствующие им ординаты (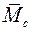) на единичных эпюрах для наиболее простых случаев даны в табл. 4.

В более сложных случаях перемножение эпюр на линейных участках (рис. 5) может быть выпол­нено по универсальной формуле

,*

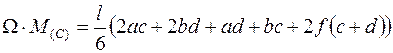(3.5)

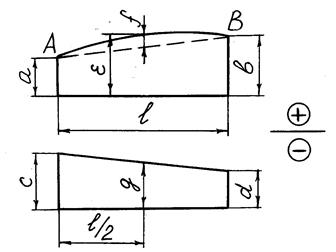
где l – длина участка; a, b – ординаты грузовой эпюры на границах участка; c, d – ординаты единичной эпюры на границах участка; f – высота параболического сегмента грузовой эпюры.

Ординаты a, b, c, d, f подставляются в формулу (3.5) с учетом знаков. Правило знаков для ординат устанавливает сам студент, на­пример так, как показано на рис. 5. Знак f берется по отношению к линии АВ. Ордината f считается положительной, если она направ­лена от линии АВ в сторону знака «плюс», и отрицательной, если в сторону знака «минус».

* Формула в таком виде предложена автором

	Грузовая эпюра Правило знаков
Единичная эпюра

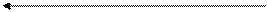
Рис. 5

Значение f для эпюр изгибающих моментов при наличии на участке равномерно распределенной нагрузки может быть опреде­лено так:

,

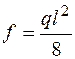(3.6)

где q – интенсивность равномерно распределенной нагрузки; l – длина участка.

Примечание. Если по формуле (3.5) перемножаются две эпюры, огра­ниченные прямыми линиями, то f = 0 и формула (3.5) превращается в известную формулу трапеций.

Известна и другая универсальная формула

,

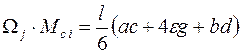(3.7)

где e, g – ординаты грузовой и единичных эпюр на середине участка.

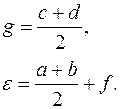
(3.8)

Ординаты e и g, так же как и ординаты a, b, c, d, f, в формулы (3.7) и (3.8)подставляют с учетом принятого правила знаков.

По формулам (3.5) и (3.7) могут перемножаться эпюры, изображае­мые треугольниками, прямоугольниками, трапециями, в том числе и перекрученными, в любом сочетании. Одна из перемножаемых эпюр может быть ограничена квадратичной параболой.

Дата добавления: 2015-06-30