Решение. Для рамы (рис. 8а) определить допускаемое значение интенсив­ности равномерно распределенной нагрузки [q]

Пример 2

Для рамы (рис. 8а) определить допускаемое значение интенсив­ности равномерно распределенной нагрузки [ q ].

Исходные данные: [s] = 160 МПа, M = ql², l = 3 м, поперечное сечение – двутавр № 20.

Расчетная схема рамы статически неопределима.

1. Раскрываем статическую неопределимость.

Определяем степень статической неопределимости.

L = C_о – C_н = 5 – 3 = 2.

Общее число связей C_о, наложенных на раму, равно 5 (три в опоре А и две в опоре В).

Так как рама плоская, то число связей, необходимых для ее равнове­сия, С_н = 3.

Рис. 8

Выбираем основную систему.

Для этого раму освобождаем от всей нагрузки и связей в опоре В. Полученная ОС дана на рис. 8б.

Переходим к эквивалентной системе.

Для этого ОС нагружаем заданной нагрузкой и неизвестными силами X₁, X₂ в точке В взамен отброшенных связей. Полученная таким образом ЭС дана на рис. 8в.

Записываем систему канонических уравнений.

Для дважды статически неопределимой стержневой системы она имеет вид

Вычисляем коэффициенты системы канонических уравнений.

Для этого строим грузовую М_р (рис. 8г) и единичные М₁ и М₂ (рис. 8д,е) эпюры.

Перемножая единичные эпюры по формуле (3.3а), вычисляем ко­эффициенты при неизвестных

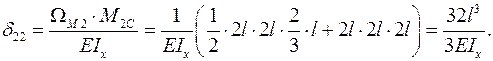
Перемножая грузовую эпюру с единичными по формуле (3.3а), вычисляем 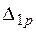и .

Примечание. получены со знаком «минус», так как перемно­жаемые эпюры лежат по разные стороны от базовой линии.

Решаем систему уравнений.

Все коэффициенты сокращаем на общий множитель l³/EI_x и под­ставляем в исходную систему уравнений.

Из второго уравнения выразим Х₁:

(*)

и подставим его в первое уравнение

.

Отсюда .

Найденное значение Х₂ подставляем в выражение (*) и находим Х₁.

.

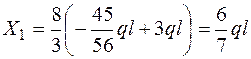Проверим правильность решения системы уравнений. Для этого Х₁ и Х₂ подставим в одно из уравнений исходной системы, например во второе

,

и убедимся, что система уравнений решена верно.

Строим суммарную эпюру изгибающих моментов М_сум.

Воспользуемся для этого способом сложения эпюр по формуле (3.12)

.

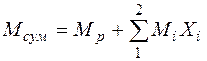Границы участков обозначим буквами А, В, С, D (рис. 8в). Будем счи­тать положительными ординаты эпюр, отложенные на горизонталь­ном стержне вверх, на вертикальном влево (рис. 9).

I участок

Точка В: М_сум = 0.

Точка D: М_сум = .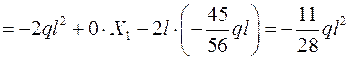

II участок

Точка D: М_сум = .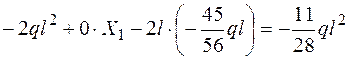

Точка С: М_сум = .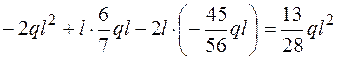

III участок:

Точка С: М_сум = .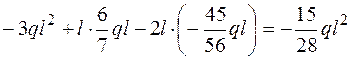

Точка А: М_сум = .

На участке I на эпюре М_сум возможен экстремум, так как здесь имеется равномерно распределенная нагрузка. Для выяснения этого изобразим схему нагружения участка (рис. 10), запишем выра­жение для Q и приравняем его нулю.

,

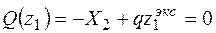откуда .

Так как находится внутри участка I, то на эпюре М_сум будет экстремум.

.

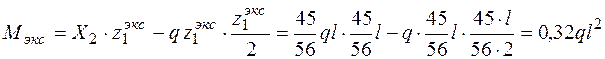Примечания:

1. Экстремум на эпюре М_х будет в том случае, если z^экс больше 0 и меньше длины участка.

2. При записи выражения для М_экс следует соблюдать принятое правило знаков. Если внешний силовой фактор (Р, М, q) изги­бает отсеченную часть относительно сечения в сторону знака «+», то момент от этого фактора записывают со знаком «+», иначе – со знаком «–».

По вычисленным значениям М_сум в соответствии с принятым правилом знаков строим эпюру М_сум (рис. 8ж).

Примечание. Студенты при выполнении контрольной работы могут строить эпюру М_сум любым способом.

Выполняем деформационную проверку.

Выбираем другую основную систему (что не обязательно, но желательно), убирая 2 связи в опоре А. Вместо отброшенной горизон­тальной связи прикладываем единичную силу . Строим от ее действия эпюру (рис. 8з). Эпюру М_сум перемножаем на эпюру 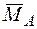по формуле (3.5):

.

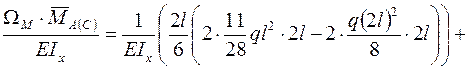
Итак, все действия по построению эпюры М_сум выполнены правильно.

3. Определяем [ q ].

Условие прочности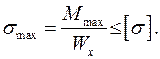

(взято с эпюры М_сум).

W_x = 184 см³ (по сортаменту для двутавра № 20).

Тогда

.

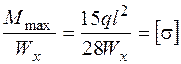Отсюда

Н/м =6,1 кН/м.

Дата добавления: 2015-06-30