Решение. Пример расчета (задача № 3)

Пример расчета (задача № 3)

Для сечения, составленного из швеллера №20 а, равнобокого уголка (80´80´8)×10^{-9 м3} и полосы (180´10)×10^{-6 м2} (рис. 3.6) требу­ется:

1. Найти общую площадь сечения;

2. Определить центр тяжести составного сечения;

3. Определить осевые и центробежный моменты инерции сече­ния относительно осей, проходящих через его центр тяжести;

4. Найти положение главных центральных осей инерции;

5. Определить величины главных центральных моментов инер­ции сечения и проверить правильность их вычисления;

6. Вычислить величины главных радиусов инерции.

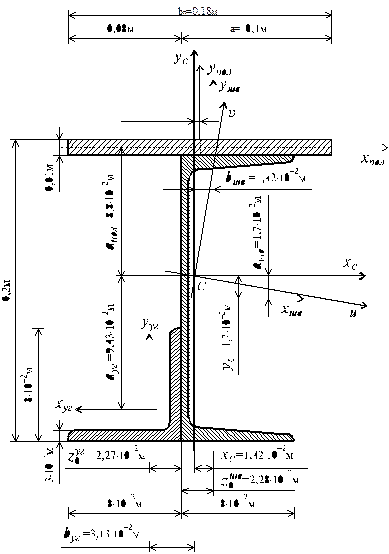
Рис. 3.6

Из сортамента выписываем все необходимые геометрические характеристики для профилей, входящих в составное сечение. Швеллер № 20 а (ГОСТ 8240-72): h_шв = 0,2 м, b_шв = 0,08 м, F_шв = 25,2×10^-4м², = 1670×10^-8м⁴, 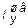= 139×10^-8м⁴, = 0,0228 м.

Уголок (80´80´8)×10^{-9 м3} (ГОСТ 8509-72): b_уг = 0,08 м, F_уг = = 12,3×10^{-4 м2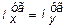}, = 73,4×10^-8 м⁴, 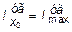= 116×10^-8 м⁴, 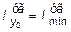=30,3×10^-8 м⁴, = 0,0227 м.

Полоса b_П ×d _П = 18×1×10^{-4 м2}, F_П = b_П ×d _П = 18×1×10^-4 м² = 18×10^{-4 м2};

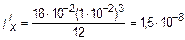м⁴, 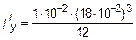= 486×10^-8 м⁴.

1. Определение общей площади составного сече­ния. Общая площадь составного сечения определяется по фор­муле:

F = F_шв + F_уг + F_П, F = (25,2 + 12,3+18)×10^-4 = 55,5×10^{-4 м2}.

2. Определить центр тяжести составного сече­ния. В качестве вспомогательных осей для определения положения центра тяжести примем горизонтальную и вертикальную оси x_шв и y_шв , проходящие через центр тяжести швеллера. Статические моменты площади всего сечения относительно этих осей будут равны:

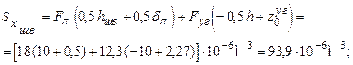
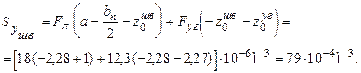
Координаты центра тяжести вычисляем по формулам:

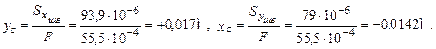
3. Определить осевые и центробежный моменты инерции сечения относительно осей, проходящих че­рез его центр тяжести. Для определения указанных момен­тов инерции составного сечения воспользуемся формулами, выра­жающими зависимость между моментами инерции относительно параллельных осей:

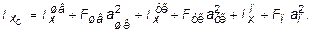(3.16)

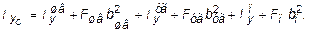(3.17)

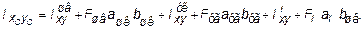(3.18)

В этих формулах расстояние между осями, проходящими через центр тяжести составного сечения, и осями, проходящими через центры тяжести каждой составной части фигуры, а и b (рис. 3.6), в рассматриваемом случае будут равны:

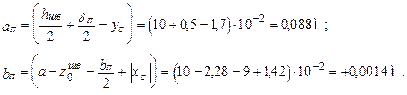
Подставив числовые значения величин в формулы (3.16) и (3.17), получим:

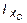= [1670 + 25,2(-1,7)² + 73,4 + 12,3(-9,43)² + 1,5 + 18×(8,8)²]×10^-8 = = 4305,4×10^-8 м⁴.

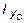= [139 + 25,2(1,42)² + 73,4 + 12,3(-3,13)² + 486 +18(0,14)²)×10^-8 = = 870,1×10^-8 м⁴.

При вычислении центробежного момента инерции составного сечения следует иметь в виду, что и 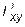равны 0, так как швеллер и полоса имеют оси симметрии, а

,

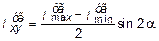где 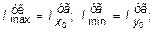a - угол между осью x и главной осью x ₀ уголка. Этот угол может быть положительным или отрицатель­ным. В нашем примере a = +45°, поэтому:

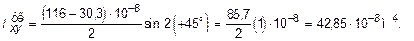
Далее, подставив числовые значения в формулу (3.18), получим величину центробежного момента инерции составного сечения:

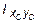= [0 + 25,2 × (-1,7) × 1,42 + 42,85 + 12,3 × (-9,43) (-3,13) + 0 +

+ 18 × 8,8 × 0,14] ×10^-8 = 367,2×10^-8 м⁴.

4. Найти положение главных центральных осей инерции. Угол наклона главных осей инерции, проходящих через центр тяжести составного сечения, к центральным осям инерции x_C и y_C определим по формуле:

.

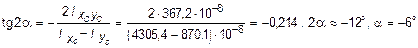Так как угол a получился отрицательным, то для отыскания по­ложения главной оси максимального момента инерции u следует ось x ₀, осевой момент инерции относительно которой имеет наи­большее значение, повернуть на угол a по ходу часовой стрелки. Вторая ось минимального момента инерции v будет перпендику­лярна оси u.

5. Определить величины главных центральных мо­ментов инерции сечения и проверить правильность их вычисления. Величины главных центральных моментов инерции составного сечения вычисляем по формуле:

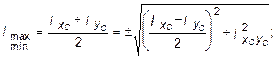
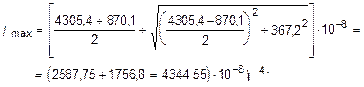
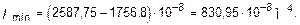
Для контроля правильности вычисления величины моментов инерции составного сечения производим проверки.

1-ая проверка: I _max + I _min = 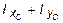= const;

I _max + I _min = (4344,55 + 830,95)×10^-8 = (5175,5)×10^-8 м⁴;

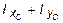= (4305,4 + 870,1)×10^-8 = (5175,5)×10^-8 м⁴.

2-ая проверка: I _max > 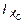> > 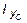0;

4344,55 ×10^-8 > 4305,4×10^-8 > 870,1×10^-8 > 830,95×10^-8 м⁴.

Проверки удовлетворяются, что говорит о правильности вычис­ления моментов инерции составного сечения.

6. Вычислить величины главных радиусов инерции. Величины главных радиусов инерции вычисляем по известным формулам:

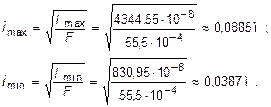
Дата добавления: 2015-06-30