Внутренние усилия в поперечных сечениях бруса

ИЗГИБ

Пример расчета (задача 5)

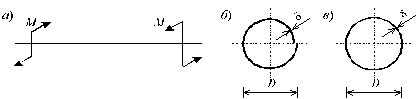
Пусть задан тонкостенный стержень (рис. 4.10, а) при действии самоуравновешивающих крутящих моментов на двух противопо­ложных концах, требуется:

1. Определить выражения максимальных напряжений и углов закручивания в случаях, когда стержень имеет открытый (рис. 4.10, б) и замкнутый (рис. 4.10, в) профиль;

2. Сопоставить вычисленные значения напряжений и углов за­кручивания для двух различных профилей тонкостенного стержня.

Решение

1. Определение выражения максимальных напряже­ний и углов закручивания в случаях, когда стержень имеет открытый и замкнутый профиль. Для стержня с открытым профилем (рис. 4.10, б), согласно (4.17), получим:

; .

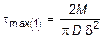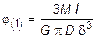Рис. 4.10

Для стержня замкнутого профиля (рис. 4.10, в), воспользовав­шись выражениями (4.22) и (4.25), имеем:

; .

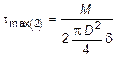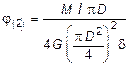2. Сопоставить вычисленные значения напряжений и углов за­кручивания для двух различных профилей тонкостенного стержня. Для наглядности составим отношения выражений напряжений и углов закручивания, т.е.:

; .

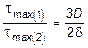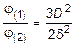Откуда следует, что отношение напряжений имеет величину порядка D /d, а отношение углов закручивания - порядка (D /d)². Так как для тонкостенных стержней D >>d, следовательно, стер­жень с замкнутым профилем является существенно более прочным и жестким, нежели стержень с открытым профилем при идентич­ных исходных данных.

Заметим, что этот вывод является общим для тонкостенных стержней независимо от формы сечений.

Под изгибом понимается такой вид нагружения, при котором в поперечных сечениях бруса возникают изгибающие моменты M_x или M_y. Если изгибающий момент в сечении является единст­венным силовым фактором, то изгиб называется чистым (рис. 5.1, а).

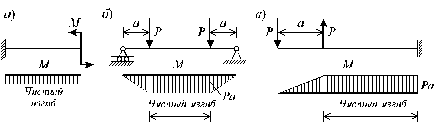
Рис. 5.1

В тех случаях, когда в поперечных сечениях бруса наряду с изгибающим моментом возникают и поперечные силы изгиб назы­вается поперечным. Брус, работающий в основном на изгиб, часто называют балкой. В дальнейшем будем рассматривать такие случаи изгиба балки, при которых, во-первых, поперечное сечение балки имеет хотя бы одну ось симметрии, и, во-вторых, вся нагруз­ка лежит в плоскости, совпадающей с осью симметрии балки. Та­ким образом, одна из главных осей инерции лежит в плоскости изгиба, а другая перпендикулярна ей.

Для того, чтобы правильно ориентироваться в вопросах, связан­ных с расчетом бруса на изгиб, необходимо прежде всего научиться определять законы изменения внутренних силовых факторов, т.е. научиться строить эпюры изгибающих моментов и поперечных сил.

Предварительно рассмотрим три основных типа опорных связей балки с основанием:

1. Шарнирно-подвижная опора (рис. 5.1, б - левая опора бал­ки), ограничивающая лишь вертикальное перемещение опорного узла.

2. Шарнирно-неподвижная опора (рис. 5.1, б - правая опора балки), ограничивающая вертикальное и горизонтальное перемеще­ния опоры.

3. Жесткая заделка (рис. 5.1, а - опора балки на левом краю), не допускающая поворота и перемещений по вертикали и горизон­тали сечения балки, примыкающего к опоре.

По запрещенным направлениям во всех этих типах опор воз­никают соответствующие реакции.

Рассмотрим характерный пример (рис. 5.2, а) и установим не­обходимые правила. Решение задачи, как правило, начинается с определения полной системы внешних сил. Для этого отбросим опоры и заменим их соответствующими реакциями (рис. 5.2, б), выполняющими ту же роль, что и опорные закрепления.

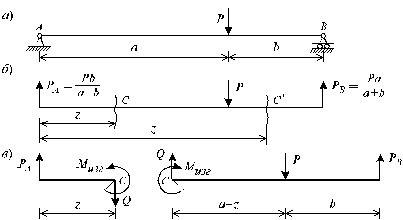
Рис. 5.2

Заданная система статически определима, следовательно, из ус­ловий равновесия системы, т.е. равенства нулю суммы моментов всех сил относительно шарнирных опор (в шарнирах нет ограниче­ний поворота сечений балки, поэтому изгибающих моментов не возникает) S m (A) = 0 и S m (В) = 0, определяем вертикальные реакции в опорах:

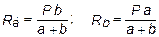. (5.1)

Для определения Н_А имеем: 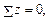откуда Н_А =0. Для проверки правильности вычислений воспользуемся усло­вием равенства нулю суммы всех вертикальных сил S y = 0, откуда получим

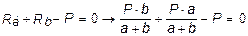, 0 = 0.

Для определения внутренних силовых факторов - изгибающего момента М (z) и поперечной силы Q (z) как функций от продоль­ной координаты z, воспользуемся методом сечений. Для полу­чения этих зависимостей балку разбивают на участки, границами которых являются следующие точки: начало и конец балки; точки приложения сосредоточенных усилий; начало и конец действия распределенных усилий; сечения, в которых скачкообразно изменя­ется жесткость балки; в точках, где происходит изменение ориен­тации элементов, если имеем дело с стержневой системой со сложной структурой.

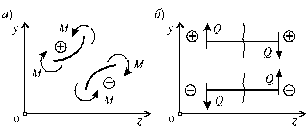Рис. 5.3

Заданная система состоит из двух участков - первого (0 £ z £ a) и второго (a £ z £ a + b). Следовательно, задавая последовательно сечения, принадлежащие к первому и второму участкам, и рассмат­ривая равновесие отсеченных частей системы при действии на них всех внешних сил и внутренних уси­лий, определим выражения для внутренних сило­вых факторов. При этом, знак изгибающего мо­мента устанавли­вается по знаку кривизны изогну­того бруса (рис. 5.3, а) и зависит от выбранного направления осей системы координат y 0 z. Следовательно, в системе координат y 0 z принятой на рис. 5.3, а положительный момент вызывает рас­тяжение нижних волокон балки.

Для поперечных сил, независимо от направления координатных осей, устанавливается следующее правило знаков: если результиру­ющая поперечная сила Q_y вращает рассматриваемую часть балки по ходу часовой стрелки, то она считается положительной, в обратном случае - отрицательной (рис. 5.3, б).

Из условия равновесия S M_x = 0; S y = 0 отсеченной части системы, расположенной левее от сечения z ₁ (первый участок), (см. рис. 5.2, в), получим:

M_x (z ₁) = R_{a ×}z ₁; Q_y = R_a. (5.2)

Для определения M_x и Q_y на втором участке рассмотрим рав­новесие отсеченной части балки, расположенной правее от сечения z ₂ (см. рис. 5.2, б), т.е. S M_x = 0; S y = 0 откуда и определим:

M_x (z ₂) = R_b (a + b - z ₂); Q_y = - R_b . (5.3)

Эпюры M_x и Q_y изображены на рис. 5.4. Заметим, что эпюры изгибающих моментов M_x , как и поперечных сил Q_y строятся на оси бруса, однако в отличие от эпюры поперечных сил знак момента не указывается, а ординаты изгибающего момента откла­дываются co стороны растянутых волокон.

Рис. 5.4

5.2. Основные дифференциальные соотношения
теории изгиба

Пусть брус нагружен произвольным образом распределенной нагрузкой q = f (z) (рис. 5.5, а).

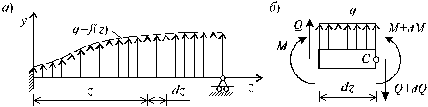
Рис. 5.5

Выделим из бруса элемент длиной dz и приложим по его краям положительные внутренние усилия (рис. 5.5, б). В пределах малого отрезка dz нагрузку q можно считать распределенной равномерно. Приравняем нулю сумму проекций всех сил на вертикальную ось y и сумму моментов всех сил относительно поперечной оси x, прохо­дящей через точку С (рис. 5.5, б), получим:

Q_y + q dz - Q_y - d Q_y = 0;

M_x + Q_y dz + q dz × dz /2 - M_x - d M_x = 0.

Производя упрощения и отбрасывая величины высшего поряд­ка малости, получим:

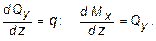(5.4)

откуда

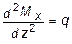. (5.5)

Из (5.4) следует, что при q = const функция Q_y будет линей­ной, а функция M_x - квадратичной. Если на каких-то участках бруса распределенная нагрузка отсутствует, т.е. q = 0, то получим, что Q_y = const, а M_x является линейной функцией от z.

В сечениях, где приложена сосредоточенная сила, эпюра Q_y претерпевает скачок на величину внешней силы. И наконец, в тех сечениях, где Q_y принимает нулевое значение и меняет знак, функция M_x достигает экстремальных значений.

Дата добавления: 2015-06-30