Касательные напряжения при поперечном изгибе. Главные напряжения при изгибе 2 страница

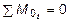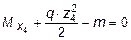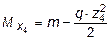, , - (парабола).

В граничных сечениях D и В участка IV ординаты эпюр Q_y и M_x :

при z ₄ 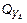= 0 = 0, 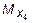= 20 кН×м;

при z ₄ = 1 м 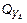= 20×1 =20 кН, 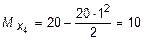кН×м.

Так как величина 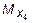на участке IV изменяется по закону квадратной параболы, то для уточнения ее очертания надо опреде­лить ординату эпюры M_x в каком-нибудь промежуточном сечении. Например, при z ₄ = 0,5 м, где ордината 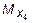будет равна:

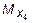
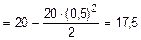кН×м.

Построение эпюр Q_y и M_x для всей балки

Откладывая перпендикулярно от оси абсцисс в удобном для пользования масштабе значения Q_y и M_x , возникающие в харак­терных и промежуточных сечениях каждого участка, и соединяя концы полученных ординат линиями, соответствующими законам изменения Q_y и M_x на этих участках, строим эпюры Q_y и M_x для всей балки (рис. 5.13, в, г).

2.1. Руководствуясь эпюрой M_x показать приблизи­тельный вид изогнутой оси балки. Анализируя эпюру M_x (рис. 5.13, г) видим, что на участке КО растянуты верхние волокна, и поэтому на этом участке изогнутая ось балки будет иметь вы­пуклость вверх. На участке ОD растянуты нижние волокна, и изо­гнутая ось балки будет иметь выпуклость вниз. Вследствие этого под т. О, где M_x = 0, будет точка перегиба. Учитывая все сказанное и то, что прогибы в опорных сечениях равны нулю, строим при­близительный вид изогнутой балки (рис. 5.13, д).

2.2. Подбор поперечного сечения балки. Опасным явля­ется сечение Е, где возникает наибольший по абсолютной величи­не M _max = 72,5 кН×м. Двутавровое сечение балки подбираем из ус­ловия прочности при изгибе при расчетном сопротивлении мате­риала R_H = 200×10³ кН/м² (сталь):

.

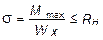Откуда требуемый момент сопротивления W_x равен:

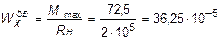м³ .

По сортаменту (ГОСТ 8239-72) принимаем двутавр № 27 с W_x = 37,1×10^-5 м³. В этом случае при проверке прочности получа­ется недонапряжение, но оно будет меньше 5%, что допускается СНиП при практических расчетах.

Заданная плоская стержневая система (рис. 5.17, а), элементы которой представляют собой прямолинейные стержни, жестко сое­диненных между собой, называется рамой. При произвольном характере нагружения, в поперечных сечениях элементов заданной системы возникают следующие три силовых фактора: поперечная сила Q, изгибающий момент M и продольная сила N. Главной от­личительной особенностью рамной системы от других стержневых систем является то, что в деформированной состоянии угол сопря­жения между различными элементами равен углам сопряжения элементов до нагружения системы.

Правило знаков для Q_y , M_x и N_z и порядок построения их эпюр для таких систем остаются прежними.

Так как заданная система имеет только три внешние связи (вертикальную и горизонтальную в т. D и горизонтальную в т. А), следовательно, при общем характере нагружения возникает всего три опорные реакции. Как нам уже известно, для плоских систем можно воспользоваться только тремя уравнениями равновесия ста­тики для определения опорных реакций, поэтому заданная система является статически определимой.

Рис. 5.17

Построить эпюры Q_y, M_x и N_z.

Определение опорных реакций. Составив уравнения равновесия для всей рамы и решив их, получим:

S y = 0, R_D = 0;

S M_D = 0, - H_A ×8 + Р ×4 + q ×4×2 = 0, кН;

S M_A = 0, H_D ×8 - Р ×4 - q ×4×6 = 0, 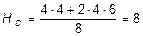кН.

Проверка: S x = 0; H_A + H_D - Р - q ×4 = 0;

4 + 8 - 4 - 2×4 = 0; 12 - 12 = 0; 0 = 0.

Уравнение равновесия превращается в тождество, что говорит о правильности вычисления опорных реакций.

Определение количества участков

Так как, в рамах границами участков являются точки приложе­ния сил и точки изменения направления оси элементов системы, то заданная система имеет три участка: участок I - АВ, участок II - ВС, участок III - СD (рис. 5.13, б).

Составление аналитических выражений Q_y, M_x и N_z и оп­ределение их значений в характерных сечениях каждого участка

Определение внутренних силовых факторов в сечениях рам производится также с помощью метода сечений. Однако при вы­полнении разрезов всегда следует выяснить, какую из частей рамы считать левой, а какую правой. Для этого предполагают, что обход рамы ведется слева направо, т.е. от А к В, от В к С, от С к D. При этом наблюдение ведут с нижней стороны участков, находясь ли­цом к оси участков.

Участок I (0 £ z ₁ £ 4 м) (рис. 5.18).

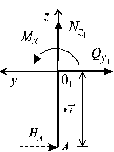Рис. 5.18

Проведя сечение в пределах этого участка, рассмотрим равновесие левой отсеченной час­ти длиной z ₁ . Составив уравнение равновесия S y = 0 и 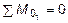и S z = 0 для этой части и решив их относительно , 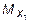и 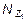, полу­чим аналитические выражения изменения Q_y , M_x и N_z на участке I:

S y = 0, - H_A - =0, = - H_A - const;

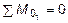, - H_A × z ₁ - 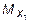= 0, 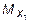= - H_A × z ₁ -уравнение прямой;

S z = 0, 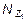= 0 - нормальная сила отсутствует.

Величины Q_y , M_x и N_z в граничных сечениях участка будут равны:

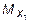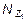при z ₁ = 0 = -4 кН, = 0, = 0;

при z ₁ = 4 м = -4 кН, 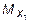= -4×4 = -16кН×м, 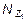= 0.

Участок II (0 £ z ₂ £ 4 м) (рис. 5.19).

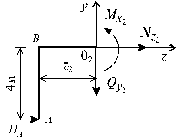Рис. 5.19

Сделав сечение в пределах этого участка, составим уравнения равнове­сия для левой части:

S y 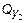= 0, = 0;

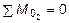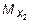, - - H_A ×4 = 0,
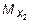= - H_A ×4 = -4×4 = -16 кН×м;

S z = 0, H_A + 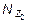= 0, 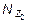= - H_A = -4 кH.

Знак “минус” перед 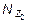говорит о том, что элемент ВС сжат, а не растянут. Из полученных уравнений видно, что на участке II по­перечная сила равна нулю, а изгибающий момент и нормальная сила постоянны.

Участок III (0 £ z ₃ £ 4 м) (рис. 5.20). Приняв начало координат в сечении D и сделав разрез в пределах этого участка, рассмотрим равновесие правой отсеченной части длиной z ₃ . Составив урав­нения равновесия S y = 0; 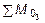= 0 и S z = 0 и решив их, полу­чим:

Рис. 5.20

S y = 0, - H_D + q × z ₃ = 0,
= H_D - q × z ₃ - уравнение прямой.

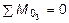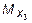, + H_D × z ₃ - ,

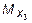= - H_D × z ₃ + - уравнение квадрат­ной параболы;

S z = 0, N_z = 0.

Ординаты эпюр найдем из полученных выражений, подставив в них значения z ₃, соответствующие граничным сечениям участка:

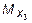при z ₃ = 0 = 8 кН, = 0, = 0;

при z ₃ = 4 м = 8 - 2×4 =0, 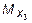= -8×4 + = -16 кН×м, = 0.

Для уточнения очертания квадратной параболы определим величину 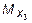при z ₃ = 2 м:

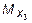
кН×м.

Построение эпюр Q_y , M_x и N_z для бруса с ломанной осью (рамы)

Отложив в масштабе перпендикулярно к оси каждого элемента рамы полученные значения Q_y, M_x, N_z в граничных и проме­жуточных сечениях участка и соединяя концы ординат линиями, соответствующими выражениям Q_y, M_x и N_z , строим их эпюры (рис. 5.17, в, г, д).

Правильность построения эпюр внутренних усилий подтверж­дается на основе статической проверки, заключающейся в том, что условия равновесия рамы (S x º 0; S y º 0; S M º 0;), как в целом, так и любой ее отсеченной части, под воздействием внешних нагрузок и усилий, возникающих в проведенных сечениях, соблюдаются тождественно.

В случае поперечного изгиба в сечениях балки возникают не только изгибающий момент, но и поперечная сила. Следовательно, в этом случае в поперечных сечениях бруса возникают не только нормальные, но и касательные напряжения.

Так как касательные напряжения в общем случае распределены по сечению неравномерно, то при поперечном изгибе поперечные сечения балки строго говоря не остаются плоскими. Однако при 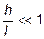(где h - высота поперечного сечения, l - длина балки) ока­зывается, что эти искажения заметным образом не сказываются на работе балки на изгиб. В данном случае гипотеза плос­ких сечений и в случае чистого изгиба с достаточной точно­стью приемлема. Поэтому для расчета нормальных напряже­ний s применяют ту же формулу (5.10).

Рассмотрим вывод расчетных формул для касательных напря­жений. Выделим из бруса, испытывающего поперечный изгиб, элемент длиной dz (рис. 5.21, а).

Рис. 5.21

Продольным горизонтальным сечением, проведенным на рас­стоянии y от нейтральной оси, разделим элемент на две части (рис. 5.21, в) и рассмотрим равновесие верхней части, имеющей основание шириной b. При этом с учетом закона парности каса­тельных напряжений, получим, что касательные напряжения в по­перечном сечении равны касательным напряжениям, возникающим в продольных сечениях (рис. 5.21, б). С учетом данного обстоятель­ства и из допущения о том, что касательные напряжения по пло­щади b × dz распределены равномерно, используя условие å z = 0, получим:

N ^* - N ^* - d N ^* + t× b × dz = 0,

откуда

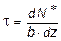. (5.12)

где N ^* - равнодействующая нормальных сил s× dF в левом попереч­ном сечении элемента dz в пределах заштрихованной площади F ^* (рис. 5.20, г):

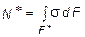. (5.13)

С учетом (5.10) последнее выражение можно представить в виде

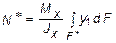, (5.14)

где 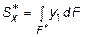- статический момент части поперечного сечения, расположенной выше координаты y (на рис. 5.21,б эта область за­штрихована). Следовательно, (5.14) можно переписать в виде

,

откуда

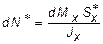. (5.15)

В результате совместного рассмотрения (5.12) и (5.15) получим

,

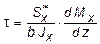или окончательно

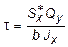. (5.16)

Полученная формула (5.16) носит имя русского ученого Д.И. Журавского.

Для исследования напряженного состояния в произвольной точке балки, испытывающей поперечный изгиб, выделим из сос­тава балки вокруг исследуемой точки элементарную призму (рис. 5.21, г), таким образом, чтобы вертикальная площадка явля­лась частью поперечного сечения балки, а наклонная площадка составляла произвольный угол a относительно горизонта. Прини­маем, что выделенный элемент имеет следующие размеры по координатным осям: по продольно оси - dz, т.е. по оси z; по вер­тикальной оси - dy, т.е. по оси у; по оси х - равный ширине балки.

Так как вертикальная площадка выделенного элемента принад­лежит поперечному сечению балки, испытывающему поперечный изгиб, то нормальные напряжения s на этой площадке определя­ются по формуле (5.10), а касательные напряжения t - по формуле Д.И. Журавского (5.16). С учетом закона парности касательных на­пряжений, легко установить, что касательные напряжения на гори­зонтальной площадке также равны t. Нормальные же напряжения на этой площадке равны нулю, согласно уже известной нам гипо­тезе теории изгиба о том, что продольные слои не оказывают дав­ления друг на друга.

Обозначим величины нормальных и касательных напряжений на наклонной площадке через s_a и t_a, соответственно. Принимая площадь наклонной площадки dF, для вертикальной и горизон­тальной площадок будем иметь dF sin a и dF cos a, соответственно.

Составляя уравнения равновесия для элементарной вырезанной призмы (рис. 5.21, г), получим:

,

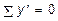откуда будем иметь:

;

.

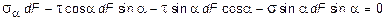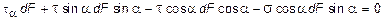Следовательно, окончательные выражения напряжений на на­клонной площадке принимают вид:

Определим ориентацию площадки, т.е. значение a = a₀, при котором напряжение s_a принимает экстремальное значение. Со­гласно правилу определения экстремумов функций из математиче­ского анализа, возьмем производную функции s_a от a и прирав­няем ее нулю:

.

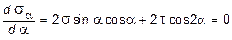Предполагая a = a₀, получим:

.

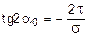Откуда окончательно будем иметь:

.

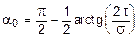Согласно последнему выражению, экстремальные напряжения возникают на двух взаимно перпендикулярных площадках, называ­емых главными, а сами напряжения - главными напряже­ниями.

Сопоставляя выражения t_a и 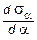, имеем:

,

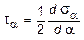откуда и следует, что касательные напряжения на главных пло­щадках всегда равны нулю.

В заключение, с учетом известных тригонометрических тож­деств:

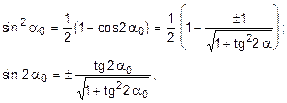
и формулы ,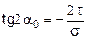

определим главные напряжения, выражая из через s и t:

.

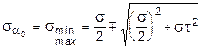Полученное выражение имеет важное значение в теории проч­ности изгибаемых элементов, позволяющее производить расчеты их прочности, с учетом сложного напряженного состояния, присущее поперечному изгибу.

Дата добавления: 2015-06-30