Тема 2.2. Растяжение и сжатие

Вопросы для самопроверки.

1. Каковы задачи сопротивления материалов?

2. В чем различие между упругими и пластическими деформа­циями?

3. Что называют прочностью, жесткостью, устойчивостью детали?

4. В чем различие между брусом, оболочкой, массивом?

5. Как классифицируют внешние силы?

6. Какие допущения о свойствах материалов и характере дефор­маций приняты в сопротивлении материалов?

7. Как выбрать расчетную схему элемента конструкции?

8. В чем заключается метод сечений?

9. Что представляют собой внутренние силовые факторы?

10. Какие возможны виды деформации тела и как они связаны с внутренними силовыми факторами?

11. Что представляет собой напряжение в точке? В каких едини­цах его измеряют?

12. Почему, говоря о напряжении в точке, необходимо указывать ориентацию секущей плоскости?

13. Какое напряжение называют нормальным, какое — касатель­ным?

14. Как связаны напряжения в сечении с внутренними силовыми факторами?

15. Каковы признаки нарушения прочности детали?

16. Что такое коэффициент запаса прочности? Что такое требуемый коэффициент запаса прочности?

17. Какие напряжения называются предельными? Что такое допускаемое напряжение, расчётное напряжение? От каких факторов они зависят?

18. Как изменится вес конструкции, если её выполнить с меньшим запасом прочности?

19. В чём различие между деформациями и перемещениями?

20 Как составляют условие жёсткости для элементов конструкций?

21. Что следует понимать под напряжённым состоянием в точке?

Растяжение и сжатие. Внутренние силовые факторы при растяжении и сжатии.

Эпюры продольных сил.

Напряжения в поперечных сечениях бруса при растяжении и сжатии.

2.2.4. Эпюры нормальных напряжений.

Деформации и перемещения при растяжении и сжатии.

Механические свойства материалов и их характеристики. Испытания материалов на растяжение (сжатие).

2.2.7. Расчёты на прочность и жёсткость при растяжении и сжатии.

2.2.1. Растяжением или сжатием называют такой вид деформации бруса (стержня), при котором в его поперечных сечениях возникает только продольная сила N.

Продольной силой в поперечном сечении бруса называется равнодействующая внутренних нормальных сил, возникающих в этом сечении.

При сжатии сравнительно длинного и тонкого бруса прямолинейная форма его равновесия может оказаться неустойчивой. В этой теме будем во всех случаях полагать, что опасность потери устойчивости исключена. Расчёты на устойчивость будут рассмотрены в теме 2.10.

Продольную силу определяют методом сечений и уравнение (2.1.1.) позволяет сформулировать правило определения продольной силы: продольная сила в произвольном поперечном сечении бруса численно равна алгебраической сумме проекций на ось z, направленную по нормали к сечению, всех внешних сил, приложенных к рассматриваемой части бруса. Заметим, что продольная сила, возникающая в проведенном сечении, принадлежащем рассматриваемой части, равна по модулю и противоположна по направлению силе, возникающей в том же сечении, но принадлежащем отброшенной части.

Внутренние силовые факторы могут иметь направления, показанные на рис. 2.1.6 Били противоположные им. В за­висимости от их направления им приписывают знак плюс или минус.

Продольная сила N считается положительной, если она направлена от сечения в сторону внешней нормали, т. е. по отношению к рассматриваемой части бруса она является растягивающей (рис. 2.2.1.). В противном случае ей приписы­вают знак минус.

При решении задач знак N удобнее устанавливать в за­висимости от направления внешних сил: внешняя сила, на­правленная в сторону, противоположную направлению внешней нормали к сечению, вызывает в нем положитель­ную продольную силу, а внешняя сила, направление кото­рой совпадает с направлением внешней нормали к сечению, вызывает в нем отрицательную нормальную силу.

Например, применяя это правило к брусу на рис. 2.2.2. А и рассматривая левую отсеченную часть (рис. 2.2.2. Б), заключаем, что сила 1Н, направление которой противоположно направлению внешней нормали к рассматриваемому сечению 1—1, вызывает в нем положительную нормальную силу, а сила 5 Н, направление которой совпадает с направлением внешней нормали, вызывает отрицательную нормальную силу. Таким образом, в сечении 1—1возникает нормальная сила N=1Н - 5Н= - 4Н. Если рассматривать правую отсеченную часть бруса (рис. 2.2.2. В), то получим тот же результат N=- 3Н – 1Н = - 4Н.

2.2.2. Очевидно, значения внутренних силовых факторов в раз­личных сечениях одного и того же бруса различны. Графи­ки, показывающие, как изменяются внутренние силовые факторы вдоль оси бруса, называют эпюрами внутренних силовых факторов. Эпюры строят в первую очередь для того, чтобы использовать их при расчете бруса на прочность; они дают возможность найти наибольшие значения внутрен­них силовых факторов и положение сечений, в которых они возникают. Эти сечения для бруса постоянного поперечного сечения являются опасными.

Методику построения эпюр продольных сил рассмотрим на конкретных примерах.

Пример 1. Построить эпюру продольных сил для бруса (рис. 2.2.3), нагружен­ного в сечениях А, В, С сосредоточенными силами , , , направленными вдоль оси.

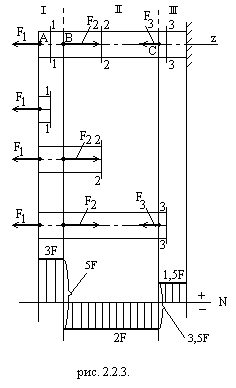Решение. Разобьём брус на 3 участка (границами участков нагружения являются сечения, в которых приложены внешние нагрузки).

Применяя метод сечений, мысленно на участке 1 (АВ)рассекаем брус произвольным поперечным сечением 1-1, отбрасываем правую часть (это позволяет не определять реакцию задел­ки) и рассматриваем левую оставленную часть. Согласно принятому правилу знаков . Очевидно, что нор­мальная сила 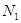во всех сечениях участка одинакова, а ос­тальные внутренние силовые факторы в этих сечениях от­сутствуют.

Проводя сечение 2-2 на участке 11 (ВС) и рассматривая левую часть бруса, получаем . Аналогично определяем нормальную силу в произвольном се­чении 3—3участка 111 (CD): .

Очевидно, что в пределах каждого из рассмотренных уча­стков нормальная сила постоянна. Участок бруса, в пределах которого внутренние силовые факторы изменяются по единому закону, называют участ­ком нагружения.

Для построения эпюры N (рис. 2.2.3.) параллельно оси бруса проводим ось абсцисс графика (ось эпюры). Значения нормальных сил, подсчитанные в рассмотренных сечениях, откладываем в выбранном мас­штабе и с учетом их знаков от оси эпюры под соответст­вующим сечением бруса, а затем через эти ординаты в пре­делах каждого участка проводим линии параллельно оси абсцисс. Принято ось эпюры проводить тонкой, а саму эпюру толстой линиями. Эпюру штрихуют перпендикулярно оси эпюры — каждая линия штриховки (ордината графика) дает в принятом масштабе значение нормальной силы в соответствующем поперечном сечении бруса.

В местах приложения сосредоточенных сил на эпюре получаются скачкообразные изменения ординат – «скачки». Размер «скачка» равен приложенной в соответствующем месте бруса внешней сосредоточенной силе (см. рис. 2.2.3.). При нагружении бруса сосредоточенными силами эпюра N всегда имеет такой характер, как в рассмотренном примере.

Скачкообразное изменение ординат эпюры N носят условный характер, так как условно и само понятие «сосредоточенная сила». Фактически внешняя сила распределена по некоторой небольшой части длины бруса; в пределах этой части значение N изменяется (например, в зоне приложения силы 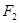от значения 3F до - 2F) по некоторому закону, установить который не представляется возможным. Неизвестный криволинейный переходный участок эпюры заменяют условным «скачком».

Пример 2. Построить эпюру нормальных сил для сво­бодно подвешенного бруса, нагруженного силами собствен­ного веса (рис. 2.2.4.). Длина бруса l, площадь поперечного сечения А, удельный вес материала .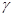

Решение. В заданном брусе один участок АВ, нагруженный равномерно распределёнными по его силами. Применяя метод сечений, мысленно рассекаем брус произвольным поперечным сечением 1-1 на расстоянии z от свободного конца бруса. Нормальная сила в этом сечении равна весу нижележащей части бруса: 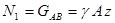. Следовательно, продольная сила пропорциональна z, т.е. ихменяется вдоль оси бруса по линейному закону. Для построения эпюры N вычисляем значения нормальных сил в сечениях А и В: 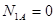, поскольку 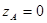и . Продольная сила при переходе от сечения к сечению изменяется непрерывно, а не скачкообразно, как это имеет место при действии ряда сосредоточенных сил.

Сечения, в которых приложены сосредоточенные нагрузки или которые определяют начало и конец распределённой нагрузки, называют характерными.

2.2.3. При растяжении (сжатии) бруса в его поперечных сечениях возникают только нормальные напряжения .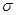

Продольную силу считают условно сосредоточенной в центре тяжести сечения. В действительности, как показано в п. 2.1.4., продольная сила представляет собой равнодействующую элементарных внутренних сил 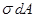, непрерывно распределённых по сечению: . (2.2.1.)

Для определения нормальных напряжений при известной продольной силе N и площади поперечного сечения А необ­ходимо знать закон распределения напряжений по сечению.

Нанесем на боковую поверхность стержня (для большей наглядности изготовленного из резины) сетку из линий, па­раллельных и перпендикулярных его оси. При растяжении стержня все продольные и поперечные линии остаются прямыми и взаимно перпендикулярными, расстояние между поперечными линиями увеличивается, а между продольными — уменьшается. Этот при­мер подтверждает гипотезу плоских сечений (гипотезу Бернулли): сечения стержня, плоские и перпендикулярные к его оси до деформации, остаются плоскими и перпендикулярными к оси и после деформации.

Если представить стержень состоящим из отдельных тон­ких продольных волокон, то на основании гипотезы плоских сечений и с учетом того, что сечения перемещаются парал­лельно самим себе, можно заключить, что все волокна удли­няются на одну величину, а значит, в них действуют одина­ковые по интенсивности внутренние силы, т. е. напряжения при растяжении (сжатии) распределены по сечению стерж­ня равномерно.

Вынесем постоянное нормальное напряжение 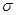в выра­жении (2.2.1.) за знак интеграла:

.

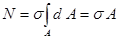Тогда получим . (2.2.2.)

Для нормальных напряжений принимают то же правило знаков, что и для продольных сил.

В сечениях, близких к месту приложения внешних сил, гипотеза Бернулли нарушается: сечения искривляются, и на­пряжения в них распределяются неравномерно. По мере удале­ния от сечений, в которых приложены силы, напряжения выравниваются, и в сечениях, удаленных от места приложения сил на расстояние, равное наибольшему из размеров по­перечного сечения, напряжения можно считать распределен­ными по сечению равномерно. Это положение, называемое принципом Сен-Венана, позволяет при определении напряже­ний в сечениях, достаточно удаленных от мест приложения внешних сил, не учитывать способ их приложения, заме­нять систему внешних сил статически эквивалентной систе­мой.

2.2.4. Если площадь поперечного сечения стержня непостоянна по его длине, то различны и напряжения. В этом случае для определения наиболее напряженного сечения недостаточно иметь эпюру продольных сил, необходимо построить эпюру нормальных напряжений, показывающую закон их изменения по длине бруса в виде графика. Рассмотрим ее построение на примере.

Пример 3. Для стержня со ступенчато – переменным поперечным сечением построить эпюры продольных сил и нормальных напряжений, если .

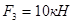
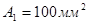
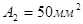Решение. Разбиваем стержень на участки, границами которых служат сечения, в которых приложены внешние силы, или ступенчато изменяется их площадь. Применяя метод сечений, определяем продольные силы в поперечных сечениях стержня: , , 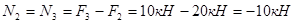. Строим эпюру продольных сил (рис. 2.2.5.).

Определяем нормальные напряжения на каждом участке по формуле (2.2.2.), подставив в неё значение сил (в Н) и площадей (в ):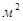

;

;

;

.

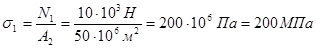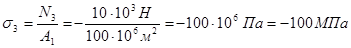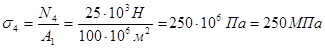В пределах каждого участка напряжение одинаково, так как одинаковы во всех сечениях значения продольной силы и площади поперечного сечения. Эпюра 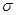на каждом участке – прямая, параллельная оси абсцисс.

2.2.5. Рассмотренный в п. 2.2.4. вопрос об опреде­лении нормальных напряжений теснейшим образом связан с расчетами бруса и шарнирно-стержневых систем на прочность. Умение вычислять деформации и переме­щения необходимо для расчетов на жесткость.

При растяжении стержня его длина увеличивается, а размеры поперечного сечения уменьшаются (рис. 2.2.6.), при сжатии наоборот.

Изменение длины стержня 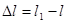называют линейной продольной деформацией (абсолютным удлинением); изменение размеров поперечного сечения 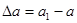- линейной поперечной деформацией.

Интенсивность деформирования оценивают деформациями, приходящимися на единицу длины (размер сечения) стержня – относительной продольной 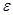и относительной поперечной :

, .

Экспериментально установлено, что при простом растяжении или сжатии между относительными поперечной и продольной деформациями существует зависимость:

,

где - коэффициент Пуассона, постоянный для данного материала.

Для подавляющего большинства конструкционных материалов с до­статочной для практики точностью можно считать, что в известных пределах нагружения между продольной деформацией и соответствующим (действующим в ее направлении) нормальным напряжением существует прямо пропорциональная (линейная) зависимость.Это положение носит название закона Гука и записывается в виде

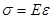. (2.2.3.)

Коэффициент пропорциональности Е называют модулем продольной упругости (другие названия: модуль нормальной упругости; модуль упругости; модуль упругости 1-го рода; мо­дуль Юнга). Очевидно, Е имеет ту же размерность, что и на­пряжение, т. е. выражается в Па или МПа. Модуль продольной упругости - физическая постоянная данного материала, характеризующая его жесткость. Чем жестче материал, тем меньше он деформируется при данном напряжении.

Для участка стержня длиной , на котором постоянны продольная сила и площадь поперечного сечения, закон Гука можно записать с учётом формул (2.2.2.) и (2.2.3.) в виде

.

Произведение EA называют жёсткостью сечения.

Для ступенчатого стержня (см., например, рис. 2.2.5.) абсолютное удлинение вычисляются для каждого 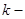го участка, а полное удлинение стержня определяют как их алгебраическую сумму:

.

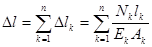Если продольная сила (см., например, рис. 2.2.4.) или площадь поперечного сечения изменяется по длине некоторого участка стержня непрерывно, используют формулу

.

В результате растяжения (сжатия) бруса его поперечные сечения перемещаются в направлении оси. Перемещения являются следствием деформации, но эти понятия следует строго разграничивать.

Перемещение 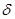одного сечения стержня относительно другого равно изменению длины участка стержня между этими сечениями. График, показывающий перемещения всех сечений стержня относительно неподвижного (или условно принятого за неподвижное), называют эпюрой перемещений.

Пример 4. Построить эпюры продольных сил, нормальных напряжений и осевых перемещений сечений стержня (рис. 2.2.7.), если , , , .

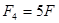Решение. Разбиваем стержень на участки, границами которых служат места приложения внешних сил и резкое, ступенчатое изменение площади сечения.

Строим эпюры продольных сил и нормальных напряжений, как это показано в примерах 1 и 3.

Для построения эпюры перемещений достаточно определить перемещения сечений, совпадающих с границами участков, так как между указанными сечениями эпюра линейна (почему?).

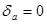Сечение неподвижно, т.е. . (построение эпюры перемещений следует всегда начинать от неподвижного или условно принятого неподвижным сечения). Вычисли перемещения остальных сечений:

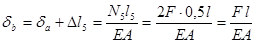(сечение перемещается от неподвижного сечения, т.е. вправо);

(сечение перемещается влево);

;

;

.

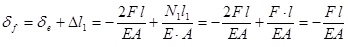На данном примере можно наглядно пояснить различие между понятиями деформации и перемещения. Так, на участке 11 продольная сила равна нулю, и, следовательно участок не деформируется, но все его сечения перемещаются относительно неподвижного.

Легко проверить правильность построения эпюры перемещений. Если на участке продольная сила положительная, значение 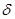увеличивается от сечения к сечению, если сила отрицательная – перемещение уменьшается. При отсутствии продольной силы перемещение всех сечений участка одинаково. Тангенс угла наклона эпюры 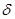пропорционален нормальному напряжению на участке.

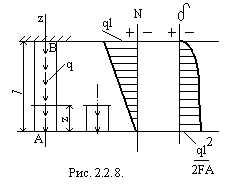Пример 5. Определить удлинение бруса постоянного поперечного сечения, нагруженного равномерно распределённой нагрузкой интенсивностью (рис. 2.2.8.).

Решение. Построение эпюры продольных сил разобрано в примере 3 (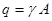). Продольная сила изменяется по линейному закону , поэтому удлинение определяем по формуле

.

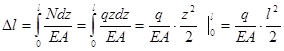Эпюра 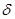ограничена параболой.

2.2.7. Конструктор, выбирая материал для проектируемой детали, а затем рассчитывая ее на прочность (жесткость, устойчивость), должен располагать данными о механических свойствах мате­риала, т. е. его прочности, пластичности и т. п., а также знать значения упругих постоянных - модуля Юнга Е и коэффициента Пуассона .

Основные механические характеристики, определяемые при испытаниях материалов:

1. Прочность - способность материала, не разрушаясь, вос­принимать внешние механические воздействия.

2. Пластичность — способность материала давать значи­тельные остаточные деформации, не разрушаясь.

3. Упругость — способность материала восстанавливать после снятия нагрузок свои первоначальные формы и размеры.

4. Твердость — способность материала сопротивляться про­никновению в него другого тела, практически не получающего остаточных деформаций.

Характер нагружения (статическое, динамическое, повторно-переменное) и условия работы деталей машин и инженерных сооружений весьма разнообразны. Располагая сведениями о свойствах материала при определенном виде деформации (например, растяжении) и характере нагружения (например, ста­тическом), судить о его свойствах при других условиях можно лишь весьма приближенно, что в ряде случаев недопустимо. Поэтому механические испытания материалов отличаются большим разнообразием.

По характеру нагружения различают испытания статические, динамические и испытания на усталость (при переменных напряжениях).

По виду деформации различают испытания на растяжение, сжатие, срез, кручение, изгиб. Реже проводят испытания при сложном нагружении, например на совместное действие изгиба и кручения.

Большинство испытаний проводится при нормальной (ком­натной) температуре, но для деталей паровых котлов, турбин, реактивных двигателей и т. п. необходимо знать их свойства при высоких температурах. В некоторых случаях возникает необходимость в испыта­ниях конструкционных материалов при низких температурах.

Механические испытания проводят на образцах, формы и размеры которых установлены ГОСТами или техническими условиями.

Механические испытания имеют большое значение не толь­ко для расчета на прочность, но и для контроля качества мате­риала или выпускаемых изделий. При этом испытаниям могут подвергаться как специально изготовленные образцы, так и са­ми изделия (детали или узлы).

Широко применяют механические испытания и в процессе создания новых конструкционных материалов, которые дол­жны обладать определенными механическими свойствами.

Помимо испытаний, при которых определяют механические характеристики, важное значение имеют различные технологи­ческие испытания (пробы), выявляющие соответствие свойств металла тому или иному технологическому процессу, например испытание листовой латуни на выдавливание с целью определения её пригодности для изготовления деталей холодной штамповкой.

Наиболее распространенным является испытание на растя­жение статической нагрузкой. Его достоинства — однородность напряженного состояния образца в области, достаточно уда­ленной от головок, сравнительная простота оборудования и методики эксперимента по сравнению с боль­шинством других испытаний. Однородность (т. е. тождествен­ность для всех точек тела) напряженного состояния позволяет легче обнаружить начало общей пластической деформации образца, что очень важно для определения соответствующих механических характеристик.

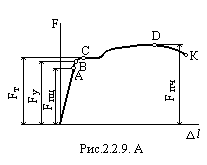Испытания проводят на разрывных или универсальных машинах с механическим или гидравлическим силообразованием. Большинство машин имеет устройство, автоматически вычерчивающее на бумажной ленте зависимость между нагрузкой, растягивающей образец, и его удлинением. Этот график называется диаграммой растяжения (рис. 2.2.9. А).

Ясно, что сила и удлинения, соответствующие указанным характерным точкам диаграммы, зависят не только от свойств материала, но и от абсолютных размеров образца. Для получения механических характеристик материала эту диаграмму перестраивают: все ординаты делят на начальную площадь поперечного сечения , а все абсциссы – на начальную расчётную длину . В результате получают условную диаграмму растяжения (рис. 2.2.9, Б),где

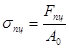- предел пропорциональности - наибольшее напря­жение, до достижения которого справедлив закон Гука;

- предел упругости - наибольшее напряжение, до достижения которого в образце не возникает остаточных деформаций;

- предел текучести (или физический предел текучести) - напряжение, при котором про­исходит рост пластических деформаций образца при практически постоянной нагрузке (в этой стадии деформации полированная поверхность образца становится матовой и на ней можно обнаружить сетку линий, наклонённых к оси образца под углом примерно 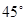- следы сдвигов частиц материала);

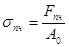- предел прочности - условное напряжение, соответствующее наибольшей нагрузке, выдерживаемой образцом до разрушения (отношение максимальной силы, которую способен выдержать образец, к начальной площади его поперечного сечения).

Диаграмма растяжений, показанная на рис. 2.2.9. Б, имеет ярко выраженную площадку текучести и характерна лишь для малоуглеродистой стали и некоторых сплавов цветных металлов. Диаграммы растяжения некоторых пластичных металлов и сплавов (среднеуглеродистые стали, меди, дюралюмина) не имеют площадки текучести. Для них вводится понятие условного предела текучести , представляющего собой напряжение, при котором относительное удлинение образца равно 0,2 %. Условный предел текучести определяют также для легированной стали и ковкого чугуна.

Хрупкие материалы (чугун, и т.д.)характерны тем, что их разрушение происходит при очень малых остаточных деформациях, поэтому при испытаниях на растяжение образцов чугуна определяют предел прочности . Условна диаграмма растяжения серого чугуна показана на рис. 2.2.10. Б.

На рис. 2.2.10. В. показана условная диаграмма сжатия малоуглеродистой ста­ли. При больших сжимающих нагрузках образец пластически деформируется (расплющивается), но не разрушается. Таким образом, для пластичных материалов по­нятия «предел прочности при сжатии» не существует. Условная диаграмма сжатия малоуглеродистой стали до предела текучести подобна диаграмме растяже­ния, но площадка текучести выявлена слабо. При пластической деформации образца его сечение увеличи­вается и нагрузка, требуемая для дальнейшего сжатия, возра­стает, что и объясняет характер диаграммы за пределом текучести. Значения пределов пропорциональности и текучести для пластичных материалов при растяжении и сжатии практически оди­наковы.

Для большинства пластичных материа­лов в результате испытаний на сжатие определяют условный предел текучести 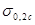. К материалам, для которых , относятся некоторые легированные стали, подвергнутые закалке. Такие материалы называют хрупкопластичными.

При разрушении образца из серо­го чугуна трещины появляющиеся на образце в начале разру­шения и направлены они под углом примерно 45° к его оси. На рис. 2.2.10. Г показана соответствующая диаграмма сжатия. При возникновении первых трещин нагрузка начинает падать и ис­пытание прекращается. Единственная характеристика, получаемая в результате этого испытания, - предел прочности при сжатии Чугун значительно лучше сопротивляется сжатию, чем растяжению. Предел прочности при сжатии в 3 - 4,5 раза выше, чем при растяжении .

2.2.8. Условие прочност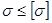и или 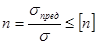должно соблюдаться для всех точек рассчитываемого элемента конструкции, поэтому под 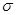следует понимать наибольшее расчётное напряжение. Здесь необходимо сделать оговорку: незначительное превы­шение наибольших расчетных напряжений над допускаемыми, конечно, не опасно, так как допускаемое напряжение составляет лишь некоторую часть от предельного. Обычно считают, что это превышение может составлять до 3% от допускаемого на­пряжения. Иными словами, в отдельных случаях считают воз­можным иметь коэффициент запаса несколько меньший, чем требуемый (заданный). Если расчетное напряжение значительно ниже допускаемого, это является свидетельством нерациональ­ности конструкции, перерасхода материала.

Условие прочности бруса при растяжении (сжатии) имеет вид

,

где 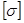- допускаемое напряжение ( 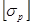при растяжении и 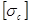при сжатии); А- площадь опасного поперечного сечения; N- продольная сила в указанном сечении.

Если материал имеет различные характеристики прочности при растяжении и сжатии, то условие прочности следует составлять для двух точек с наибольшим напряжение в зонах растяжения и сжатия.

Условие жёсткости записывают в виде

,

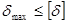где 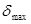-максимальное перемещение сечений; -допускаемое перемещение сечений.

Дата добавления: 2015-06-30