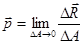Тема 2.1. Основные понятия и положения сопротивления материалов

РЯЗАНЬ

СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ

ЧАСТЬ 2.

По

РАБОЧАЯ ТЕТРАДЬ

ТЕХНИЧЕСКОЙ МЕХАНИКЕ

студента курса

группы

(Фамилия, имя, отчество)

СОДЕРЖАНИЕ

Пояснительная записка……………………………………………………………………………….3

Тема 2.1. Основные понятия и положения сопротивления материалов…………………………..4

Тема 2.2. Растяжение и сжатие……………………………………………………………………...13

Тема 2.3. Срез и смятие……………………………………………………………………………...25

Тема 2.4. Геометрические характеристики плоских сечений…………………………………...32

Тема 2.5. Кручение…………………………………………………………………………………..36

Тема 2.6. Изгиб………………………………………………………………………………………47

Тема 2.7. Расчёты на прочность при сложном напряжённом состоянии………………………..67

Тема 2.8. Расчёты на прочность при переменных напряжениях…………………………………80

Тема 2.9. Расчёты на прочность при динамических нагрузках………………………………….88

Тема 2.10. Устойчивость центрально сжатых стержней………………………………………….90

Вопросы для подготовки к зачёту по сопротивлению материалов………………………………94

Список литературы…………………………………………………………………………………95

Пояснительная записка.

Учебное пособие «Рабочая тетрадь по сопротивлению материалов» предназначено для студентов машиностроительных и транспортных специальностей техникумов очной и заочной формы обучения.

Пособие составлено в соответствии с Примерной программой учебной дисциплины «Техническая механика» для специальности 1705 «Техническое обслуживание и ремонт автомобильного транспорта».

В соответствии с программой сопротивление материалов представляет собой не отдельный учебный предмет, а один из разделов курса «Техническая механика». В результате изучения данного раздела студент должен:

иметь представление:

о роли и месте знаний по данному разделу при освоении дисциплины «Техническая механика» и в сфере профессиональной деятельности техника;

знать:

методику расчёта элементов конструкций на прочность, жёсткость и устойчивость при различных видах деформации;

уметь:

применять при анализе механического состояния тела терминологию технической механики;

выделять из системы тел рассматриваемое тело и силы, действующие на него;

определять характер нагружения и напряжённое состояние в точке элемента конструкций;

проводить несложные расчёты элементов конструкции на прочность и жёсткость;

использовать справочную документацию.

Настоящее пособие по каждой теме содержит:

номер и наименование темы;

план изучения темы;

теоретический материал;

вопросы для самопроверки;

задачи, предназначенные для решения на аудиторных занятиях и дома.

Нумерация пунктов, формул, рисунков и задач в каждой теме самостоятельная.

После каждого занятия учащиеся получают на дом задание по проработке теоретического материала и по решению задач. При выполнении домашнего задания следует придерживаться такой последовательности: сначала внимательно и вдумчиво прочитать теоретический материал, разобраться в основных понятиях, определениях законах, правилах и следствиях; затем ответить на вопросы для самопроверки. Ответы на вопросы рекомендуется кратко записать, а затем просмотреть прочитанный материал, чтобы убедится в правильности ответов. Приступая к решению задач, следует предварительно повторить вопросы ранее изученных тем, касающиеся содержания данной задачи. Перечень задач, выносимых на самостоятельное решение дома определяется непосредственно преподавателем дисциплины. Самостоятельное решение достаточно большого числа задач – непременное условие успешного овладения учебным материалом.

В пособии приведён перечень учебной литературы и вопросы для подготовки к зачёту по сопротивлению материала и экзамену.

Рабочая тетрадь не содержит описания лабораторных, практических и расчётно - графичесих работ. Наименования работ и указания по их проведению преподаватель выдаёт отдельно. Такие работы студенты должны выполнять в специально отведённых для этого тетрадях.

Изучение курса сопротивления материалов следует начать с повторения раздела «Статика».

2.1.1.Основные задачи сопротивления материалов.

2.1.2. Классификация внешних сил.

2.1.3. Допущения, принимаемые в сопротивлении материалов. Реальный объект и расчётная схема.

2.1.4. Внутренние силовые факторы. Метод сечений.

2.1.5. Механические напряжения. Напряжённое состояние в точке.

2.1.6. Коэффициент запаса прочности и условие прочности.

2.1.7. Перемещения и деформации.

2.1.8. Расчёты на жёсткость.

2.1.9. Три вида расчётов на прочность и жёсткость.

2.1.1. Сопротивление материалов представляет собой одно из направлений механики деформируемого твёрдого тела, которое под действием приложенных к нему сил изменяет свою форму и размеры – деформируется.

Деформации, исчезающие после снятия нагрузок, называются упругими; деформации, сохраняемые телом после удаления нагрузки, называют остаточными, или пластическими.

В сопротивление материалов изложены принципы и методы расчёта наиболее распространенных элементов различных конструкций на прочность, жёсткость и устойчивость.

Под прочностью понимаю способность конструкций или её отдельных элементов выдерживать заданные нагрузки без разрушения или появления в них пластических деформаций. Расчёт на прочность служит для установления минимально необходимых размеров элементов конструкций, исключающих возможность её разрушения или появления в ней пластических деформаций при действии заданных нагрузок. Неправильный расчет на прочность самой, на первый взгляд, незначительной детали может повлечь за собой очень тяжелые последствия, привести к разрушению всей конструкции.

Под жёсткостью понимают способность конструкций или её отдельных элементов сопротивляться образованию деформаций. При расчёте на жёсткость размеры элемента конструкции определяют из условия, что при действии на неё рабочих нагрузок происходящие при этом изменения формы и размеров элемента находятся в пределах, не нарушающих нормальную эксплуатацию конструкции. Если под воздействием внешних нагрузок какой-то её элемент существенно изменит свои первоначальные размеры, то может произойти нарушение работоспособности данной конструкции. Например, значительные прогибы валов зубчатой передачи приводят к неравномерному распределению нагрузки по длине зубьев, что связано с повышенным износом и даже опасностью поломки зубьев.

Под устойчивостью понимают способность конструкции сопротивляться усилиям, стремящимся вывести её из первоначальной формы упругого равновесия. Простей­ший пример такого явления представляет так назы­ваемый продольный изгиб сжатого стержня — при некотором значении сжимающей силы происходит выпучивание прямолинейного стержня, практически равносильное разрушению. Такое качественное изме­нение характера деформации конструкции при увели­чении нагрузки называется потерей устойчивости. Расчет конструкции, имеющий целью не допустить потери устойчивости, называется расчетом на устой­чивость.

При проведении расчетов необходимо сочетать надежность работы конструкции с её экономичностью, получать необходимые прочность, жесткость и устойчивость при наименьшем расходе материала.

Сопротивление материалов является эксперимен­тально-теоретической наукой, основные положения которой проверяются и дополняются экспериментальными исследованиями.. Опытная про­верка теоретических расчетов и формул необходима потому, что они основаны на ряде упрощающих предпосылок и допу­щений. Эти предпосылки и допущения связаны как со свойства­ми материалов, так и с характером деформаций элементов кон­струкций. В ряде случаев приходится специально изготовлять модель проектируемой конструкции (или отдельных ее элемен­тов) и подвергать ее испытаниям, чтобы получить данные о ха­рактере и величине деформаций, так как чисто теоретическим путем создание методов расчета оказывается вообще невоз­можным. Наконец, необходимо учесть, что все расчеты, выпол­няемые методом сопротивления материалов, базируются на знании физико-химических свойств конструкционных материа­лов. Эти свойства определяют путем лабораторных испытаний специально изготовленных образцов.

Сопротивление материалов тесно связано с материаловедением и теоретической механикой и базируется на основных законах и теоремах теоретической механики и, в первую очередь, широко использует уравнения равновесия различных систем сил, получен­ные в статике для абсолютно твердого тела. Однако, следует отметить и их принципиальное отличие: в теоре­тической механике для упрощения решения задач все тела прини­маются абсолютно твердыми; в сопротивлении материалов, как это и есть на самом деле,—деформируемыми, т. е. способными изменять первоначальную форму и размеры при действии на них внешних сил.

2.1.2. Каждый элемент конструкции работает совместно с другими элементами. Элемент можно рассматривать отдельно от дру­гих, если их действие на него заменить силами, которые по отношению к рассматриваемому элементу можно считать внешними. К внешним относят как силы, передаваемые дру­гими элементами, так и реакции связей (опор). Систему внешних сил, действующих на тело, называют нагрузкой.

Внешние силы подразделяют на объемные, распределен­ные по объему элемента (например, сила тяжести), и поверх­ностные, действующие на поверхность элемента. Поверхно­стные силы подразделяют на распределенные и сосредото­ченные. Силы могут быть распределены по поверхности эле­мента (например, давление газа в сосуде) и по его длине (например, вес балки условно можно считать равномерно распределенным по ее длине). Если площадь или длина, по которой распределены силы, мала по сравнению со всей пло­щадью поверхности или длиной элемента, то можно считать силы сосредоточенными в точке (например, давление колеса вагона на рельс), что существенно упрощает расчетную схе­му элемента.

По характеру изменения во времени нагрузки подразде­ляют на статические и динамические. Статическими называют нагрузки, абсолютное значе­ние, направление и место приложения которых постоянны или изменяются настолько медленно, что возникающими при этом ускорениями, а следовательно, и силами инерции можно пренебречь (например, сила затяжки болтов). Динамическими называют нагрузки, абсолютное значе­ние, направление или место приложения которых изменя­ются с большой скоростью так, что пренебречь возникающи­ми при этом силами инерции нельзя. Динамические нагруз­ки могут действовать кратковременно (например, ударные нагрузки) или повторно, изменяясь во времени по некоторому закону (например, нагрузки на зубья зубчатых колёс, шарики подшипников качения).

2.1.3. Наука о сопротивлении материалов, отказываясь от приня­того в теоретической механике допущения об абсолютной жесткости тел, все же не может при построении теории расче­тов на прочность и жесткость отразить все многообразие свойств реальных материалов. Поэтому в сопротивление мате­риалов приходится вводить ряд допущений относительно свойств материалов, позволяющих построить достаточно про­стую и удобную для инженерной практики теорию расчетов элементов конструкций. Конечно, эти допущения таковы, что полученные на их основе выводы достаточно точно совпадают с результатами соответствующих экспериментальных исследо­ваний.

Рассмотрим эти допущения.

1. Материал представляет собой сплошную среду, т. е. полностью заполняет объем тела. Это допущение позволяет использовать в сопротивлении материалов методы матема­тического анализа (дифференциальное и интегральное ис­числения).

2. Материал однороден, т. е. характеристики материала во всех точках изготовленной из него детали одинаковы.

3. Материал изотропен, т. е. обладает одинаковыми физико-механическими свойствами во всех направлениях. Материалы, имеющие различные свойства в разных направлениях, называют ани­зотропными (например, дерево). Металлы и сплавы, как правило, изотропны.

4. Материал идеально упругий, т. е. после снятия нагру­зок деформации полностью исчезают. Это допущение спра­ведливо, пока нагрузки не превышают определенного зна­чения. При больших нагрузках в элементах конструкций появляются пластические деформации.

5. Перемещения, возникающие под действием внешних сил в упругом теле, малы по сравнению с его размерами. Это допущение называется принципом начальных размеров. Допущение позволяет при составлении уравнений равновесия пренебречь изменениями формы и размеров конструк­ции.

6. Допущение (принцип) о независимости действия сил. Результат действия на тело системы сил не зависит от после­довательности их приложения и равен сумме результатов дей­ствия каждой силы в отдельности. Так, перемещение сечения балки (прогиб) при действии на нее сил 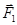и 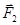(рис. 2.1.1.,В ) можно определить как сумму перемещений, вызванных раз­дельно приложенными силам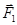и и 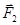(рис. 2.1.1., А и Б).

7. Гипотеза Бернулли. В сопротивлении материа­лов используют допущение (гипотезу) о том, что сечения бруса при его деформировании остаются плоскими и нормальными к оси бруса.

Расчет реального объекта в сопротивлении материалов начинают с выбора расчетной схемы. При замене реаль­ного объекта расчетной схемой устанавливают, что в данном расчете является существенным, а чем для упроще­ния расчета можно пренебречь. Упрощают по возможности форму объекта, устанавливают, к какому типу (брус, обо­лочка, массив) его можно отнести, схематизируют действую­щие на объект нагрузки, выясняя, к какому типу их следует отнести: статическим или динамическим, сосредоточенным или распределенным. Устанавливают тип опор по числу на­кладываемых на объект связей. При выборе расчётной схемы руководствуются основным правилом: максимально упрос­тить расчет, отбросив факторы, не влияю­щие заметно на конечный результат. Конеч­но, при выборе расчетной схемы необходи­мо иметь ясные представления о точности расчета, о погрешностях, возникающих при не учете тех или иных факторов. Например, при расчете на прочность троса, поднимающего груз, можно не учитывать форму поднимаемого груза, сопротивление воздуха, изменение давления и температуры воздуха с высотой, силу тяжести троса и многие другие факто­ры, учет которых усложняет расчет троса, но практически не влияет на конечный ре­зультат. Трос, свитый из большого числа тонких проволочек, в данном примере мож­но рассматривать как однородный стержень круглого по­перечного сечения, нагруженный растягивающей силой, со­средоточенной в месте крепления груза.

Все разнообразные элементы машин и сооружений при расчете на прочность и жесткость можно отнести к одному из трех типов:

· брус — тело, один из размеров которого (длина) значи­тельно больше двух других (рис. 2.1.2.,А);

· оболочка — тело, ограниченное двумя криволинейными поверхностями, расстояние между которыми (толщина) зна­чительно меньше двух других размеров (рис. 2.1.2.,Б ); част­ный случай оболочки — пластина — тело, ограниченное дву­мя плоскостями, расстояние между которыми (толщина) значительно меньше двух других размеров (рис. 2.1.2.,В);

· массив — тело, все три размера которого имеют один по­рядок (рис. 2.1.2.,Г).

2.1.4. Прочность твердого тела обусловлена силами сцепления между отдельными его частицами. При деформации тела, вы­званной действием приложенных к нему внешних сил, внутрен­ние силы изменяются. В дальнейшем под внутренними силами будем подразумевать не их абсолютные значения, а только те приращения, которые вызваны действующими на тело нагрузками. При возрастании внешних сил увеличиваются и внутрен­ние силы, но лишь до определенного предела, при превышении которого наступает разрушение. Это предельное значение вну­тренних сил зависит от физико-механических свойств материа­ла данного тела.

Для расчета на прочность необходимо иметь возможность определять внутренние силы по заданным внешним силам. Ос­нову для решения этой задачи дает метод сечений.

В дальнейшем наиболее часто метод сечений будет приме­няться для определения статических эквивалентов внутренних сил, возникающих в поперечных сечениях прямого бруса, по­этому специально остановимся на этом вопросе.

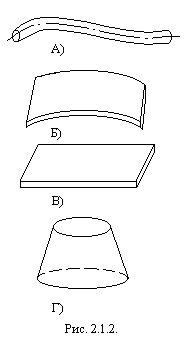
Рассмотрим прямой брус (рис. 2.1.3. А), находящийся в равновесии под действием произвольной системы внешних (активных и реак­тивных) сил. Рассечем его на две части (1 и 11)неко­торой произвольной плоскостью, перпендикулярной его про­дольной оси, и отбросим одну из частей (например, 1) и рассмотрим оставленную. Для обеспечения равновесия этой части надо приложить по прове­денному сечению те силы взаимодействия между частями 1 и11тела, которые были внутренними силами для целого тела (рис. 2.1.3. Б). Эти силы заменяют действие отброшенной части на оставлен­ную.

Принципиально совершенно безразлично, какую из частей тела (1 или 11) отбросить, так как из третьего закона Ньютона следует, что силы, действующие от части 11 на часть 1, равны по модулю и противоположны по направлению силам дей­ствия части 1 на 11. Практически удобнее оставлять ту часть, к которой приложено меньше внешних сил, так как уравнения равновесия для нее будут иметь более простой вид.

Внутренние силы по сечению распре­делены сплошь, но как именно они распределены, методами статики установить нельзя. Вместе с тем из тео­ретической механики известно, что любая система сил может быть приведена к ее главному вектору и главному моменту (2.1.3. В), ко­торые статически эквивалент­ны заданной системе сил. Далее известно, что главный вектор си­стемы может быть представлен ввиде трех составляющих по осям выбранной системы коор­динат. Аналогично, главный момент может быть также раз­ложен на составляющие по осям координат, т. е. заменен тремя моментами, каждый из которых стремится повернуть тело вокруг одной из коорди­натных осей (2.1.3. Г). Систему координат выби­раем следующим образом: начало координат О помещаем в центре тяжести рассматри­ваемого поперечного сечения, ось Oz направляем по внешней нормали к сечению, т. е. вдоль оси бруса, оси Ох и Оу располагаем в плоскости сечения, ось Оу — по оси симмет­рии поперечного сечения и ось Ох — ей перпендикулярно (в том случае, когда поперечное сечение бруса не имеет ни одной оси симметрии, оси Ох и Оу совпадают с так называемыми главными центральными осями сечения (это понятие разъяснено в теме 2.4.).

Составляющие главного вектора и главного момента вну­тренних сил, возникающих в поперечном сечении бруса, носят название внутренних силовых факторов в этом сечении.

На рис. 2.1.3. Г показаны шесть внутренних силовых факторов, возникающих в поперечном сечении бруса в общем случае его нагружения. Указанные шесть внутренних силовых факторов имеют сле­дующие наименования:

— продольная (или нормальная сила);

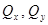- поперечные силы;

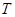— крутящий момент;

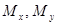— изгибающие моменты.

Каждый из них связан с определенным видом деформации бруса. Так, например, если не равна нулю только продольная сила 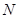, брус работает на растяжение или на сжатие. Если не равна нулю поперечная сила 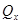(или 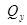, или обе одновремен­но), брус работает на срез (сдвиг). При наличии в поперечных сечениях бруса только крутяще­го момента 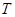имеет место деформация кручения. В случае ес­ли не равен нулю изгибающий момент 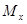или 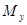, брус рабо­тает на чистый изгиб в плоскости yOx или xOz.

Таким образом, разложение главного вектора и главного момента внутренних сил на составляющие имеет не фор­мальный, а ясно выраженный физический смысл.

Для определения каждого из внутренних силовых факторов надо составить соответствующее уравнение равновесия для всех сил, действующих на оставленную часть бруса. Как известно, для пространственной системы произвольно рас­положенных сил таких уравнений может быть составлено шесть и в каждое из них войдет лишь один внутренний сило­вой фактор, который и будет определен из этого уравнения:

, , ,

, , .

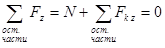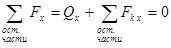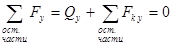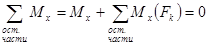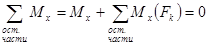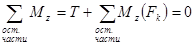2.1.5. Внутренние силы, как уже указывалось, распределены по се­чению тела (в частности, бруса) сплошь, при этом в общем слу­чае их значение и направление в отдельных точках сечения раз­личны. Для суждения об интенсивности внутренних сил в определенной точке данного сечения введено понятие механического напряжения (или просто напряжения).

Выделим в окрестности интересующей нас точки сечения малую площадку, площадью ; допустим, что на этой пло­щадке возникает внутренняя сила 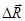(рис. 2.1.4. А). Отношение этой внутренней силы к площади выделенной площадки назы­вается средним напряжением 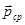в окрестности рассматривае­мой точки по проведенному сечению (на площадке ):

_.

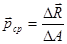Чем точнее нужно знать интенсивность внутренних сил в данной точке сечения, тем меньше должна быть выделенная площадка. В пределе при стремлении к нулю получим истинное на­пряжение в данной точке рассматриваемого сечения:

(2.1.1.)

Заметим, что при уменьшении площадки («стягивании» ее в точку) также стремится к нулю, но из физических соображений очевидно, что рассматриваемое отношение будет величиной конечной.

Напряжение в данной точке по рассматриваемому сечению есть величина векторная (вектор 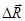делим на скаляр );на­правление этого вектора совпадает с предельным направлением вектора 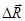, которое он имеет при уменьшении до нуля.

В Международной системе единиц (СИ) в качестве единицы напряжения принят паскаль (Па). Паскаль - это напряжение, при котором на площадке в 1м² возникает внутренняя сила, равная 1 Н, но эта единица очень мала, поэтому используется кратная ей единица — мегапаскаль, 1 МПа = 10⁶ Па.

Через данную точку тела можно провести бесчисленное множество сечений, различно ориентированных в пространстве, и, конечно, в общем случае возникающие на них напряжения будут различны. Поэтому нельзя говорить о напряжении в данной точке, не указывая площадки (сечения), на которой это напряжение возникает.

Совокупность напряжений, действующих в данной точке по всем сечениям, называют напряжённым состоянием в точке.

Разложим вектор напряжения 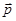на две составляющие: од­ну 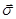(«сигма») — направленную по нормали к сечению, вторую 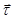(«тау»)— лежащую в плоскости сечения (рис. 2.1.4. Б). Составляющую напряжения 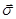, на­правленную по нормали к площадке ее действия, назовем нор­мальным напряжением, а составляющую 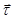, лежащую в плоскости сечения, — касательным напряжением. Между напряжениями 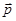, , 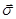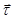существует следующая очевидная зависимость:

.

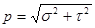Такое разложение полного напряжения имеет определенный физический смысл. Действительно, нормальное напряжение возникает тогда, когда частицы материала, соприкасающиеся по рассматриваемой площадке, под действием приложенных к телу нагрузок стремятся отдалиться друг от друга или сбли­зиться в направлении нормали к этой площадке, т. е. при рас­тяжении или сжатии. Касательные напряжения связаны со сдвигом частиц материала по плоскости рассматриваемого сечения.

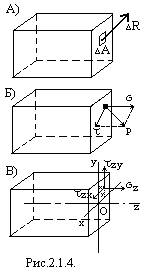
В ряде случаев оказывается удобным разложить вектор 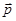не на две, а на три составляющие, направленные параллельно координатным осям. На рис. 2.1.4. В показано это разложение применительно к точке, взятой в поперечном сечении бруса.

Зависимость между полным напряжением и тремя его со­ставляющими выражается формулой

.

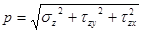Установим связь между напряжениями и внутренними си­ловыми факторами в поперечном сечении бруса. Умножая напряжения 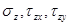на площадь 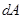площадки их действия, получаем элементарные внутренние силы (рис.2.1.4. В):

.

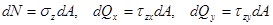Суммируя эти элементарные силы по всей площади сечения, получаем выражения составляющих главного вектора внутрен­них сил:

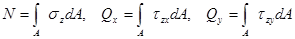. (2.1.2.)

Умножая каждую из элементарных сил на расстояние до со­ответствующей оси, получаем элементарные моменты внутрен­них сил:

.

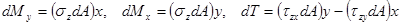Суммируя элементарные моменты по всей площади сече­ния, получаем выражения для составляющих главного момента внутренних сил:

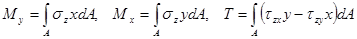. (2.1.3.)

Обращаем внимание, что выражения (2.1.2.), (2.1.3.) не служат для вычисления внутренних силовых факторов; значения по­следних определяют с помощью метода сечений, как указано в п.2.1.4. Эти выражения можно рассматривать как записанные с помощью математических символов определения, выражаю­щие физическую сущность внутренних силовых факторов. В дальнейшем эти выражения будут использованы при опре­делении напряжений по известным внутренним силовым факто­рам.

Итак, от внешних сил с помощью метода сечений к вну­тренним силовым факторам, от них на основе интегральных зависимостей и дополнительных гипотез к напряжениям — та­ков в общих чертах план решения основной задачи сопротивле­ния материалов об определении напряжений, возникающих в поперечных сечениях бруса при различных видах его нагружения.

Важнейшей задачей расчёта конструкций является обеспечение её прочности в условиях эксплуатации. Нарушением прочности деталей конструкции, как уже было сказано, принято считать возникновение хотя бы в одной точке остаточных деформаций или признаков разрушения.

Напряжения, возникновение которых в материале детали при работе повлечёт за собой нарушение её прочности называются предельными или опасными.

Путём механических испытаний (см. тему 2.2.) для каждого материала определяются напряжения, при достижении которых в материале появляются признаки нарушения прочности: при достижении предела текучести – заметные остаточные деформации, при достижении предела прочности – признаки непосредственного разрушения – появление излома. Так как оба признака говорят о нарушении прочности, то напряжения, при которых они появляются, должны считаться недопустимыми. Таким образом к предельным напряжениямматериалов должны быть отнесены предел текучести и предел прочности материала.

Выясним, в каком случае в качестве предельного напряжения должен быть взят предел текучести и когда — предел прочности.. Все материалы можно разделить на две категории: пластичные и хрупкие. Их принципиальное отличие, заключается в том, что пластичные материалы перед разрушением имеют значительные остаточные деформации, а хрупкие — разрушаются при ничтожно малых деформациях. Отсюда следует, что если деталь выполнена из пластичного материала, то остаточные деформации, являющиеся наравне с признаками разрушения, критерием непрочности де­тали, должны возникнуть значительно раньше, т. е. при меньших напряжениях, чем признаки непосредственного разрушения, так как предел текучести материала будь то условный или физиче­ский, всегда меньше предела прочности. Таким образом, для пла­стичных материалов предельным напряжением будет предел те­кучести. Если же деталь изготовлена из хрупкого материала, то опа­саться возникновения остаточных деформаций не приходится — они ничтожно малы, опасаются самого разрушения, а потому в ка­честве предельного напряжения хрупкого материала берут предел прочности.

Во время работы на элементы конструкций действуют внешние, нагрузки, в результате чего в них возникают напряжения, которые могут оказаться для материала элементов настолько значитель­ными, что элемент разрушится. Для того, чтобы этого не произошло, необходимо предугадать, какие напряжения могут возникнуть в де­тали в рабочих условиях и, в случае необходимости, усилить данную деталь. Для этого производятся расчеты на прочность.

Напряжения, возникающие в поперечных сечениях детали при действии на нее рабочих нагрузок и определяемые расчетным пу­тем, называются рабочими или расчетными напряжениями. При рас­смотрении различных видов деформаций бруса будут получены формулы, позволяющие вычислять расчетные напряжения в по­перечных сечениях нагруженного бруса.

Следует обратить внимание, что величина расчетных напря­жений не зависит от материала деталей, а зависит лишь от дей­ствующих на нее нагрузок и размеров поперечного сечения.

Каждое сооружение, а также любой его элемент под действием эксплуатационных (рабочих) нагрузок должен обладать достаточ­ной прочностью. В машиностроении чаще всего применяется так называемый расчет по опасной точке. По этому расчету предпола­гается, что вероятность разрушения максимальна в той точке, где напряжения максимальны. Считается, что прочность элемента будет нарушена в том случае, если хотя бы в одной его точке воз­никнут остаточные деформации или появятся признаки хрупкого разрушения. Отсюда вытекает физическое условие прочности: де­таль может считаться прочной, если максимальные расчетные на­пряжения -(напряжения в опасной точке), возникающие в ней, будут меньше предельных напряжений материала, из которого выполнена данная деталь.

Однако, если максимальные расчетные напряжения незначи­тельно меньше предельных, то гарантировать прочность детали рискованно, так как далеко не всегда бывают точно известны дей­ствующие нагрузки, сам расчет может носить приближенный ха­рактер, и, наконец, могут иметь место некоторые отклонения дей­ствительных механических характеристик материала по сравнению с принятыми в расчете. Для надежной работы деталь должна об­ладать определенным запасом прочности.

Число, показывающее во сколько раз максимальное расчетное напряжение элемента меньше предельного напряжения материала, из которого он выполнен, называется коэффициентом запаса проч­ности элемента и обозначается n:

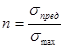. (2.1.4.)

Для деталей из пластичных материалов коэффициент запаса прочности определяется по пределу текучести, а из хрупких — по пределу прочности..

Деталь считается достаточно прочной, если ее коэффициент запаса прочности удовлетворяет конструктора. Чем больше коэф­фициент запаса прочности детали, тем она прочнее, но тем и тя­желее. Избыточный коэффициент запаса прочности детали приво­дит к утяжелению конструкции, делает ее неэкономичной. Из опыта проектирования и эксплуатации различных машин и конструкций устанавливаются минимально необходимые коэф­фициенты запаса прочности различных деталей, при которых будет гарантироваться их надежная работа. Различные ведомства, круп­ные заводы и проектные организации с учетом производственного опыта устанавливают свои нормы требуемых коэффициентов запа­сов прочности. Если по нормам, существующим для данного типа деталей, установлен требуемый (нормативный) коэффициент запаса прочности, обозначаемый 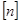, то прочность детали, будет обеспе­чена только в том случае, если ее расчетный коэффициент запаса прочности будет не ниже требуемого:

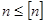. (2.1.5.)

Соблюдение требования (2.1.5.) носит название условия прочности. Если воспользоваться (2.1.4.), то условие прочности можно за­писать в виде

. (2.1.6.)

Обычно при назначении требуемого коэффициента запаса проч­ности в первую очередь учитывается следующее: 1)точность определения действующих нагрузок и точность методов расчета на прочность; 2) ответственность детали; 3) срок службы.

Чем точнее определены действующие на элемент нагрузки и чем точнее расчет, тем меньше можно назначить требуемый коэффи­циент запаса прочности. Для ответственных деталей, разрушение которых может привести к гибели людей или больших материальных ценностей, назначают высокий нормативный коэффициент запаса прочности. Для деталей одноразового использования, естественно, коэффициент запаса прочности меньше, чем для деталей, предназ­наченных для длительной эксплуатации.

Если для какой-либо детали по существующим нормам установ­лен требуемый коэффициент запаса прочности и выбран материал, а это значит, что известны его механические характеристики, то можно установить максимальное значение напряжений, при которых будет обеспечен требуемый запас прочности, и, следовательно, будет гарантироваться прочность самой детали.

Максимальные напряжения, которые можно допустить при ра­боте элемента и при которых будет обеспечен требуемый запас прочности, называются допускаемыми напряжениями и обознача­ются :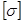

.

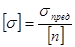Выясним, от чего же зависит величина допускаемых напряже­ний. Во-первых — от прочности материала (чем выше 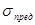, т. е., чем выше прочность материала, тем больше будут допускаемые на­пряжения, естественно, при одинаковом требуемом запасе прочно­сти), во-вторых — от всех тех факторов, которые влияют на вели­чину требуемого коэффициента запаса прочности.

Пользуясь понятием допускаемого напряжения, можно сформу­лировать условие прочности: рассчитываемый элемент считается прочным, если возникающее в его опасной точке максимальное напряжение не превышает допускаемого:

. (2.1.7.)

2.1.7. Как уже отмечалось выше, под действием нагрузки ре­альные твердые тела меняют свою форму и размеры. Следо­вательно, его точки, а также мысленно проведенные линии и сечения перемещаются в плоскости или пространстве.

Рассмотрим реальное тело (рис. 2.1.5.). Отметим в нем до нагружения точку А. После нагружения эта точка переме­стится в новое положение А' '. Вектор 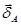, имеющий начало в точке А недеформированного тела, а конец в той же точке (А') деформированного тела, называют вектором линейного перемещения или просто перемещением точки А. Его состав­ляющие, параллельные осям координат х, у и z, носят наз­вание перемещений по осям и соответственно обозначаются через .

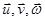Кроме линейного перемещения введем понятие углового перемещения. Если рассмотреть отрезок АВ прямой между двумя бесконечно близкими точками до нагружения (рис.2.1.6.), то после нагружения этот отрезок займет новое положение А'В'. Конечно, в общем случае при нагружении точки отрез­ка АВ могут получить различные перемещения и рассматри­ваемый отрезок может искривиться. Однако, приняв его бе­сконечно малым, можно утверждать, что после нагружения он сохранил свою прямолинейность. Угол 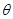, на который рас­сматриваемый отрезок повернулся в пространстве, принято называть угловым перемещением

Для характеристики интенсив­ности изменения размеров и формы тела введем понятие деформации. Длина отрезка АВ (см. рис. 2.1.6.) после нагружения изменится на 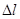. Отношение приращения длины отрезка АВ к его начальной длине называют средней линейной деформацией в точке А по направлению АВ:

.

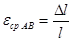В пределе при стремлении к нулю получим линейную деформацию в точке в рассматриваемом направлении:

.

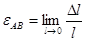Если через точку А провести отрезок другого направле­ния, то деформация будет другой. Обычно в качестве основ­ных принимают направления, параллельные осям выбранной прямоугольной системы коорди­нат. Тогда в обозначение 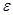вво­дят соответствующие индексы, т. е. .

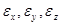Слово «деформация» имеет двоякий смысл. В разговорном языке под деформацией понима­ют вообще всякое изменение фор­мы без количественной оценки. В сопротивлении материалов де­формация имеет данное выше строгое определение и выступает как количественная мера измене­ния геометрических размеров в окрестности рассматривае­мой точки. Деформация — безразмерная величина.

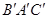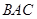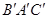Прямой угол, образованный двумя произвольными бесконечно малыми отрезками А В и АС (рис. 2.1.7.), после нагружения тела изменится и примет зна­чение . Разность углов и называют уг­ловой деформацией в точке А в плоскости ВАС и обозначают греческой буквой 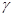(гамма) с индексом ВАС, т.е. 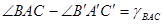. В той же точке А угловые деформации в различных плоскостях различны. Обычно угловые деформации определяют в трёх взаимно перпендикулярных координатных плоскостях и обозначают .

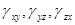2.1.8. Зачастую для нормальной работы элемента машины или какой-либо конструкции бывает недостаточно соблюдения лишь условия прочности. Помимо прочности к элементу может быть предъявлено требование необходимой жесткости. Напомним, что под жесткостью детали понимается ее способность воспринимать заданные внешние нагрузки, не деформируясь выше установленных норм.

Расчёт на жёсткость предусматривает определение максимальных перемещений, соответствующих данному виду деформаций и сопоставление их с допускаемыми перемещениями, величина которых устанавливается в зависимости от условий работы рассчитываемого элемента. Условие жёсткости можно сформулировать так: жёсткость элемента конструкции обеспечена, если максимальное перемещение сечения, соответствующее данному виду деформации, не превышает допускаемого перемещения:

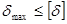. (2.1.8.)

2.1.9. В зависимости от цели задачи, от её исходных данных существует три вида расчётов на прочность и жёсткость: проверочный расчёт, проектный расчёт и определение допускаемой нагрузки.

1) Цель проверочного расчёта заключается в проверке прочности и жёсткости рассчитываемого узла, т.е. в проверке соблюдения условий прочности и жёсткости (формулы 2.1.7. и 2.1.8.). На этапе проведения проверочного расчёта должны быть заданы нагрузки, действующие на рассчитываемую конструкцию. Известны все её размеры и материалы, из которых она выполнена или должна быть выполнена. В результате расчёта могут быть выявлены слабые места конструкции, прочность или жёсткость которых оказалась недостаточной. В таком случае может быть предложена доработка конструкции или её отдельного элемента в части их упрочнения.

2. Задача проектного расчёта заключается в определении рациональной формы и размеров проектируемой конструкции при обязательном соблюдении условия прочности, а часто и условия жёсткости. На стадии проектного расчёта задаются рабочие нагрузки, оговариваются условия работы, срок службы, задаётся и назначается самим конструктором материал, определению подлежат размеры проектируемой детали. Размеры определяются таким образом, чтобы для опасной (наиболее нагруженной) точки соблюдалось условие прочности; в таком случае для всех остальных точек, а значит и для всей детали в целом. Условие прочности будет тем более удовлетворено. Уже отмечалось, что нередко при проектировании деталей и узлов предъявляется кроме требования прочности ещё требование достаточной жёсткости. Может случится, что в результате расчёта будут найдены два значения искомого размера (один из условия прочности, другой- из условия жёсткости), тогда в качестве окончательного следует принять тот, который удовлетворяет обоим условиям, т.е. наибольший.

3. Определение допускаемой нагрузки. Если размеры элемента конструкции и допускаемое напряжение материала известны, то определить из условия прочности допускаемое значение нагрузки не представляет особого труда. Для опасной точки бруса записывается условие прочности (или жёсткости), а затем определяется допускаемое значение внутреннего силового фактора, по которому вычисляется допускаемая внешняя нагрузка.

Дата добавления: 2015-06-30