Тема 2.4. Геометрические характеристики плоских сечений

Для заметок

2.4.1. Статические моменты плоских сечений.

2.4.2. Моменты инерции плоских сечений.

2.4.3.Главные оси и главные моменты инерции сечений.

2.4.4. Главные моменты простейших сечений.

2.4.5. Главные момент инерции сложных сечений, имеющих ось симметрии.

2.4.1. Напряжения и деформации в брусе, как показано в предыдущих темах, зависят от внутренних силовых факторов (сил и моментов) и геометрических характеристик поперечного сечения. При расчётах на прочность при растяжении и сжатии такой характеристикой является площадь поперечного сечения. Форма сечения при этом значения не имеет. Независимость напряжения от формы сечения можно объяснить тем, что напряжения при растяжении (сжатии) распределяются по сечению равномерно. При кручении и изгибе на­пряжения неравномерно распределены по сечению, поэтому они зависят не только от размеров сечения, но и от его фор­мы. Геометрическими характеристиками сечения, входя­щими в расчетные формулы при кручении бруса, являются полярный момент инерции 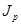и полярный момент сопро­тивления 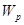(тема 2.5.). При расчетах бруса на прочность при изгибе необходимо знать такие геометрические характе­ристики сечения, как моменты инерции и моменты сопро­тивления сечения относительно определенных осей, проходя­щих через его центр тяжести (тема 2.6.). Координаты центра тяжести сечения определяют через статические моменты сечения и его площадь.

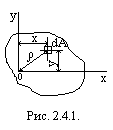Статическим моментом. плоского сечения (рис. 2.4.1.) относительно некоторой оси называют взятую по всей его площади А сумму про­изведений площадей элементарных площадок dA на их расстояние до этой оси:

, .

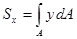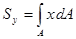Единицей статического момента является (в практике расчетов используют ).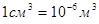

При известных координатах 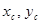центра тяжести се­чения статический момент равен произведению пло­щади сечения на расстояние от центра тяжести до этой оси

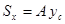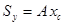, . (2.4.1.)

Из формулы (2.4.1.) вытекает весьма важное для дальнейшего следствие: статический момент сечения относительно любой центральной оси (проходящей через центр тяжести) равен нулю. Согласно формуле (2.4.1.) статический момент может быть как положительным, так и отрицательным.

При известных статических моментах сечения относи­тельно осей Ox, Oy координаты центра тяжести сечения в сис­теме координат Oxy определяют по формулам

, .

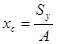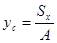Если сечение можно разбить на n простых фигур, пло­щадь и положение центра тяжести которых известны, стати­ческие моменты сечения можно определить как сумму ста­тических моментов его составных частей:

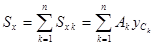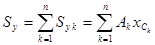, . (2.4.2.)

С учетом (2.4.2.) координаты центра тяжести составного сечения определяют по формулам

.

Для сечений, составленных из профилей стандартного проката (швеллеры, уголки, двутавры), площадь каждого профиля и остальные необходимые для расчётов размеры принимают по таблицам ГОСТов на прокатную сталь.

2.4.2. Моментом инерции сечения (см. рис. 2.4.1.) относительно некото­рой оси (осевым моментом инерции) называют взятую по всей площади сечения А сумму произведений площадей элементарных площадок dA на квадраты их расстояний до этой оси

, .

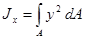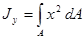Полярным моментом инерции сечения (см. рис. 2.4.1.) относи­тельно некоторой точки (полюса) называют взятую по всей площа­ди сечения А сумму произведений площадей элементарных площа­док dA на квадраты их расстояний до этой точки

.

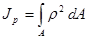Центробежным моментом инерции сечения (см. рис. 2.4.1) отно­сительно некоторых двух взаимно перпендикулярных осей называ­ют взятую по всей площади сечения А сумму произведений площа­дей элементарных площадок dA на их расстояния до этих осей

.

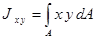Единицей моментов инерции является 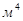. Осевые и по­лярный моменты инерции всегда положительны, центро­бежный момент может быть как положительным, так и от­рицательным, а также равным нулю.

Между осевыми и полярным моментами инерции се­чения имеется связь:

.

Сумма моментов инерции относительно двух взаимно перпенди­кулярных осей равна полярному моменту инерции относительно точки пересечения этих осей.

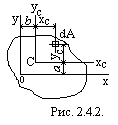В практических расчетах часто используют зависимость между моментами инерции относительно параллельных осей, одна из которых центральная. Допустим, известны положение цент­ра тяжести С сечения (рис. 2.4.2.) и мо­менты инерции 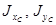относитель­но центральных осей 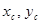. Такие моменты инерции называют цент­ральными. Установим зависимость между центральными моментами и моментами инерции относительно осей x и y,параллельных центральным при известных расстояниях а и b между осями:

,

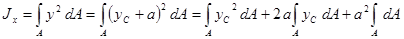где 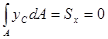(см. п. 2.4.1.), а значит

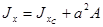. (2.4.3.)

Аналогично получим выражение

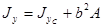. (2.4.4.)

Согласно формулам (2.4.3.) и (2.4.4.), центральный момент инерции имеет минимальное значение из моментов инерции относи­тельно параллельных осей, проведенных в сечении.

2.4.3. Как известно, через точку можно провести бесчисленное множество пар взаимно перпендикулярных осей. Моменты инерции относительно различных осей имеют различные значения.

Так как сумма осевых моментов инерции сечения относи­тельно двух взаимно перпендикулярных осей равна полярному моменту и, следовательно, есть величина постоянная, то, поворачивая систему координат, можно найти такое по­ложение осей, при котором относительно одной из осей момент инерции будет максимален, а относительно другой — минимален. Центробежный момент инерции относительно таких осей равен нулю.

Оси, относительно которых моменты инерции сечения имеют экс­тремальные значения, а центробежный момент инерции равен нулю, называют главными осями инерции. Моменты инерции относи­тельно главных осей называют главными моментами инерции.

Через любую точку сечения можно провести главные оси инерции, и, следовательно, главных моментов инерции бес­численное множество. В практических расчетах используют главные моменты инерции относительно осей, проходящих через центр тяжести сечения. Такие моменты называют главными центральными моментами инерции, а оси — главными центральными осями. Так как в расчетах используют только эти моменты, слово «центральные» опускают и моменты называют просто главными моментами инерции.

Как правило, поперечные сечения деталей машин и эле­ментов конструкций имеют хотя бы одну ось симметрии. Можно доказать, что ось симметрии сечения и перпендикулярная ей центральная ось являются главными центральными осями.

Если сечение имеет больше двух осей симметрии, например круг, квадрат, равносторонний треугольник, то для него все центральные оси являются главными, а главные центральные моменты инерции имеют одно значение.

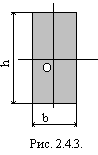
2.4.4. Пример 1. Определить моменты инерции прямоугольника с основанием b и высотой h относительно осей x и y (рис. 2.4.3.), проходящих через тяжести О прямоугольника параллельно его сторонам.

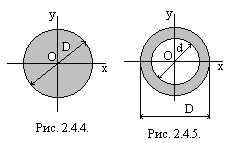
Пример 2. Определить полярные моменты инерции круга (рис. 2.4.4.) и кольца (2.4.5.) относительно их центров.

2.4.5. Главные центральные моменты инерции простейших сече­ний вычисляют по готовым формулам, наиболее распростра­ненные из которых приведены в предыдущем пункте. Раз­меры и геометрические характеристики профилей стандартного проката приведены в таблицах ГОСТа.

Для вычисления главных моментов инерции сложных (со­ставных) сечений их разбивают на простейшие части, моменты инерции которых определяют по готовым формулам или та­блицам. Дальнейший расчет ведут в следующем порядке (по-прежнему ограничиваемся сечениями, имеющими не менее одной оси симметрии).

1. Определяют положение центра тяжести сечения, а следо­вательно, и главных центральных осей.

2. Вычисляют (или берут из таблиц) значения моментов инерции отдельных частей сечения относительно собственных центральных осей, параллельных главным центральным осям всего сечения.

3. Вычисляют моменты инерции частей, составляющих сече­ние, относительно его главных центральных осей. При этом ис­пользуют зависимость между моментами инерции относитель­но параллельных осей (2.4.3.) и (2.4.4.).

4. Определяют главные центральные моменты инерции все­го сечения путем суммирования для каждой из главных осей величин, вычисленных в п. 3.

Таким образом, при вычислении моментов инерции со­ставных сечений руководствуются следующим правилом: момент инерции сечения относительно данной оси равен сумме моментов инерции составляющих это сечение частей относитель­но той же оси. Это правило вытекает из известного свойства определенно­го интеграла: интеграл суммы нескольких слагаемых равен сумме интегралов этих слагаемых.

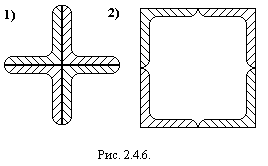
Пример 3. Сравнить главные моменты инерции сечений 1 и 2, составленных из четырёх равнополочных уголков № 10 (1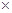00 100 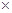10) (рис. 2.4.6.).

Дата добавления: 2015-06-30