Тема 2.5. Кручение. 1 страница

Для заметок

2.5.1. Чистый сдвиг.

Внутренние силовые факторы при кручении.

Напряжения при кручении бруса круглого поперечного сечения.

Расчёты на прочность при кручении

Перемещения при кручении бруса круглого поперечного сечения.

Расчёты на жёсткость при кручении.

.

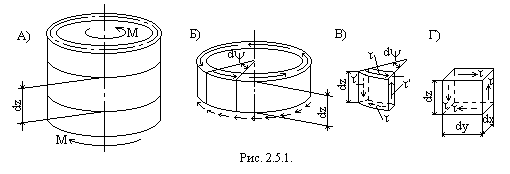2.5.1. Рассмотрим кручение тонкостенной цилиндрической трубы, нагруженной на торцах вращающими моментами М (рис. 2.5.1. А). В поперечных сечениях трубы (бруса) возникают только крутящие моменты численно равные внешним моментам М. При кручении бруса в его поперечных сече­ниях возникают силы взаимодействия частиц, сопротивляющиеся их взаимному смещению в плоскости сечения. Сумма моментов этих внутренних сил, лежащих в сечении, как показано в 2.1.5., представляет собой крутящий момент. Мерой интенсивности внутренних сил, лежащих в сечении, является касательное напряжение .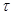

Используя метод сечений, вырежем из трубы двумя попе­речными сечениями бесконечно малый участок длиной 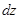(рис. 2.5.1. Б) и из него двумя радиальными сечениями с углом; между ними 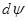— бесконечно малый элемент (рис. 2.5.1. В). Рассмотрим условия равновесия элемента. На гранях эле­мента, совпадающих с поперечными сечениями трубы, воз­никают касательные напряжения 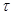. На гранях, совпадаю­щих с продольными сечениями, должны возникать каса­тельные напряжения 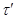(иначе не будет обеспечено равнове­сие элемента). Направление касательных напряжений 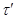должно быть таким, чтобы момент внутренних сил, дейст­вующих на этих гранях, уравновешивал момент внутренних сил, действующих на гранях, совпадающих с поперечными сечениями. На остальных двух гранях, совпадающих с на­ружной и внутренней поверхностями трубы, напряжений нет. Из условий равновесия системы сил, действующих на элемент:

.

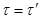По взаимно перпендикулярным граням действуют равные по абсолютному значению касательные напряжения, дающие пары сил противоположного направления. Это за­кон парности касательных напряжений (см. п. 2.2.5.).

Ввиду бесконечной малости элемента на рис. 2.5.1.В можно, пренебре­гая кривизной, рассматривать его как параллелепипед со сторонами dx, dy, dz (рис. 2.5.1. Г).

Напряжённое состояние, при котором можно выделить элемент таким образом, чтобы на четырёх его гранях были только равные между собой касательные напряжения, а две грани были от напряжений свободны, называется чистым сдвигом (рис. 2.5.1. Г).

Рассмотрим деформацию элемента при чистом сдвиге. Закрепим условно одну грань элемента, тогда под действием сдвигающей силы грань, параллельная закрепленной, сдви­нется на некоторую величину 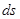. Прямые углы между гра­нями изменятся на угол сдвига 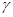(рис. 2.5.2.). Угол сдвига ха­рактеризует относительную угловую деформацию.

Экспериментально установлено, что в пределах упругого деформирования тела между углом сдвига и касательным напряжением существует линейная зависимость, выражае­мая законом Гука при сдвиге

.

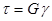Здесь G — модуль сдвига (модуль упругости второго рода), имеющий ту же размерность, что и напряжение 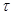, и связан­ный с модулем упругости 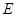и коэффициентом Пуассона 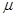зависимостью

.

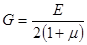Для стали принимают 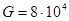МПа.

2.5.2. Кручением называют вид деформации бруса, при котором в его поперечных сечениях возникает один внутренний силовой фак­тор — крутящий момент .

Кручение бруса вызывают скручивающие (вращающие) моменты М, действующие в плоскостях, перпендикулярных оси бруса (рис. 2.5.3.).Брус, нагруженный вращающими мо­ментами, обычно называют валом. Во всех машинах и механизмах имеются валы с укреп­ленными на них различными деталями: зубчатыми колеса­ми, шкивами ременных передач, звездочками цепных пере­дач и т. д., передающими вращающие моменты.

При равномерном вращении вала сумма вращающих мо­ментов, действующих на вал, равна нулю.

При известных передаваемой мощности Р (Вт) и угловой скорости вала 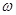(рад/с) вращающий момент М (Н • м) можно определить по формуле

.

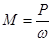Если известна частота вращения вала 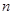, , 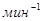то его уг­ловая скорость

.

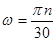В сопротивлении материалов реальный объект заменяют расчетной схемой, отбрасывая факторы, которые, не влияя заметно на результат, усложняют расчет. Составляя расчетную схему вала, допускают, что вращающие моменты не распреде­лены по ширине зубчатых колес, шкивов и других деталей, а сосре­доточены в их среднем сечении.

Участки вала между сечения­ми, в которых приложены внеш­ние моменты, скручиваются. Кру­тящий момент в любом сечении вала определяют методом сечений (см. рис. 2.5.3.). Рассекая мысленно вал плоскостью, от­брасывают одну (любую) часть вала, заменяют действие отброшенной части на оставленную моментом и определя­ют его значение из уравнения равновесия.

Крутящий моментв сечении вала численно равен алгебраической сумме внешних (вращающих, скручивающих) моментов, расположенных по одну сторону от сечения.

Если на вал действуют несколько вращающих момен­тов, то для определения опасного сечения или участка вала строят эпюры крутящих моментов аналогично эпюрам про­дольных сил.

В отличие от продольной силы, знак которой имеет опре­деленный физический смысл (растяжение или сжатие), знак крутящего момента физического смысла не имеет, поэтому на эпюрах 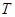его не указывают.

Условно крутящий момент считают положительным (при построении эпюр 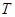), если, глядя на сечение со стороны внешней нормали к сечению, мы ви­дим крутящий момент, направленный против часовой стрелки. Так как по условию равновесия крутящий момент уравнове­шивает внешние моменты, приложенные к оставленной час­ти вала, то его знак противоположен знаку внешних момен­тов. При определении крутящего момента внешние момен­ты, действующие по часовой стрелке (если смотреть на сечение со стороны внешней нормали к сечению), считают положительными.

Характер деформирования при кручении существенно зависит от формы поперечного сечения бруса. Методами сопротивления материалов задача о напряжениях и перемещениях при кручении может быть решена только для бруса круглого сплошного или кольцевого поперечного сечения.

Методику построения эпюр крутящих моментов. рассмотрим на конкретных примерах.

Пример 1. Построить эпюры крутящих моментов для трансмиссионных валов на рис. А) и Б) и указать, какая из приведённых схем выгоднее. 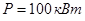- мощность, поступающая на ведущий шкив; 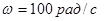- угловая скорость вала.

Дата добавления: 2015-06-30