Тема 2.6. Изгиб. 1 страница

Для заметок.

2.6.1. Основные понятия и определения. Виды изгиба.

2.6.2.Внутренние силовые факторы при изгибе.

2.6.3. Дифференциальные зависимости между изгибающим моментом, поперечной силой и интенсивностью распределённой нагрузки. Эпюры поперечных сил и изгибающих моментов

2.6.4. Нормальные напряжения при изгибе.

2.6.5. Расчёты на прочность при изгибе. Рациональные формы поперечных сечений брусьев.

2.6.6. Перемещения при изгибе. Метод Мора.

2.6.7. Расчёты на жёсткость при изгибе.

2.6.8. Касательные напряжения при прямом поперечном изгибе

2.6.1. Изгибом называют вид деформации бруса, при котором в его по­перечных сечениях возникают изгибающие моменты.

Различают несколько разновидностей изгиба. Если в по­перечных сечениях бруса возникают только изгибающие мо­менты, изгиб называют чистым. Если кроме изгибающих моментов в поперечных сечениях возникают поперечные си­лы, изгиб называют поперечным.

С геометрической точки зрения изгиб характеризуется тем, что ось бруса, прямолинейная до деформации, при изгибе становится криволинейной линией. Для криволинейного бруса изгиб связан с изменением кривизны его оси.

Внешние силы могут лежать в одной или нескольких плоскостях, проходящих через ось бруса. Такие плоскости называют силовыми. Плоскость, проходящая через ось бру­са и одну из главных осей инерции сечения, называют глав­ной.

Если все внешние силы лежат в одной силовой плоскос­ти, совпадающей с главной (рис. 2.6.1.), прямолинейная до из­гиба ось бруса искривляется, оставаясь плоской кривой, ле­жащей в той же плоскости, что и внешние силы. Такой из­гиб называют прямым. Если силовая плоскость не совпадает с главной плоскостью бруса (рис. 2.6.2.), его ось после изгиба будет расположена в плоскости, не совпадающей с главной. Такой изгиб называют косым (брус изгибается «косо» в том смысле, что направление нагрузок и прогибов не совпадают).

Брус, испытывающий изгиб, воспринимает внешние си­лы от других элементов конструкции и передаёт их на опоры. В опорах возникают реакции связей. По числу связей опоры подразделяют на три типа.

Шарнирно-подвижная опора накладывает на опорное сечение балки одну связь. Такая опора позволяет опор­ному сечению поворачиваться вокруг оси шарнира и пере­мещаться в направлении оси балки. Реакция опоры направлена перпендикулярно опорной плоскости — обычно оси балки.

Шарнирно-неподвижная опора накладывает на опорное сечение две связи, исключая его линейное перемещение и позволяя вращаться вокруг оси шарнира. Возникающая в опоре реакция лежит в той же плоскости, что и внешние си­лы. Для удобства расчета реакцию опоры раскладывают на две составляющие, направленные перпендикулярно и вдоль оси балки.

Жесткая заделка накладывает на опорное сечение три связи, исключающие все его перемещения в плоскости действия внешних сил (см. раздел «Теоретическая механика», п. 1.1.4.).

.Как правило, действующие на балку нагрузки можно от­вести к одному из трех видов: сосредоточенные силы F, со­средоточенные моменты М, распределенные нагрузки интенсивностью q (рис. 2.6.3.).

Достаточно очевидно, что при изгибе брус деформируется таким образом, что часть его волокон испытывает растяжение, а часть – сжатие. Волокна, расположенные в выпуклой части изогнутого бруса, растягиваются, а в вогнутой – сжимаются. Границей между областями растяжения и сжатия является слой волокон, который лишь искривляется, не испытывая при этом ни растяжения, ни сжатия. Это так называемый нейтральный слой. Линия пересечения нейтрального слоя с плоскостью поперечного сечения бруса называется нейтральной осью или нулевой линией.

2.6.2. При пря­мом поперечном изгибе (рис. 2.6.1.)в поперечных сечениях бруса (балки) возникают два внутренних силовых фактора: поперечная сила 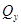и изгибающий момент 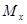. Зависимости между этими внутренними силовыми факторами инапряжениями в попереч­ном сечении бруса таковы:

; .

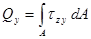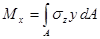Следовательно, в поперечных сечениях бруса в рассматри­ваемом случае изгиба возникают как касательные, так и нор­мальные напряжения.

Приведенные зависимости позволяют дать следующие определения поперечной силы и изгибающего момента:

Поперечной силой 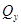называется равнодействующая внутрен­них касательных сил, возникающих в поперечном сечении бру­са.

Изгибающим моментом 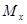называется результирующий мо­мент внутренних нормальных сил, возникающих в поперечном се­чении бруса, взятый относительно нейтральной оси этого сечения.

Конечно, приведенные зависимости между 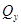и и 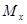напря­жениями не могут быть использованы для вычисления попе­речных сил и изгибающих моментов. Их определяют с по­мощью метода сечений через действующие на брус внешние силы.

Так же как при изучении растяжения (сжатия) и кручения, для наиболее наглядного представления о характере изменения внутренних силовых факторов 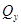и 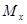по длине бруса и для нахождения его предположительно опасных сечений строят со­ответствующие графики — эпюры поперечных сил и изгибающих моментов. При этом брус (балку) изображают одной линией, к которой прило­жены заданные нагрузки. Эта линия представляет собой про­дольную ось бруса.

При прямом по­перечном изгибе, приходим к следующим правилам для вычис­ления поперечных сил и изгибающих моментов.

Поперечная сила 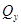в произвольном поперечном сечении бруса численно равна алгебраической сумме внешних сил, приложенных к его отсеченной части.

Изгибающий момент 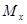в произвольном поперечном сечении бруса численно равен алгебраической сумме моментов всех внеш­них сил, приложенных к отсеченной части, относительно той точ­ки продольной оси бруса, через которую проходит рассматривае­мое сечение.

Для определенности при построении эпюр поперечных сил и изгибающих моментов установим для них правила знаков.

Поперечные силы счи­таются положительными, если онистремятся повернуть элемент по часовой стрелке (рис. 2.6.4).

Знак изгибающего момента связан с характером деформа­ции бруса: изгибающий момент считается положительным, если элемент бруса изгибается выпуклостью вниз (рис. 2.6.5.), т. е. таким образом, что его сжатые волокна находятся в верхней части.

Практически при построении эпюр удобнее устанавливать знак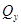и и 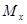по внешним силам; при этом результат должен быть одинаков с получаемым при определении знаков непос­редственно по внутренним силам.

Совпадение результатов получится при применении следую­щих правил.

Внешняя сила, стремящаяся повернуть отсеченную часть бал­ки по часовой стрелке вокруг той точки оси, которая соответ­ствует проведенному сечению, вызывает положительную попереч­ную силу.

Для определения знака изгибающего момента следует во­образить отсеченную часть балки защемленной в проведенном сечении.

Внешняя сила (момент), изгибающая эту часть выпуклостью вниз, т. е. таким образом, что сжатые волокна находятся сверху, дает положительный изгибающий момент.

Подчеркнем, что, рассматривая отсеченную часть балки за­щемленной в том сечении, где определяется изгибающий мо­мент, мы освобождаем ее от всех фактически существующих опорных закреплений.

Рассмотрим ряд простейших примеров построения эпюр поперечных сил и изгибающих моментов.

Пример 1. Построить эпюры 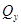и 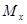для балки, изображённой на рисунке рис. 2.6.3.

Дата добавления: 2015-06-30