Тема 2.5. Кручение. 2 страница

2.5.3. При кручении бруса в его поперечных сечениях возникают только касательные напряжения. Теория кручения брусьев круглого сплошного или кольцевого поперечного сечения основана на ряде допущений, легко проверяемых экспериментально:

1) все поперечные сечения, плоские и нормальные до деформа­ции, остаются плоскими и нормальными после деформации (гипотеза Бернулли) и для определе­ния напряжений можно использовать метод плоских сечений;

2) расстояния между поперечными сечениями не изменяются, а следова­тельно, в поперечных сечениях отсутствуют продольные си­лы и нормальные напряжения;

радиусы поперечных сечений, остают­ся прямолинейными и поворачиваются вместе с сечениями на некоторый угол (рис. 2.5.4.).

Справедливость принятых допущений подтверждается тем, что полученные на их основе расчетные формулы для напряжений и перемещений хорошо подтверждаются экспе­риментально.

Формула для вычисления значения касательного напряжения в любой точке поперечного сечения бруса имеет вид:

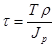, (2.5.1.)

где Т- крутящий момент в данном поперечном сечении (рис. 2.5.4.); 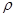- расстояние от оси бруса до данной точки; 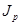- полярный момент инерции данного сечения. (см. п. 2.4.2.).

Из формулы (2.5.1.) следует, что:

касательные напряжения распределены вдоль любого радиуса сечения по линейному закону; эпюры касательных напряжений для круглого сплошного и кольцевого поперечных сечений показаны на рис. 2.5.5.;

в точках, равноудалённых от центра сечения, напряжения одинаковы;

наибольшие значения касательные напряжения достигают в точках контура поперечного сечения.:

.

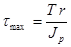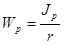Введя обозначение , получим следующее выражение для максимального касательного напряжения:

.

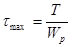Величину 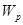называют полярным моментом сопротивления сечения. Его размерность 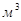. Очевидно, полярный момент сопротивления является геометрической характеристикой прочности бруса круглого поперечного сечения при кручении.

Для кольцевого сечения(рис. 2.4.5.)

;

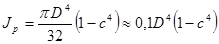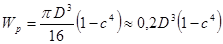, где .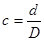

Для круглого сплошного сечения (рис. 2.4.4.)

;

.

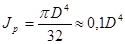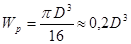2.5.3. Прочность бруса при кручении считают обеспеченной, если максимальное касательное напряжение в опасном сечении не превышает допускаемого. Условие прочности записыва­ют в виде

.

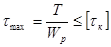При составлении условия прочности определяют положе­ние опасного сечения. Если все сечения бруса одинаковы, опасным является сечение, в котором возникает макси­мальный крутящий момент. Если крутящий момент во всех сечениях одинаков, опасным является сечение меньшего диаметра (с меньшим значением 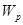).Если сечения бруса различны и различны крутящие моменты, расчет на проч­ность выполняют для нескольких сечений, имеющих малые диаметры и большие крутящие моменты.

Допускаемое касательное напряжение при кручении (чистом сдвиге) 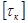выбирают в зависимости от допускае­мого для данного материала нормального напряжения при растяжении 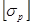. Для бруса из стали при­нимают 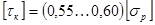; для чугуна .

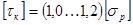Указанные значения допускаемых напряжений можно принимать лишь в случае чистого кручения. Практически на кручение обычно рассчитывают валы, которые помимо деформации кручения испытывают также изгиб. Не учитывая при ориентировочном расчёте валов влияние изгиба, делают ошибку, приводящую к уменьшению фактического коэффициента запаса прочности.

2.5.4. Рассмотрим брус, жёстко защемлённый одним концом и нагруженный на свободном конце скручивающим моментом М (рис. 2.5.4.).При деформации кручения бруса его поперечные сечения повёрнуты на некоторые углы по отношению к своему первоначальному положению или, что то же, по отношению к неподвижному сечению (заделке). Угол поворота будет тем больше, чем дальше отстоит данное сечение от заделки.

Вообще угол поворота произвольного сечения равен углу закручивания части бруса, заключённой между этим сечением и заделкой. Таким образом, угол поворота 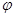торцового сечения представляет собой полный угол закручивания рассматриваемого бруса.

Угол закручивания элемента бруса длиной 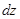(рис. 2.5.4.) крутящий момент Т и полярный момент инерции 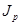постоянны, равен

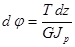, (2.5.2.)

где G- модуль упругости второго рода.

Полный угол закручивания бруса длиной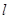

.

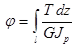Формула (2.5.2.) для определения угла закручивания бру­са по структуре аналогична формуле для определения деформации бруса при растяжении (сжатии) (см. п. 2.2.6.). Формула (2.5.2.) вы­ражает прямую пропорциональную зависимость между де­формацией и нагрузкой (закон Гука). Выражение 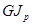назы­вают жесткостью сечения при кручении. Модуль сдвига G при этом характеризует жесткость материала, а полярный момент инерции является геометрической характеристикой жесткости сечения.

В самом общем случае, когда для отдельных участков бруса законы изменения крутящих моментов или полярных моментов инерции различны, следует пользоваться формулой

.

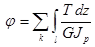2.5.6. В некоторых случаях работоспособность вала определя­ется не только его прочностью, но и жесткостью. В качестве примера можно указать на ходовые винты токарных станков, при деформации которых шаг их резьбы изменяется, а следовательно, и шаг резьбы, нарезанной на этом станке, получается с некоторой погрешностью. Задавая определенный допуск на точность изготовляемой резьбы, тем самым ставят требование ограничения угла закручивания ходового винта. Чем выше должна быть точность нарезанной резьбы, тем меньшую деформацию ходового винта можно допустить.

За меру жесткости при кручении принимают относительный угол закручивания (угол закручивания на единицу длины) вала, обозначаемый 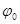. Из приведенного примера должно быть ясно, что в отличие от допускаемого напряжения, зависящего в первую очередь от материала вала, допускаемый угол закручивания зависит от на­значения вала.

Условие жесткости при кручении имеет вид

.

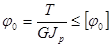При проектном расчете отсюда определяют требуемое зна­чение 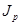, а затем вычисляют диа­метр вала.

Из двух значений диаметра вала, определенных из расчетов на прочность и жесткость, в качестве окончательного (исполнительного размера) должен быть, конечно, принят боль­ший.

В заключение остановимся на срав­нительной оценке валов круглого и кольцевого поперечных се­чений. Из эпюр касательных напряжений, приведенных на рис. 2.5.5., видно, что, удаляя материал вблизи оси вала, его прочность снижают весьма незначительно, так как эта часть материала для вала сплошного сечения мало нагружена. При равных площадях поперечного сечения, а следовательно, при одинаковой массе валов кольцевое сечение обладает большими полярными моментами инерции и сопротивления, чем сплош­ное, т. е. вал кольцевого сечения оказывается жестче и прочнее. Наконец, при равной прочности или равной жесткости, т. е. при одинаковых значениях 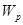или 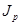, полый вал получается легче сплошного.

Дата добавления: 2015-06-30