Решение систем матричным методом

Квадратной матрицей 3-го порядка называется таблица из 3-х строчек и 3-х столбцов.

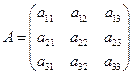. (7)

Внешне матрица 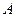похожа на определитель 3-го порядка, но определитель 3-го порядка - число, которое находится по формуле (1), а матрица 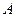- набор информации из девяти чисел, расположенных в виде (7). При написании они отличаются тем, что определитель по бокам имеет прямые линии, а матрица – скобки. Элементы матрицы 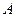и определителя 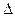называются одинаково: строки, столбцы, главная и побочная диагонали.

Введем определение единичной матрицы:

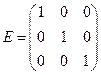. (8)

У единичной матрицы 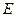на главной диагонали элементы равны 1, а все остальные элементы равны 0.

Матрицы можно транспонировать, т.е. из 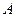образовать новую матрицу 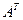,которая получается из 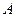путем замены строк соответствующими столбцами.

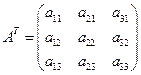. (9)

Две матрицы 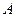и можно перемножать, в результате получим новую матрицу :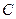

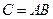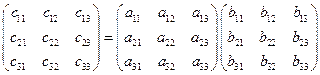; . (10)

Элементы матрицы 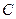находятся по правилу: если индексы 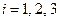и 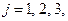то элемент 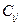равен сумме произведений элементов на 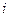-й строке матрицы 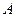на соответствующие элементы на 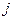-ом столбце матрицы .

Пример:

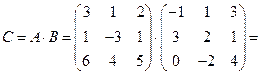
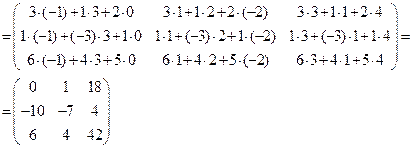
Далее понадобится понятие вектор – столбца. Обычно проекции вектора располагают строчкой 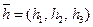. Если эти же проекции расположить вертикально, то получим вектор – столбец:

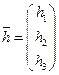. (11)

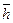Подобный вектор – столбец используется в произведении с матрицей. Произведением матрицы на вектор – столбец называется новый вектор 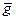элементы которого равны сумме произведений соответствующей строки матрицы на элементы вектора – столбца 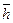, т. е.

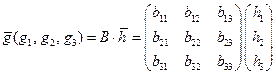, (12)

где 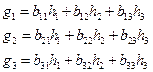. (13)

Еще необходимо определить обратную матрицу.

Матрица 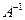называется обратной матрицей к матрице 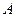, если имеют место следующие матричные равенства:

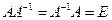. (14)

Для всякой матрицы 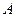, если ее определитель 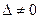, существует обратная матрица. Обратная матрица 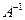строится следующим образом:

1. Вычисляем определитель 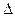данной матрицы .

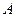2. Для элементов 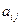матрицы 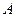вычисляем алгебраические дополнения 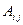по правилу: 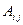равно определителю второго порядка взятого со знаком 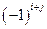и получаемого вычеркиванием 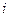-й строки и 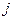-го столбца из определителя .

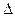Например:

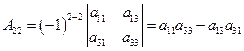
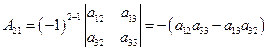
3. Из элементов 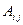составляем матрицу .

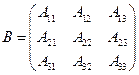. (15)

4. Каждый элемент матрицы делим на определитель 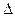и транспонируем полученную матрицу. В результате находим обратную матрицу:

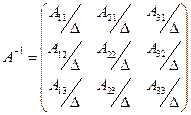. (16)

Пример вычисления обратной матрицы.

Найдем обратную матрицу для системы (6):

1. Определитель 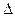данной матрицы уже найден 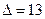. Так как 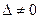, то обратная матрица существует.

2. Найдем алгебраические дополнения :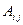

, ,

, ,

, ,

, ,

.

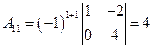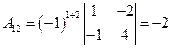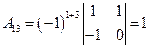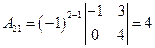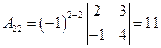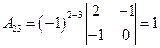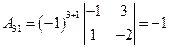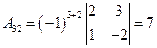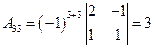3. Составим матрицу

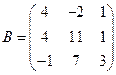
4. Найдем обратную матрицу :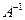

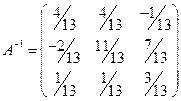. (17)

Проверку сделаем по формуле (14):

.

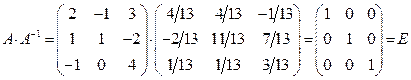Алгебраическую систему (2) можно записать в матричной форме

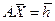(18)

где 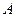– матрица из коэффициентов уравнений, 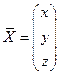– вектор – столбец из неизвестных, 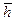– вектор – столбец из правых частей системы.

Если уравнение (18) слева умножить на 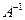, то получим решение системы (2) в виде

.

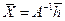Дата добавления: 2015-06-30