
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение. Решим систему (6) матричным методом
|
|
|
|
Пример
Решим систему (6) матричным методом. Обратная матрица для этой системы уже найдена (уравнение (17)). Поэтому сразу найдем 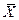 .
.
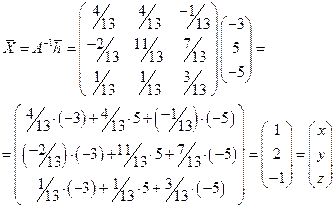
Ответ: 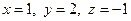 .
.
ЗАДАНИЕ 2
При выполнении второго задания контрольной работы необходимы следующие понятия векторной алгебры.
Вектором называется направленный отрезок. Вектор 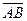 , заданный координатами начала
, заданный координатами начала 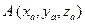 и конца
и конца 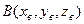 имеет проекции, равные разностям координат его конца и начала:
имеет проекции, равные разностям координат его конца и начала:
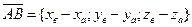
Его длина (модуль) определяется по формуле 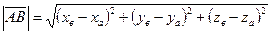 .
.
Проекция одного вектора 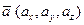 на направление другого
на направление другого 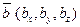 равна скалярному произведению этих векторов, деленному на модуль второго вектора:
равна скалярному произведению этих векторов, деленному на модуль второго вектора:
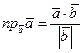
В координатной форме формула выглядит следующим образом:
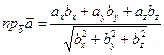 .
.
Угол a между положительными направлениями векторов 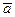 и
и 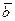 находится по формуле:
находится по формуле:
 ,
,
Значение 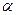 можно не искать в таблицах, а дать ответ в виде:
можно не искать в таблицах, а дать ответ в виде:
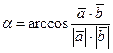 ,
,
Площадь треугольника АВС вычисляется при помощи векторного произведения по формуле:
 ,
,
где 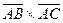 – векторное произведение.
– векторное произведение.
Пусть  и
и 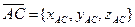 . Найдем их векторное произведение по формуле:
. Найдем их векторное произведение по формуле:
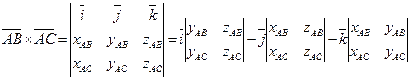
Вычислим длину вектора 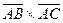 и возьмем ее половину, которая и будет численно равна искомой площади.
и возьмем ее половину, которая и будет численно равна искомой площади.
Объем пирамиды вычисляется как одна шестая абсолютной величины смешанного произведения трех векторов, на которых построена пирамида.
Пусть  ,
,  ,
, 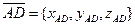 . Следует обратить внимание, что все три вектора
. Следует обратить внимание, что все три вектора  и
и  здесь выходят из одной точки А.
здесь выходят из одной точки А.
Их смешанное произведение равно:
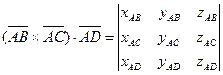 .
.
Объем пирамиды  будет равен одной шестой абсолютной величины произведения векторов:
будет равен одной шестой абсолютной величины произведения векторов:
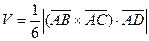 .
.
Пример. Даны координаты вершин пирамиды 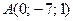 ,
, 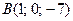 ,
, 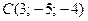 , и
, и  . Надо средствами векторной алгебры найти: 1) длину ребра
. Надо средствами векторной алгебры найти: 1) длину ребра 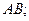 2) проекцию
2) проекцию  на
на  ; 3) угол между ребрами
; 3) угол между ребрами  и
и  ; 4) площадь грани
; 4) площадь грани 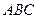 ; 5) объем пирамиды
; 5) объем пирамиды 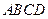 . Сделать чертёж.
. Сделать чертёж.
Решение: Сначала выполним чёртёж.

1) Найдем координаты вектора 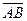
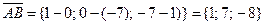 , тогда длина ребра
, тогда длина ребра  равна
равна 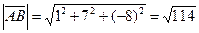 .
.
2) Найдем координаты векторов 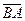 и
и  .
.
 ;
; 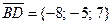 .
.
Вычислим проекцию  на
на  :
:
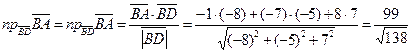 .
.
3) Найдем 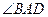 . Для этого вычислим координаты вектора
. Для этого вычислим координаты вектора 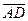 (координатывектора
(координатывектора 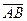 были получены ранее):
были получены ранее):
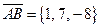 ,
, 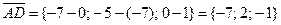 ,
,
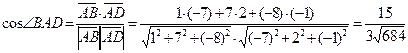 ,
,
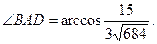
4) Для вычисления площади грани  возьмем любые два вектора, которые образуют эту грань, например
возьмем любые два вектора, которые образуют эту грань, например 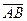 и
и 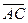 . Координаты вектора
. Координаты вектора
 .
.
Найдем векторное произведение 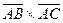

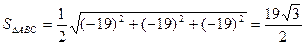 ед2.
ед2.
5). Координаты векторов 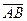 ,
, 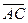 и
и 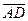 найдены выше. Вычислим их смешанное произведение:
найдены выше. Вычислим их смешанное произведение:
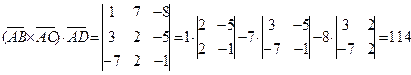
Объем пирамиды равен 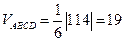 ед3.
ед3.
ЗАДАНИЕ 3
Для выполнения третьего задания рассмотрим линии первого порядка  – уравнение прямой в общем виде.
– уравнение прямой в общем виде.
Уравнение прямой, проходящей через сторону АВ треугольника АВС, найдем как уравнение прямой, проходящей через две точки 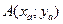 и
и 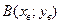 :
:
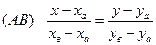 .
.
Аналогично найдем уравнения сторон  и
и 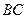 .
.
Чтобы написать уравнение медианы 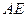 , вспомним, что точка
, вспомним, что точка 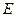 делит сторону
делит сторону 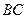 пополам. Найдем координаты точки
пополам. Найдем координаты точки 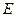 . Если
. Если 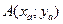 ,
,  ,
, 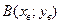 и
и  , то
, то
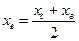 ,
, 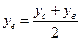 .
.
Теперь осталось только записать уравнение прямой 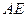 , проходящей через две точки
, проходящей через две точки 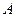 и
и 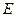 .
.
Высота 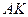 перпендикулярна стороне
перпендикулярна стороне 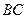 . Через
. Через 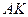 проведем прямую с угловым коэффициентом
проведем прямую с угловым коэффициентом 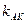 :
:
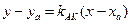 . (19)
. (19)
Так как 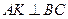 , то из условия перпендикулярности двух прямых имеем
, то из условия перпендикулярности двух прямых имеем
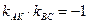 . (20)
. (20)
Запишем уравнение стороны 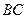 в виде с угловым коэффициентом
в виде с угловым коэффициентом
 .
.
Из этого уравнения определим 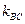 , а из (20) найдем
, а из (20) найдем 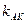 . Зная угловой коэффициент прямой
. Зная угловой коэффициент прямой 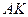 из (19) получим уравнение перпендикуляра
из (19) получим уравнение перпендикуляра 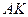 .
.
Длину высоты найдем как расстояние от точки 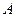 до прямой
до прямой 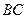 по формуле:
по формуле:
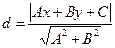 ,
,
где  – уравнение стороны
– уравнение стороны 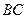 .
.
Чтобы найти внутренние углы треугольника 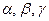 нужно угловые коэффициенты сторон выписать в порядке убывания:
нужно угловые коэффициенты сторон выписать в порядке убывания: 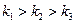 , затем вычислить тангенсы углов по формулам:
, затем вычислить тангенсы углов по формулам:
 ,
,  ,
, 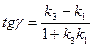 .
.
Пример. Даны координаты вершин треугольника: 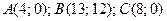 . Требуется найти: 1) уравнение сторон треугольника; 2) уравнение медианы
. Требуется найти: 1) уравнение сторон треугольника; 2) уравнение медианы 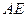 ; 3) длину и уравнение высоты
; 3) длину и уравнение высоты 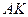 ; 4) внутренние углы треугольника
; 4) внутренние углы треугольника 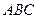 .
.
Решение:
1) Найдем уравнение стороны  :
:  . Запишем уравнение в общем виде:
. Запишем уравнение в общем виде:  .
.
Найдем уравнение  :
:  или
или 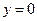 .
.
Найдем уравнение 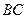 :
:  ; т. е.
; т. е. 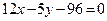 .
.
2) Найдем координаты точки 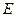 :
:
 ;
; 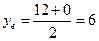 ;
; 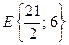 .
.
Запишем уравнение 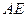 :
:
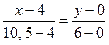 , или
, или 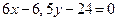 .
.
3) Найдем длину высоты АК
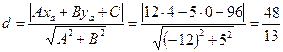 .
.
Придадим уравнению прямой ВС форму уравнения с угловым коэффициентом 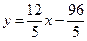 , откуда
, откуда 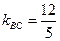 .
.
Угловой коэффициентом прямой АК равен 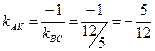 .
.
Уравнение (АК): 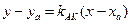 ;
;
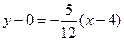 ;
; 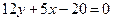 .
.

Рис. 1. Чертеж к заданию 3.
4) Запишем уравнения сторон треугольника в виде уравнений прямых с угловыми коэффициентом:
(АС): 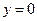 ,
, 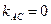 .
.
(АВ): 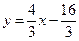 ,
, 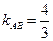 .
.
(ВС): 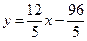 ,
, 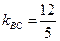 .
.
 ,
, 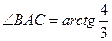 .
.
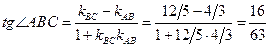 ,
, 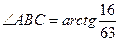 .
.
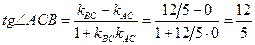 ,
, 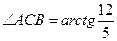 .
.
Задание 4
Окружностью называется геометрическое место точек плоскости, равноудаленных от данной точки, называемой центром. Расстояние 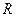 от точек окружности до центра называется радиусом.
от точек окружности до центра называется радиусом.
Уравнением окружности радиуса R с центром в начале координат является выражение
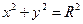 .
.
Если центр окружности находится не в начале координат, а в произвольной точке 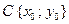 , то ее уравнение имеет вид
, то ее уравнение имеет вид
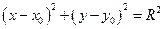 . (21)
. (21)
Раскрывая скобки в (21) получим
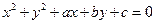 . (22)
. (22)
Чтобы от уравнения (22) перейти к (21) нужно применить метод выделения полного квадрата. Рассмотрим алгоритм этих преобразований.
Дана окружность 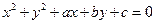 .
.
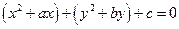 .
.
 .
.
 .
.
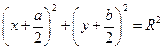 ,
,
где 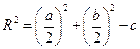 .
.
Получили уравнение окружности с центром в т. 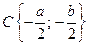 и радиусом R в системе координат
и радиусом R в системе координат 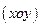 .
.
Обозначая 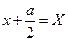 , а
, а 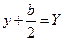 будем иметь уравнение окружности в новой системе координат
будем иметь уравнение окружности в новой системе координат 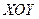
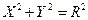 .
.
Центр ее находится в т. 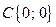 , радиус равен R.
, радиус равен R.
Пример. Дано уравнение окружности 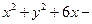
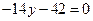 . Методом выделения полного квадрата привести его к виду
. Методом выделения полного квадрата привести его к виду 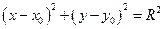 . Путем параллельного переноса системы координат привести последнее уравнение к виду
. Путем параллельного переноса системы координат привести последнее уравнение к виду 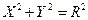 . Построить обе системы координат, найти в каждой из них центр окружности. Сделать чертеж.
. Построить обе системы координат, найти в каждой из них центр окружности. Сделать чертеж.
Решение.  .
.
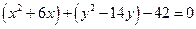
 .
.
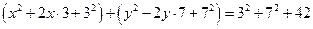 .
.
 .
.
Центр окружности находится в т.  , радиус равен 10. Введем новые переменные
, радиус равен 10. Введем новые переменные 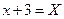 и
и 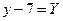 , тогда в новой системе координат
, тогда в новой системе координат 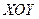 окружность примет вид
окружность примет вид 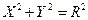 . Центр ее совпадает с началом координат.
. Центр ее совпадает с началом координат.
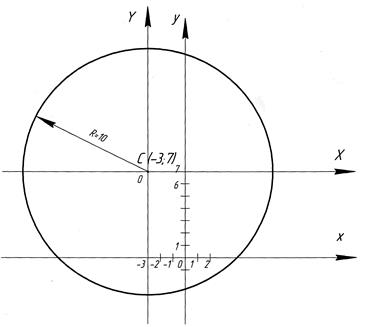
Рис. 2. Чертеж к заданию 4.
Задание 5
В этом задании рассматриваются вопросы аналитической геометрии в пространстве.
1) Уравнение плоскости, проходящей через три данные точки  ;
; 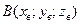 ;
;  находятся по формуле
находятся по формуле
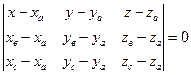 .
.
Ответ нужно представить в общем виде уравнения плоскости
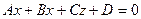 .
.
2) Для отыскания угла между прямой и плоскостью нужно:
а) написать уравнение прямой, проходящей через две данные точки:  и
и 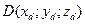 , по формуле:
, по формуле:
 . (23)
. (23)
Направляющий вектор этой прямой 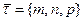 имеет координаты
имеет координаты
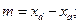
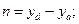
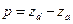 .
.
б) угол 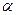 между прямой и плоскостью в пространстве находится по формуле:
между прямой и плоскостью в пространстве находится по формуле:
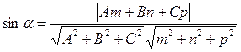 ;
;
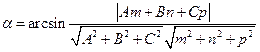 ,
,
где 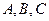 - координаты нормального вектора
- координаты нормального вектора 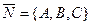 берутся из общего уравнения плоскости
берутся из общего уравнения плоскости 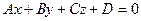 , как коэффициенты перед
, как коэффициенты перед 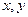 и
и  соответствено.
соответствено.
3) Уравнение прямой, проходящей через две точки, было приведено ранее (23).
4) Для того, чтобы найти уравнения высоты пирамиды, опущенной из точки 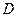 на грань
на грань 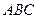 , удобно воспользоваться каноническими уравнениями прямой в пространстве
, удобно воспользоваться каноническими уравнениями прямой в пространстве
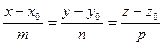 ,
,
где  – координаты точки, лежащей на прямой. В данном случае нам известны координаты точки
– координаты точки, лежащей на прямой. В данном случае нам известны координаты точки  . Проекции направляющего вектора
. Проекции направляющего вектора 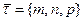 найдем из условия перпендикулярности прямой и плоскости. Так как вектор нормали
найдем из условия перпендикулярности прямой и плоскости. Так как вектор нормали 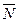 к плоскости и направляющий вектор
к плоскости и направляющий вектор 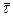 прямой параллельны, то в качестве направляющего вектора можно взять вектор
прямой параллельны, то в качестве направляющего вектора можно взять вектор 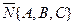 , т.е.
, т.е. 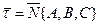 .
.
5) Основанием высоты является точка пересечения прямой, проходящей через высоту, с плоскостью основания 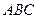 . Для нахождения этой точки пересечения решим систему уравнений:
. Для нахождения этой точки пересечения решим систему уравнений:
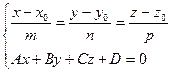
Эту систему удобно решать, если перейти к уравнению прямой в параметрическом виде
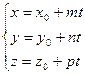 (*)
(*)
Подставим выраженные переменные 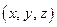 через
через 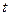 из (*) в уравнение плоскости
из (*) в уравнение плоскости
 .
.
Отсюда найдем параметр t, подставим его в уравнение прямой и получим координаты искомой точки пересечения прямой с плоскостью.
Пример. В пирамиде из задания 2 найти: 1) уравнение плоскости АВС; 2) угол между ребром AD и гранью АВС; 3) уравнение прямой АВ; 4) уравнение высоты, опущенной из вершины D на грань АВС; 5) основание этой высоты.
1) уравнение плоскости выразим через определитель
 .
.
Решив его, получим уравнение грани (АВС) 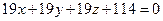 . Отсюда находим вектор нормали
. Отсюда находим вектор нормали 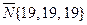 . (24)
. (24)
2) Для вычисления угла между ребром 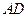 и гранью АВС запишем сначала каноническое уравнение ребра
и гранью АВС запишем сначала каноническое уравнение ребра 
 .
.
Уравнение прямой  :
:  .
.
Координаты направляющего вектора вдоль 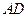
 . Координаты нормали
. Координаты нормали 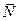 найдены выше (24).
найдены выше (24).
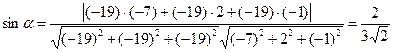 .
.
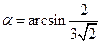 .
.
3) Уравнение прямой  :
:
 .
.
После упрощения имеем -  .
.
Координаты направляющего вектора вдоль  -
-  .
.
4) Найдем уравнение высоты, опущенной из вершины 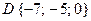 на грань АВС, уравнение которой получено ранее в (24).
на грань АВС, уравнение которой получено ранее в (24).
Так как  , то возьмем вектор
, то возьмем вектор 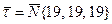 , тогда уравнение высоты
, тогда уравнение высоты 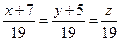 .
.
5) Решив систему уравнений
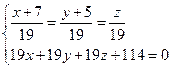 ,
,
найдем точку К, которая будет являться основанием высоты, опущенной из вершины D на грань АВС.
Для этого запишем уравнение прямой в параметрическом виде
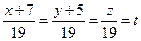 ,
, 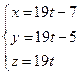 . (25)
. (25)
Подставим в уравнение плоскости вместо переменных x, y, z их выражения через параметр 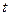 :
:
 ,
,
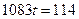 ,
, 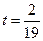 . (26)
. (26)
Теперь из (25) найдем x, y, z.
 , т. К {-5; -3; 2}.
, т. К {-5; -3; 2}.
ЗАДАНИЕ 6
В данном задании требуется вычислить пределы, не пользуясь правилом Лопиталя. Для этого рассмотрим некоторые теоретические сведения.
Если функция 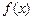 в окрестности точки
в окрестности точки 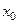 определена и непрерывна, то ее предел можно вычислить по формуле:
определена и непрерывна, то ее предел можно вычислить по формуле:
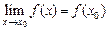
Поэтому при вычислении пределов надо вначале убедиться, является ли функция 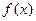 непрерывной, или она разрывная в окрестности точки
непрерывной, или она разрывная в окрестности точки 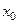 путем прямой подстановки
путем прямой подстановки  в выражение функции
в выражение функции 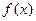 . Если
. Если 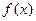 не существует при
не существует при  , то тогда следует находить предел
, то тогда следует находить предел 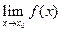 . Для этого применяют специальные приемы.
. Для этого применяют специальные приемы.
Разрывные функции часто имеют неопределенные значения в точке разрыва  . Неопределенности бывают следующих типов 1)
. Неопределенности бывают следующих типов 1) 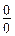 2)
2) 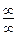 3)
3)  4)
4) 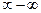 5)
5) 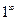 . Это – символическое обозначение неопределенностей. Если функция имеет вид дроби
. Это – символическое обозначение неопределенностей. Если функция имеет вид дроби  , у которой при
, у которой при  числитель и знаменатель одновременно обращаются в ноль, т. е.
числитель и знаменатель одновременно обращаются в ноль, т. е.  и
и 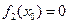 , то такая неопределенность обозначается
, то такая неопределенность обозначается 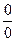 . Если же при
. Если же при 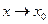 имеем
имеем 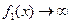 и
и 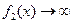 одновременно, то неопределенность обозначается
одновременно, то неопределенность обозначается 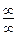 . Функция может иметь вид произведения
. Функция может иметь вид произведения  . Если при этом
. Если при этом  и при
и при 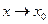
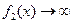 , то такую неопределенность обозначают
, то такую неопределенность обозначают  . Возможен случай, когда функция имеет вид разности
. Возможен случай, когда функция имеет вид разности  , причем при
, причем при 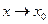
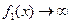 и
и 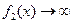 одновременно. Здесь возникает неопределенность типа
одновременно. Здесь возникает неопределенность типа 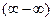 . Еще может быть вариант, когда функция имеет вид
. Еще может быть вариант, когда функция имеет вид 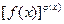 и
и 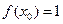 , а при
, а при 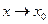
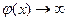 . Такая неопределенность обозначается
. Такая неопределенность обозначается 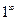 . Для раскрытия подобных неопределенностей применяются специальные преобразования, которые допустимы правилами математики. После этого получаем выражения без неопределенностей и можно будет вычислить предел.
. Для раскрытия подобных неопределенностей применяются специальные преобразования, которые допустимы правилами математики. После этого получаем выражения без неопределенностей и можно будет вычислить предел.
Для случая, когда 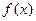 имеет вид рациональной дроби и
имеет вид рациональной дроби и 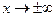 , имеем неопределенность типа
, имеем неопределенность типа  , для вычисления которой надо числитель и знаменатель дроби поделить на старшую степень знаменателя.
, для вычисления которой надо числитель и знаменатель дроби поделить на старшую степень знаменателя.
Пример для задания а): 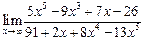 . Имеем неопределенность вида
. Имеем неопределенность вида  . Чтобы раскрыть эту неопределенность разделим числитель и знаменатель на
. Чтобы раскрыть эту неопределенность разделим числитель и знаменатель на 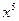 .Получим
.Получим 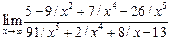 . Так как при
. Так как при 

 , то имеем
, то имеем 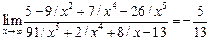 .
.
Во втором примере функция имеет вид дроби 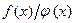 , у которой числителем и знаменателем являются рациональные выражения, которые содержат только целые положительные степени переменной
, у которой числителем и знаменателем являются рациональные выражения, которые содержат только целые положительные степени переменной  . Если при
. Если при  числитель
числитель  и знаменатель
и знаменатель 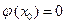 , то
, то 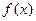 и
и  нацело (без остатка) делятся на разность (
нацело (без остатка) делятся на разность (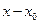 ). Это деление осуществляется углом.
). Это деление осуществляется углом.
Пример для задания б):  . Так при
. Так при 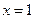 имеем
имеем 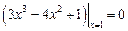 и
и 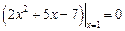 , то
, то
|
|
|
|
|
Дата добавления: 2015-06-30; Просмотров: 608; Нарушение авторских прав?; Мы поможем в написании вашей работы!