Понятие функции алгебры логики

ВВЕДЕНИЕ

Березняцкий Ю.Ф.

Гомель 2004

ФУНКЦИЙ АЛГЕБРЫ ЛОГИКИ

Пособие для практических занятий
по дисциплине «Теория дискретных устройств»

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

«БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТРАНСПОРТА»

Кафедра автоматики и телемеханики

Ю. Ф. БЕРЕЗНЯЦКИЙ

ЗАДАНИЕ И МИНИМИЗАЦИЯ

ФУНКЦИЙ АЛГЕБРЫ ЛОГИКИ

Пособие для практических занятий

по дисциплине «Теория дискретных устройств»

Одобрено методической комиссией

электротехнического факультета

Гомель 2004

УДК 656.25-192

Б866

Р е ц е н з е н т – канд. физ.-мат. наук, зав. кафедрой «Микропроцессорная техника и информационно-управляющие системы» Н.В. Рязанцева

Б866 Задание и минимизация функций алгебры логики: Пособие для практических занятий по дисциплине «Теория дискретных устройств». – Гомель: БелГУТ, 2004. – 44 с.

Рассматриваются вопросы задания и минимизации полностью и неполностью заданных функций алгебры логики при помощи законов алгебры логики, карт Карно, методами Квайна, Квайна–Мак-Класки и существенных переменных.

Предназначено для студентов электротехнического факультета и ФБО в качестве руководства по минимизации функций алгебры логики при выполнении практических занятий. Пособие также может использоваться студентами при выполнении курсового проекта по дисциплине «Теория дискретных устройств».

УДК 656.25-192

© Ю.Ф. Березняцкий, 2004.

Современные системы автоматики, телемеханики и связи (АТ и С) имеют преимущественно электронное, микроэлектронное и микропроцессорное исполнение. Подавляющее большинство выпускаемых промышленностью и разрабатываемых систем АТ и С являются дискретными.

Поэтому для успешного усвоения принципов их функционирования и анализа работы необходимы знания в области теории дискретных устройств (ТДУ). ТДУ – это дисциплина, изучающая принципы анализа и синтеза устройств, построенных на базе дискретных элементов (ДЭ). Под дискретным элементом понимается минимальная совокупность деталей, объединенных в общую схему для выполнения заданной функции и меняющих свое выходное значение скачкообразно при определенном изменении входной величины. К простейшим ДЭ относятся реле, диоды, транзисторы, тиристоры и т.д.

Данное пособие дает основные навыки по применению основных аксиом и законов алгебры логики в ТДУ, что позволяет в конечном итоге реализовывать схемы дискретных устройств наиболее оптимальным образом.

Большая часть методов анализа и синтеза всех классов дискретных устройств основана на применении положений алгебры логики (АЛ) [1–4]. АЛ является разделом математической логики. В АЛ все операции проводятся с переменными, принимающими лишь два значения – «истина» и «ложь». Для теории дискретных устройств значение «истина» соответствует логической единице «1», а значение «ложь» – логическому нулю «0». Поэтому АЛ называют еще двухзначной или булевой, по фамилии ее основоположника ирландского математика Дж. Буля (1815–1864) [3].

Возможность применения АЛ для синтеза и анализа реальных дискретных устройств (ДУ) обусловлена использованием в них двоичных сигналов и двустабильных элементов, имеющих два четко выраженных состояния. Например, состояние реле соответствует «1», если оно находится под током, а если реле обесточено – его состояние соответствует «0».

В теории дискретных устройств (ТДУ) часто оперируют таким понятием, как функция алгебры логики (ФАЛ) [1, 3, 4].

Функция 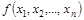называется ФАЛ в том случае, если она и ее переменные могут принимать лишь два взаимоисключающих значения «0» и «1».

Переменные ФАЛ (ее аргументы) сопоставляют со значениями сигналов на входах ДУ, а значения ФАЛ (ее результат) – со значениями сигналов на выходах ДУ.

Поскольку реальные ДУ имеют конечное число входов, то мы будем рассматривать функции конечного числа аргументов. Для n двоичных переменных x ₁, x ₂, …, x _n существует k = 2ⁿ наборов значений переменных и R = 2^k различных ФАЛ. Например, для одного аргумента x ₁ существует k = 2¹ = 2 набора переменных { x ₁ = 0, x ₁ = 1} и R = 2² = 4 функции алгебры логики f ₀ = 0 (константа нуль), f ₁ = 1 (константа единица), f ₂ = x ₁ (повторение x ₁) и 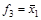(инверсия x ₁, т.е. замена всех его значений на обратные).

Так как число аргументов и число значений каждого аргумента конечны, конечна и область определения любой ФАЛ.

Дата добавления: 2015-07-02