
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Оценка точности результатов измерений по значениям невязок фигур и свободных членов синусных условий
|
|
|
|
Составление таблицы направлений, приведенных к центрам пунктов и редуцированных на плоскость в проекции Гаусса-Крюгера
Вычисление приведенных к центрам пунктов и редуцированных на плоскость в проекции Гаусса-Крюгера направлений производится в таблице 7.
Для заполнения столбцов 1, 2, 3 используются значения измеренных на пунктах триангуляции направлений (таблица 3). Поправки за центрировку и редукцию для каждого из измеренных направлений вычисляют по формулам (5) и выписывают, соответственно, в столбцы 4 и 5 из таблицы 5. В столбец 6 заносят вычисленные по формуле (7) значения поправки за кривизну изображения геодезической линии на плоскости с учетом знака. Следует обратить внимание на правильность введения поправки за редукцию визирной цели, которая вводится со своим знаком в обратное направление (столбец 5 табл.7), например, в направление 1-2 вводится поправка r², вычисленная на пункте 2 для направления на пункт 1.
Среднее значение измеренного направления исправляют поправками с², r²,  по формуле:
по формуле:
 ,
,
где  - приведенные к центрам пунктов и редуцированные на плоскость проекции направления;
- приведенные к центрам пунктов и редуцированные на плоскость проекции направления;  – измеренные направления;
– измеренные направления;
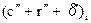 -суммарная поправка за центрировку, редукцию и кривизну изображения геодезической линии для направления
-суммарная поправка за центрировку, редукцию и кривизну изображения геодезической линии для направления 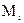 ;
;
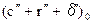 , - суммарная поправка в исходное направление.
, - суммарная поправка в исходное направление.
Таблица 7
Таблица направлений, приведенных к центрам пунктов и редуцированных на плоскость в проекции Гаусса-Крюгера
| Назв. пункта | Назв. напр | Измеренное направление M ° ¢ ² | c" | r" | 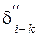
| (c+r + 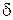 )
² )
²
| (c+r+ 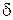 )- (c+r+ )- (c+r+ 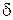 )0
² )0
²
| Приведён. направление М¢ ° ¢ ² | ||||
| 0,0 | -1,4 | +0,2 | -1,2 | |||||||||
| 50,9 | +4,8 | +0,1 | +4,9 | +6,1 | 57,0 | |||||||
| 23,5 | +55,5 | -0,4 | +55,1 | +56,3 | 19,8 | |||||||
| 0,0 | +0,2 | +0,2 | ||||||||||
| 35,4 | +24,5 | -0,1 | +24,4 | +24,2 | 59,6 | |||||||
| 39,2 | +13,1 | -0,2 | +12,9 | +12,7 | 51,9 | |||||||
| 0,0 | +0,1 | -0,5 | -0,4 | |||||||||
| 27,4 | -0,4 | -0,4 | 27,4 | |||||||||
| 18,3 | +0,3 | -0,2 | +0,1 | +0,5 | 18,8 | |||||||
| 0,0 | -1,4 | -0,5 | -1,9 | |||||||||
| 23,1 | -3,4 | +0,2 | -3,2 | -1,3 | 21,8 | |||||||
| 16,6 | +0,5 | +0,5 | +2,4 | 19,0 | ||||||||
| 0,0 | -0,2 | +0,5 | +0,3 | |||||||||
| 4,0 | -34,6 | +0,2 | -34,4 | -34,7 | 29,3 | |||||||
| 15,9 | -3,4 | +0,7 | -2,7 | -3.0 | 12,9 | |||||||
| 0,0 | +1,2 | +19,8 | +0,4 | +21,4 | ||||||||
| 44,1 | +1,5 | -7,1 | +0,4 | -5,2 | -26,6 | 17,5 | ||||||
| 00,9 | -0,3 | -0,3 | -0,2 | -0,8 | -22,2 | 38,7 | ||||||
| 0,0 | +35,8 | -0,1 | +35,7 | |||||||||
| 53,8 | -4,3 | +0,1 | -4,2 | -39,9 | 13,9 | |||||||
| 59,5 | +0,4 | +0,4 | -35,3 | 24,2 | ||||||||
| 36,1 | -0,1 | -0,2 | -0,3 | -36,0 | 00,1 | |||||||
| 23,6 | -0,4 | -0,7 | -1,1 | -36,8 | 46,8 | |||||||
| 36,1 | +43,8 | -0,4 | +43,4 | 7,7 | 43,8 |
Пример:
Для пункта 1 суммарная поправка в исходное направление 1-2 и исправленное значение направления 1-7составляют:
 ,
,

Качество угловых измерений в триангуляции характеризуется средней квадратической ошибкой измеренного угла, вычисляемой по невязкам треугольников и синусных условий. Для этого по приведенным к центрам пунктов и на плоскость в проекции Гаусса-Крюгера направлениям вычисляют углы в треугольниках и подсчитывают их невязки (табл. 8) по формуле (4).
Предельные невязки в треугольниках, вычисляемые по формуле
 ,
,
не должны превышать ± 20˝ при средней квадратической ошибке измерения углов в триангуляции данного класса 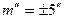 .
.
Среднюю квадратическую ошибку измерения угла по невязкам треугольников вычисляют по формуле Ферерро:
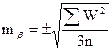 ,
,
где  - сумма квадратов невязок треугольников, n – число треугольников.
- сумма квадратов невязок треугольников, n – число треугольников.
К синусным относят полюсные и базисные условия, возникающие в сети триангуляции.
Полюсные условия возникают в центральных системах и там, где в сети имеются диагонали (геодезические четырехугольники).
В данной сети полюсное условие возникает в центральной системе с полюсом на пункте 7. Свободные члены этого условия вычислены в таблице 9.
Таблица 8
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 729; Нарушение авторских прав?; Мы поможем в написании вашей работы!