Пример. Вычисление невязок треугольников

Вычисление невязок треугольников

№ треуголь-ника	Назв. верш.	Угол	W, сек	№ треуголь-ника	Назв. верш.	Угол	W, сек
°	¢	²	°	¢	²
				52,3						47,1
I				13,9		IV				46,7
				57,0						21,8
	S			03,2	+3,2		S			55,6	-4,4
				10,3						21,2
II				51,4		V				57,0
				59,6						43,6
	S			01,3	+1,3		S			01,8	+1,8
				57,2						22,8
III				35,9		VI				16,2
				27,4						17,5
	S			00,5	+0,5		S			56,5	-3,5

.

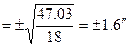Полюсное условие, выраженное через синусы углов, имеет вид:

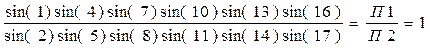. (8)

Свободный член полюсного условия вычисляется по формуле:

,

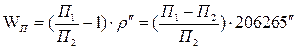где - соответственно, произведения синусов углов числителя и знаменателя дроби полюсного условия, не должен превышать значения , которое вычисляется по формуле:

.

.

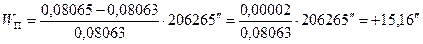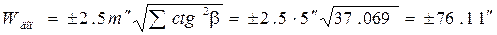
Базисное условие возникает в сети триангуляции, если имеются две или более стороны, длины которых известны (измерены или вычислены по известным координатам). В сети триангуляции, изображенной на рис. 1.1, известны длины базисных сторон между пунктами 2-3 - и пунктами 4-5 - .

Для составления базисного условия вычисляют по теореме синусов последовательно связующие стороны треугольников II, III, IV, начиная от известной стороны :

; ; .

После объединения формул в одну получаем:

.

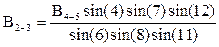Свободный член базисного условия, вычисляемый по формуле

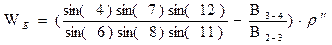, (9)

не должен превышать допустимого значения .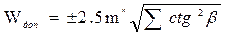

Вычисления представлены в таблице 10.

В том случае, когда свободный член какого либо условного уравнения не удовлетворяет установленным допускам, необходимо выявить и устранить причины, приведшие к недопустимой величине.

Если угловые измерения в сети не содержат недопустимых ошибок, выполнены качественно и удовлетворяют предъявляемым к ним требованиям, можно приступать к окончательному уравниванию сети триангуляции.

Таблица 9

	Вычисление коэффициентов и свободного члена полюсного условного уравнения
Угол при вершине треугольника	Значение угла ° ¢ ²	Sin β	ctg β	ctg^2 β
			57,0	0,47484	+1,853	3,435
			59,6	0,97305	-0,237	0,056
			27,4	0,99184	+0,129	0,017
			21,8	0,98593	-0,170	0,029
			43,6	0,38100	+2,427	5,889
			17,5	0,46852	+1,886	3,556
Числитель П1 =	0,08065
			52,3	0,79563	+0,761	0,580
			51,4	0,21015	+4,652	21,644
			57,2	0,74933	+0,884	0,781
			47,1	0,77490	+0,816	0,665
			21,2	0,87216	-0,561	0,315
			22,8	0,95225	+0,321	0,103
Знаменатель П2 =	0,08063
W П=	+51,16²				[ctg^2β]=	37,069
W доп=	±76,11²

Вывод: Значение невязки полюсного условия не превосходит допустимого значения.

Таблица 10

Дата добавления: 2015-07-02