Краткие сведения из алгоритма способа. Уравнивание триангуляции коррелатным способом

Уравнивание триангуляции коррелатным способом

Базисного условного уравнения

Вычисление коэффициентов и свободного члена

Угол при вершине треугольника	Значение угла ° ¢ ²	Sin β	ctg β	ctg^2 β
			59,6	0,973045	-0,237	0,056
			27,4	0,991837	+0,129	0,017
			46,7	0,493633	+1,762	3,104
Числитель П1	0,476406
			10,3	0,902857	+0,476	0,227
			57,2	0,749332	+0,884	0,781
			47,1	0,774905	+0,816	0,665
Знаменатель П2	0,524254
W Б=	-5,1”				[ctg^2β] =	4,850
W доп=	±27,53”

Вывод: Значение невязки базисного условия не превосходит допустимого значения.

Конечной целью уравнительных вычислений является определение вероятнейших координат определяемых пунктов геодезической сети, вычисление поправок к измеренным величинам и оценка точности.

Уравнительные вычисления выполняются на основе метода наименьших квадратов под условием .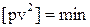

Студенту предлагается выполнить уравнивание геодезической сети триангуляции 1 разряда коррелатным способом. Схема сети представлена на рисунке 1.1. Исходные величины (координаты исходного пункта, исходный дирекционный угол, значения базисных сторон) представлены в таблице 3. Значения приведенных к центрам пунктов и редуцированных на плоскость в проекции Гаусса-Крюгера измеренных в сети направлений представлены в таблице 7.

Процесс уравнивания сети триангуляции корреллатным способом заключается в следующем.

1. В качестве уравниваемых величин принимают измеренные величины (углы 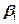, где i =1,…, N; N – количество измеренных углов в сети).

2. Наличие в геодезической сети точных математических зависимостей позволяет составить систему условных уравнений вида 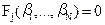, после чего вычисляют их свободные члены по формуле 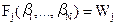. Затем вычисляют коэффициенты условных уравнений поправок, т.е. условных уравнений, приведенных к линейному виду, 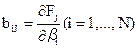. В матричной форме записи система приведенных к линейному виду условных уравнений имеет вид: ,

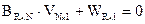где В_RxN - матрица коэффициентов условных уравнений, состоящая из R - строк (количество условных уравнений) и N - столбцов (количество измеренных углов в сети), V_Nx1 - вектор поправок к измеренным элементам, W_Rx1 - вектор невязок.

3. Решают систему уравнений по методу наименьших квадратов с оценкой всех неизвестных. С этой целью составляют нормальные уравнения коррелат ,

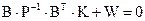где Р - веса измерений, К - вектор коррелат.

Решение системы имеет вид:

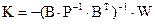. (10)

С помощью вектора коррелат вычисляют вектор поправок по формуле

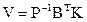. (11)

Уравненные углы получают путем исправления поправками соответствующих измеренных значений.

Используя уравненные величины углов, вычисляют координаты определяемых пунктов и составляют каталог координат. Среднюю квадратическую ошибку измерений (ошибку единицы веса) получают по результатам уравнивания по формуле

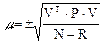. (12)

Дата добавления: 2015-07-02