Напор и расход рабочего колеса при конечном числе

Течение воды в каналах рабочего колеса и основное уравнение работы центробежных насосов (уравнение Эйлера)

КРАТКАЯ ТЕОРИЯ ЦЕНТРОБЕЖНЫХ НАСОСОВ

Как известно из конструкции насосов, рабочее колесо состоит из двух дисков, соединенных между собой криволинейными лопатками (на рис. 6.1 передний диск отсутствует). Диски и лопатки образуют проточные каналы, по которым движется жидкость от центра к периферии за счет воздействия на нее центробежной силы при вращении рабочего колеса. Таким образом в наличии поступательное движение

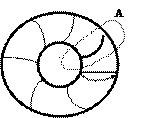Рис.6.1. Рабочее колесо

центробежного насоса

жидкости, которая одновременно и вращается. Такое сложное движение затрудняет его математическое описание.

В связи с этим прмем следующие условия:

1) количество лопаток рабочего колеса стремится к бесконечности;

2) по каналам протекает идеальная жидкость.

Соблюдение этих условий позволяет рассматривать каждый канал бесконечно малых размеров, по которым протекают элементарные струйки идеальной жидкости, где отсутствуют силы трения.

Для получения теоретического уравнения работы центробежного насоса из условного рабочего колеса с бесконечно большим количеством лопаток вырежем одну из них (фрагмент А на рис.6.1) и поместим ее отдельно (рис.6.2).Каждая частица жидкости, попадая на начало лопатки, обладает абсолютной скоростью С₁,которую можно разложить на два вектора: U₁ - окружную и W₁ - относительную в виде параллелограмма скоростей на входе в проточный канал.

На конце лопатки каждая частица жидкости уже будет обладать другой абсолютной скоростью С₂, которая разлагается тоже в виде параллелограмма на векторы: U₂ - окружная скорость на выходе и W₂ - относительная скорость на выходе. Так как скорость частиц меняется от С₁ до С₂, то изменение момента количества движения можно записать в виде:

DМ = М₂ - М₁,

где М₂ - момент количества движения элементарной массы жидкости m, обладающей скоростью С₂, а М₁ - момент количества движения той же массы m, обладающей скоростью С₁.

Из теоретической механики известно, что момент количества движения равен произведению массы на скорость и на плечо, т.е. расстоянию от вектора скорости до точки, относительно которой определяется момент. Значит

М = m · С· h. (6.1)

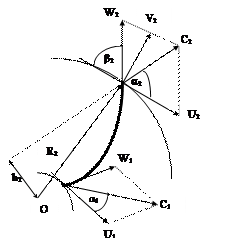Рис.6.2. Фрагмент А (рис.6.1)

Если определять момент количества движения относительно центра рабочего колеса (т.О на рис.6.2),то необходимо опустить из него перпендикуляр на продолжение вектора скорости. На рис.6.2 продлен вектор С₂ и из точки О опущен перпендикуляр h₂, который образовал с радиусом R₂ угол a₂, равный углу между векторами U₂ и С₂ из-за перпендикулярности сторон. Значит h₂ = R₂ cosa₂.

Учитывая все это, момент количества движения на выходе из канала будет равен

М₂= m · C₂ · h₂ = m · C₂ · R₂ cos a_2..

Поступая аналогичным образом для массы жидкости на входе, получим момент количества движения относительно той же точки О:

М₁ = m · C₁ · h₁ = m · C₁ · R₁ cos a₁ .

Подставляя полученные значения М₂ и М₁ в формулу (6.1), получим

DМ = m (C₂ · R₂ · cos a₂ - C₁ · R₁ ·cos a₁).

Или, зная, что секундная масса жидкости равна m = r ·Q, можно записать

DМ = r · Q (C₂ · R₂ ·cos a₂ - C₁ · R₁ ·cos a₁).

Умножим левую и правую часть полученного выражения на угловую скорость W. Тогда произведение момента количества движения на угловую скорость в левой части выражения даст величину теоретической мощности при бесконечном числе лопаток, т.е N_т.¥ =r·g·H_т.¥, а в правой - произведение угловой скорости на радиус даст окружную скорость U. С учетом этого получим

r ·g ·Н_т.¥ = r ·Q (C₂ ·U₂ ·cos a₂ - C₁ ·U₁ cos a₁).

Здесь Н_т.¥-теоретический напор, который способно развить рабочее колесо, имея бесконечное количество лопаток.

Сократив на r·g, получим

Н_т.¥ = (С₂ ·U₂ cosa ₂ - C₁ ·U₁ cos a ₁)/g. (6.2)

Это есть уравнение Эйлера, которое названо основным уравнением работы центробежного насоса.

Для того чтобы иметь как можно больший напор, в выражении (6.2) вычитаемое должно быть равно 0. Это можно получить, если угол a₁ будет равен 90^о. Тогда

Н_т.¥= (С₂ ·U₂ cos a₂) /g. (6.3)

Такая конструкция рабочего колеса применяется во всех отечественных насосах.

Дата добавления: 2015-07-02