Влияние угла загиба лопаток на напор рабочего колеса

На рис.6.2 изображены параллелограммы векторов скоростей на входе в проточный канал и на выходе из него. Ввиду симметричности параллелограмма можно рассматривать его половину в виде треугольника (рис.6.4).

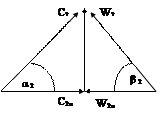Кроме того, ранее были получены формулы (6.4) и (6.6), по которым определяются теоретические напор и расход рабочего колеса. Для того чтобы установить между ними связь, решим оба уравнения совместно. Для этого сделаем следующие преобразования с помощью рис.6.4.

Рис. 6.4. Треугольник векторов

скоростей на выходе из проточного

канала

Обозначим проекцию вектора абсолютной скорости С₂ на U₂ через С_2u, а проекцию вектора относительной скорости W₂ на тот же вектор U₂ через W_2u. Тогда

С _2u = C₂ cos a₂, W_2u = W₂ cos b₂.

В то же время С_2u = U₂ - W_2u.

А теперь запишем вышеупомянутое уравнение (6.4)

Н_т = (s_z ·C₂ ·U₂ cos a₂) / g, в которое внесем полученные выше обозначения, т.е. вместо С₂ cos a₂ введем С_2u.

Н_т = (s_z ·U₂ ·C_2u) / g,

или Н_т = [ s_z ·U₂ (U₂ - W_2u)] / g.

В последнем выражении вынесем U₂ за круглую скобку и получим

Н_т = [ s_z ·U₂² (1 - W_2u / U₂) ] / g. (6.8)

Из треугольника скоростей (рис.6.4) видно, что

tgb₂=V₂/W_2u.

Отсюда W_2u = V₂ / tg b₂. (6.9)

Значение радиальной скорости V₂ выразим из формулы (6.6):

V₂ = Q_т / y ·p ·Д₂· b₂.

С учетом этого формула (6.9) примет вид

W_2u = Q_т / y· p ·Д₂ ·b₂ ·tg b₂ ·U₂.

Подставив полученное выражение в формулу (6.8), получим:

Н_т = [ s_z ·U₂² (1 - Q_т / y· p ·Д₂ ·b₂ ·tg b₂ ·U₂) ] / g.

В полученном выражении величины s_z, U₂, y, p, b_2,, Д₂, g являются постоянными. Поэтому можно обозначить s_z U₂² / g через А, а произведение y· p ·Д₂ ·b₂ ·U₂ - через Б. Тогда

Н_т = А (1 - Q_т / Б tg b₂). (6.10)

Полученное уравнение является линейным и показывает, как изменяется напор в зависимости от изменения расхода и угла b₂ (рис. 6.5).

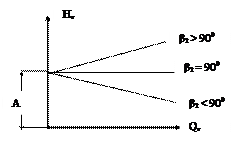Показанная на рис.6.5 связь напора и расхода является ничем иным как теоретической напорной характеристикой насоса с различным углом загиба лопаток рабочего колеса.

Рис. 6.5. Теоретическая связь напора Рис.6.6. Рабочее колесо

и расхода с лопатками, загнутыми против

вращения

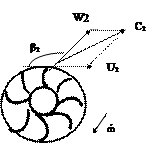
Действительно, если угол b₂>90^о, то tg b₂ < 0, значит, в формуле (6.10) при увеличении Q_т возрастает и Н_т. Рабочее колесо будет иметь вид, показанный на рис. 6.6.

Если угол b₂ = 90^о, то tg b₂ ® ¥, а вычитаемое в формуле (6.10) равно 0. Значит, при любых Q_т значения Н_т не меняются. Рабочее колесо будет иметь вид, показанный на рис.6.7.

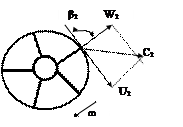Рис.6.7. Рабочее колесо с радиальными

лопатками

В случае, если угол загиба лопаток tgb₂ < 90^o, то он будет положительным, а значит, с увеличением Q_т в формуле (6.10) Н_т будет уменьшаться. Это видно на рис. 6.5. Рабочее колесо будет иметь вид, показанный на рис. 6.8.

Из вышеприведенных рисунков видно, что рабочие колеса с одинаковым диаметром и одной и той же частотой вращения w имеют различную по величине абсолютную скорость на выходе из проточного канала С₂ в зависимости от угла загиба лопаток. Наибольшая скорость при угле b₂ > 90^о. Следовательно жидкость получает здесь наибольшее количество кинетической энергии, которая в насосе должна быть преобразована в потенциальную энергию давления при как можно меньших потерях. Реализовать это на практике очень трудно, и поэтому такие рабочие колеса не применяются. На практике применяются рабочие колеса с углом b₂ в пределах 15...40⁰.

Дата добавления: 2015-07-02