Критерии и формулы подобия центробежных насосов

ПОДОБИЕ И МОДЕЛИРОВАНИЕ ЛОПАСТНЫХ НАСОСОВ

Согласно закону подобия две машины будут подобны, если соблюдаются 3 критерия подобия:

1) геометрическое подобие, т.е. отношение всех геометрических размеров одинаково;

2) кинематическое подобие предполагает,что безразмерные поля скоростей будут подобны, т.е. подобны треугольники скоростей на входе и выходе;

3) динамическое подобие требует, чтобы отношение сил инерции к силам трения или тяжести были бы одинаковыми, т.е. должно соблюдаться равенство отвлеченных параметров Re (число Рейнольдса), Fr (число Фруда), Еи (число Эйлера) или должно быть равным отношение расходов, напоров и мощностей.

Пусть мы имеем два насоса: один маленький (модельный), второй большой (натурный). Согласно первому критерию подобия должно быть

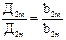(7.1)

где Д_2м и Д_2н – диаметры рабочих колес модельного и натурного насосов, а b_2м и b_2н – ширина их проточной части.

Согласно 2-му критерию подобия треугольники скоростей двух подобных насосов должны быть подобны треугольникам векторов скоростей на выходе из проточного канала натурного и модельного насосов (рис.7.1).

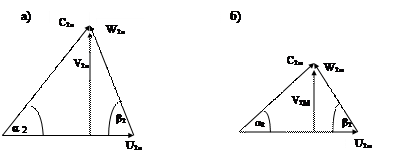
Рис.7.1. Векторные треугольники скоростей на выходе из насосов:

а) натурного, б) модельного

Из подобия треугольников векторов скоростей натурного (а) и модельного (б) насосов (рис.7.1), следует:

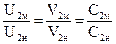(7.2)

Из теоретической механики известно, что окружная (линейная) скорость определяется по формуле U = p Д n / 60. Поэтому формулу (7.1) можно записать так:

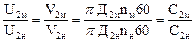(7.3)

Ранее были получены формулы для определения теоретических расхода (6.6) и напора (6.4) рабочего колеса центробежного насоса. Эти формулы применимы и для модельного колеса (Q_м и Н_м), и для натурного (Q_н и Н_н). Запишем отношение расходов и напоров обеих насосов:

;

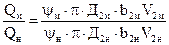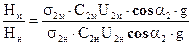
В соответствии с третьим критерием подобия

y_м = y_н ; s_zм = s_zн.

Проведя сокращения равных величин и применив 1-й и 2-й критерии подобия (отношения 7.1, 7.2 и 7.3), получим:

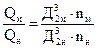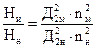(7.4) (7.5)

Формула (7.4) - первая формула подобия, (7.5) - вторая формула подобия. Для получения третьей формулы подобия запишем отношение мощностей модельного и натурного насосов, которые определяются по общей формуле

N = 9, 81 Q Н.

Тогда

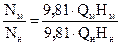
Или, подставив в полученное выражение формулы (7.4) и (7.5) и сократив, получим третью формулу подобия

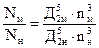(7.6)

Если рассматривать один и тот же насос, у которого может меняться только частота вращения рабочего колеса, то можно записать:

Д_2м = Д_2н; n_м = n₁; n_н = n₂. Тогда формулы (7.4), (7.5) и (7.6) примут вид:

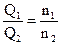(7.7); 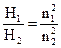(7.8); 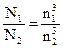(7.9).

Полученные выражения называются формулами пропорциональности, позволяющие пересчитывать основные параметры насоса на другую частоту вращения рабочего колеса.

Дата добавления: 2015-07-02