
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нерезкое маскирование и фильтрация с подъемом высоких частот
|
|
|
|
Процедура, много лет использующаяся в полиграфии для повышения резкости изображений, заключается в вычитании из изображения его расфокусированной копии. Эта процедура, называемая нерезким маскированием, выражается формулой
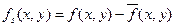 (14)
(14)
Где  обозначает изображение с повышенной резкостью, полученное нерезким маскированием, a
обозначает изображение с повышенной резкостью, полученное нерезким маскированием, a  - расфокусированная копия исходного изображения
- расфокусированная копия исходного изображения  . Нерезкое маскирование ведет свое начало из фотографии, где для получения более резкого отпечатка на негатив накладывался расфокусированный позитив, и экспозиция осуществлялась через полученный двухслойный оригинал.
. Нерезкое маскирование ведет свое начало из фотографии, где для получения более резкого отпечатка на негатив накладывался расфокусированный позитив, и экспозиция осуществлялась через полученный двухслойный оригинал.
Некоторым обобщением нерезкого маскирования является фильтрация с подъемом высоких частот. Процедура фильтрации с подъемом высоких частот, формирующая изображение 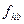 , задается формулой:
, задается формулой:
 (15)
(15)
где 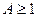 , а
, а  , как и раньше, расфокусированная копия f. Это уравнение может быть записано в виде:
, как и раньше, расфокусированная копия f. Это уравнение может быть записано в виде:
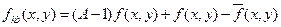 (16)
(16)
Используя уравнение (14), получим:
fhb(x,y) = (A-1)f(x,y)+fs(x,y) (17)
как формулу для вычисления результата фильтрации изображения с подъемом высоких частот.
Уравнения (15) и (17), вообще говоря, не определяют жестко способ получения резкого изображения. Можно выбрать использование лапласиана, тогда fs(x, у) может быть получено из уравнения (13). В этом случае уравнение (17) будет иметь вид:
 (18)
(18)
Здесь, как и ранее, w(0,0) есть значение центрального коэффициента маски лапласиана. Фильтрация с подъемом высоких частот также может быть реализована за один проход при использовании одной из масок, показанных на Рис.9. Заметим, что при А = 1 фильтрация с подъемом высоких частот становится «стандартным» повышением резкости с помощью лапласиана. При увеличении А больше 1, эффект увеличения резкости становится все меньше и меньше. В конце концов, при достаточно больших А, результат фильтрации изображения с подъемом высоких частот будет приблизительно совпадать с результатом умножения исходного изображения на константу.
Пример: Улучшение изображения при помощи фильтра, усиливающего высокие частоты
Одним из типичных приложений фильтрации изображения с подъемом высоких частот является случай, когда исходное изображение темнее, чем это требуется. Варьированием коэффициента усиления высоких частот обычно удается добиться общего увеличения яркости изображения и получить желаемый результат.


а б


в г
Рис. 8 (а) То же изображение, что и на Рис.7 (в), но более темное;
(б) Лапласиан изображения (а), полученный при использовании маски Рис.7 (б) с А=0; (в) Изображеие, улучшенное наложением лапласиана с маской Рис.7 (б) и А=1; (г) То же, что и (в), но с А=1.7
На рисунке показано изображение-лапласиан, полученное при использовании маски (Рис.9 б) с А= 0. Изображение на Рис.8 (в) было получено при той же маске, но с А = 1. Как и ожидалось, изображение стало более резким, но все еще остается столь же темным, что и исходное. Наконец, на Рис.8(г) показан результат при А = 1,7. Этот результат намного более приемлем, поскольку увеличен средний уровень яркости, а следовательно изображение стало более светлым и естественным. ■


а б
Рис. 9 Метод фильтрации изображения с подъемом высоких частот
6. Улучшение изображений с использованием первых производных: градиент
Вобработке изображений первые производные реализуются через модуль градиента. Для функции f(х, у) градиент в точке (х, у) определяется как двумерный вектор-столбец:
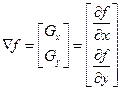 (19)
(19)
Модуль этого вектора определяется следующим образом:
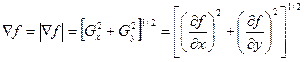
(20)
Компоненты вектора градиента являются линейными операторами, но модуль вектора, очевидно, нет, поскольку он выражается через операции возведения в квадрат и извлечения квадратного корня. С другой стороны, частные производные в уравнении (19) не являются инвариантными к повороту (изотропными), но модуль вектора градиента таковым является. Хотя это и не является строго правильным, модуль вектора градиента часто называют градиентом.
Объем вычислений, необходимый для обработки всего изображения оператором (20), достаточно велик, поэтому частой практикой является приближение значения модуля градиента суммой модулей отдельных компонентов, вместо квадратов и квадратных корней:
 (21)
(21)
Это уравнение проще в вычислениях, оно все еще сохраняет относительные изменения в уровнях яркостей, но свойство изотропности пропадает. Однако, как и в случае лапласиана, свойства изотропности для определяемого в следующем абзаце дискретного градиента сохраняются только для ограниченного набора угловых приращений, который зависит от масок, используемых для приближения производных. Как оказывается, маски, наиболее часто используемые для приближения градиента, дают те же результаты только для углов, кратных 90°. Эти результаты не зависят от того, какое уравнение используется - (20) или (21), так что при использовании более простого уравнения (21) ничего существенного не теряется.
Аналогично лапласиану, первоначально будут определены дискретные приближения приведенных выше уравнений, а затем уже по ним будут сформированы соответствующие маски фильтров. Чтобы упростить последующие рассуждения, для указания точек в окрестности 3x3 будут использоваться обозначения, показанные на Рис.10. Так, например, центральная точка z5 обозначает f(x, у), z1обозначает f(x-1, у-1), и так далее.


б в
а

г д
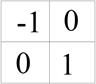
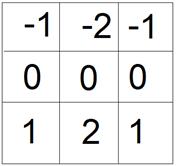
Рис. 10 Область изображения размерами 3х3 элемента (z1…z9 – значения яркости соответствующих пикселей под маской) и маски, используемые для вычисления градиента в точке, отмеченной z5. Суммы коэффициентов по каждой из масок равны нулю.
Простейшими приближениями первой производной, являются следующие:
Gx = (Z8 — Z5) и Gy = (Z6 - Z5).
Два других определения, предложенные Робертсом в ранних исследованиях по цифровой обработке изображений, используют перекрестные направления:
Gx=(Z9 – Z5) и Gy=(Z8 – Z6). (22)
Если выбрать уравнение (20), то градиент будет вычисляться по следующей формуле:
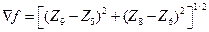 (23)
(23)
Если используются абсолютные значения, тогда, подставляя уравнения (22) в (21), получим следующее приближение к значениям градиента:
 (24)
(24)
Это уравнение может быть реализовано с помощью двух масок Рис.10 (б) и (в). Эти маски называют перекрестным градиентным оператором Робертса. Однако маски четного размера реализовывать неудобно. Наименьшая маска фильтра, которая нас интересует, имеет размеры 3x3. Приближением, использующим абсолютные значения для той же самой точки Z5, но уже по маске 3x3, будет:
 (25)
(25)
Разность между значениями пикселей в третьей и первой строках окрестности 3x3 приближает значение производной по направлению х, а разность между значениями пикселей в третьем и первом столбцах приближает значение производной по направлению у. Маски Рис.10 (г) и (д), называют оператором Собеля (Sobel). Они могут использоваться для реализации уравнения (25). Заметим, что суммы коэффициентов каждой из масок равны 0, и это означает, что на участках изображения с постоянным уровнем яркости отклик любого из приведенных операторов будет равен 0, как и должно быть у оператора, соответствующего первой производной.
Пример: Применение градиента для улучшения контуров


|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 1886; Нарушение авторских прав?; Мы поможем в написании вашей работы!