Интегральный признак Коши 2 страница

Вывод: Исследуемый ряд сходится абсолютно.

Правда, при втором способе решения есть риск, что преподаватель оценит хитро… смекалку студента и забракует задание. А может и не забракует.

И напоследок пара примеров для самостоятельного решения. Один из той же оперы (перечитайте справку), но попроще. Другой для гурманов – на закрепление интегрального признака сходимости.

Пример 9

Исследовать ряд на сходимость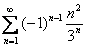

Пример 10

Исследовать ряд на сходимость

После качественной проработки числовых положительных и знакопеременных рядов с чистой совестью можно перейти к функциональным рядам, которые не менее монотонны и однообразны интересны.

Желаю успехов!

Решения и ответы:

Пример 4: Используем признак Лейбница:

1)
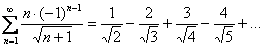
Данный ряд является знакочередующимся.
2)

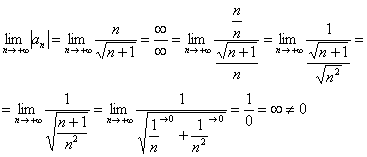
Члены ряда не убывают по модулю.
Вывод: Ряд расходится.
Примечание: В данном примере неопределенность устраняется стандартным способом: делением числителя и знаменателя на «эн» в старшей степени. Старшая степень числителя: 1, старшая степень знаменателя: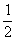

Пример 5: Используем признак Лейбница.
1)
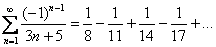
Ряд является знакочередующимся.
2) – члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше, чем предыдущий: 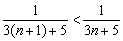, значит, убывание монотонно.
Ряд сходится по признаку Лейбница.
Исследуем ряд на абсолютную сходимость:

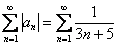
Сравним данный ряд с расходящимся гармоническим рядом 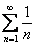. Используем предельный признак сравнения:
– конечное число, отличное от нуля, значит, ряд 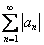расходится вместе с гармоническим рядом.
Исследуемый ряд сходится только условно.

Пример 7: Используем признак Лейбница.
1)
Ряд является знакочередующимся.
2) – члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше, чем предыдущий, значит, убывание монотонно.
Ряд сходится по признаку Лейбница.
Исследуем ряд на абсолютную сходимость:

Используем признак Даламбера:

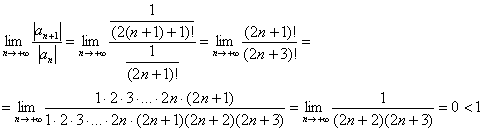
Таким образом, ряд 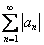сходится.
Исследуемый ряд сходится абсолютно.

Примечание: Возможно, не всем понятно, как разложены факториалы. Это всегда можно установить опытным путём, возьмём и сравним какие-нибудь соседние члены ряда:
и , следующий член ряда к предыдущему:
и , следующий член ряда к предыдущему: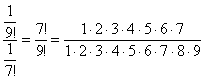
…

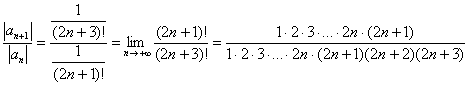
Пример 9: Используем признак Лейбница.
1)
Ряд является знакочередующимся.
2) – так как 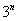более высокого порядка роста, чем
Члены ряда убывают по модулю, начиная с некоторого номера 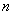, при этом, каждый следующий член ряда по модулю меньше, чем предыдущий, таким образом, убывание монотонно.
Вывод: Ряд сходится.
Исследуем ряд на абсолютную сходимость:

Используем признак Даламбера:

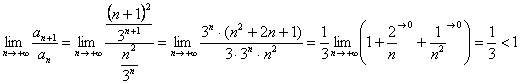
Таким образом, ряд 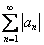– сходится.
Исследуемый ряд сходится абсолютно.

Пример 10: Используем признак Лейбница.
1)
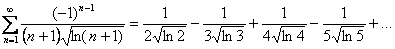
Ряд является знакочередующимся.
2) – члены ряда убывают по модулю. Каждый следующий член ряда по модулю меньше, чем предыдущий, значит, убывание монотонно.
Ряд сходится по признаку Лейбница.
Исследуем ряд на абсолютную сходимость:

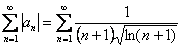
Используем интегральный признак.

Подынтегральная функция непрерывна на .

Таким образом, ряд 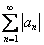расходится вместе с соответствующим несобственным интегралом.

Исследуемый ряд сходится только условно.

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Числовые ряды повышенной сложности

Не ходите, дети, в Африку гулять

Битый час мучаетесь со сходимостью числового ряда? Упорно не работают признаки сравнения, признаки Даламбера и Коши? Сто долларов в зачётку. В такой ситуации неоднократно оказывается практически каждый студент… сложная производная, сложный интеграл, сложная задача по геометрии и вот теперь очередь дошла до неприступного числового ряда. Причём, злись не злись, психуй не психуй, а покорить его надо.

Насколько часто такие ряды попадаются на практике? По моей субъективной оценке, их объём составляет где-то 10-15% от общего количества задач типовой работы по теме (если у вас заметно больше – Ряды для чайников). Таким образом, вероятность приятной встречи очень велика, и данная статья как раз рассчитана на тех читателей, которые уже достаточно уверенно умеют исследовать сходимость числового ряда 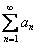стандартными методами, но зашли в тупик с очередным примером.

В чём состоит трудность и где может быть загвоздка? Отложим в сторону намыленную верёвку, спокойно проанализируем причины и ознакомимся с практическими приёмами решения.

Первое, и самое главное: в подавляющем большинстве случаев для исследования сходимости ряда необходимо применить какой-нибудь знакомый способ, но общий член ряда 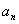набит настолько хитрой начинкой, что совершенно не очевидно, что с ней делать. И вы ходите по кругу: не срабатывает первый признак, не годится второй, не получается третьим, четвёртым, пятым методом, потом черновики отбрасываются в сторону и всё начинается заново. Обычно это связано с недостатком опыта или пробелами в других разделах математического анализа. В частности, если запущены пределы последовательностей и поверхностно разобраны пределы функций, то придётся туго.

Иными словами, человек просто не видит нужный приём решения в силу недостатка знаний или опыта.

Бывает виновато и «затмение», когда, например, элементарно не выполнен необходимый признак сходимости ряда, но по незнанию, невнимательности либо небрежности это выпадает из поля зрения. И получается как в той байке, где профессор математики решил детскую задачку с помощью диких рекуррентных последовательностей и числовых рядов =)

В лучших традициях сразу живые примеры: ряды и их родственники – расходятся, так как в теории доказаны пределы последовательностей 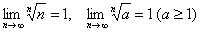. Скорее всего, в первом семестре из вас вытрясут душу за доказательство на 1-2-3 страницы, но сейчас вполне достаточно показать невыполнение необходимого условия сходимости ряда, сославшись на известные факты. Известные? Если студент не знает, что корень энной степени – штука чрезвычайно мощная, то, скажем, ряды 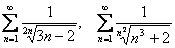поставят его в тупик. Хотя решение, как дважды два: , т.е. по понятной причине оба ряда расходятся. Скромного комментария «данные пределы доказаны в теории» (или даже вовсе его отсутствия) вполне хватит для зачёта, всё-таки выкладки достаточно тяжёлые и относятся они точно не к разделу числовых рядов.

А изучив ближайшие примеры, вы будете только удивляться краткости и прозрачности многих решений:

Пример 1

Исследовать сходимость ряда

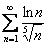
Решение: прежде всего, проверяем необходимый признак сходимости ряда. Это не формальность, а отличный шанс расправиться с примером «малой кровью».

Числовая последовательность более высокого порядка роста, чем , поэтому , то есть необходимый признак сходимости выполнен, и ряд может, как сходиться, так и расходиться. Ну что же, попытка – не пытка. Следует отметить, что для чайников тот же предел вовсе не очевиден, поэтому по ходу дела я ненавязчиво расставляю ссылки;-)

Таким образом, нужно использовать какой-либо признак. Но какой? Предельный признак сравнения явно не подходит, поскольку в общий член ряда затесался логарифм, признаки Даламбера и Коши тоже не приводят к результату. Если бы у нас был , то худо-бедно можно было бы вывернуться через интегральный признак.

«Осмотр места происшествия» наводит на мысль о расходящемся ряде (случай обобщенного гармонического ряда), но опять же возникает вопрос, как учесть логарифм в числителе?

Остаётся самый первый признак сравнения, основанный на неравенствах, который часто не принимается во внимание и пылится на дальней полке. Распишем ряд подробнее:

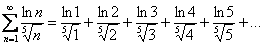
Напоминаю, что – неограниченно растущая числовая последовательность:

И, начиная с номера 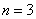, будет выполнено неравенство :

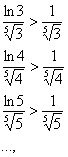
то есть, члены ряда 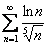будут ещё больше соответствующих членов расходящегося ряда .

В итоге, ряду 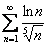ничего не остаётся, как тоже расходиться.

Здесь я невзначай использовал простое утверждение математического анализа: сходимость или расходимость числового ряда зависит от его «бесконечного хвоста» (остатка). В нашем случае мы можем не принимать во внимание тот факт, что неравенство неверно для первых двух номеров – это не оказывает влияния на сделанный вывод.

Чистовое оформление примера должно выглядеть примерно так:

“
Сравним данный ряд с расходящимся рядом .
Для всех номеров, начиная с 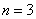, выполнено неравенство , следовательно, по признаку сравнения исследуемый ряд расходится.
“

Три строчки. Всё!

Естественно, такому лаконичному оформлению предшествует мысленный анализ либо разбор полётов на черновике. Само собой не возбраняется расписать решение и подробно, но почти всегда идёт «на ура» и короткая версия.

Пример 2

Исследовать сходимость ряда

Это пример для самостоятельного решения. Подумайте, подберите ряд для сравнения, распишите ряды. Вот вам и истинный математический анализ =) Примерный образец оформления в конце урока.

С увлечением рассматриваем в бинокль других дикобразов:

Пример 3

Исследовать сходимость ряда

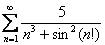
Решение: константа-множитель общего члена не влияет на сходимость или расходимость ряда, поэтому выносим её за пределы суммы:

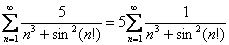
Напрашивается сравнение с рядом 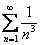, и предчувствие не обманывает. Всего-то лишь немного проанализировать чудо в перьях:

Последовательность 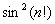– ограничена:

Следовательно, для любых натуральных номеров справедливо следующее неравенство:

А дробь с бОльшим знаменателем будет меньше дроби с мЕньшим знаменателем:
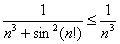– для всех «эн» (кто не врубился во фразу – условный пример: ).

То есть, члены ряда 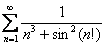ещё меньше соответствующих членов сходящегося ряда 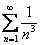, и нашему ряду тоже ничего не остаётся, как сходиться.

Вывод: по признаку сравнения исследуемый ряд сходится.

Если что-то показалось мутным или не очень понятным, рекомендую расписать члены обоих рядов (на худой конец приблизительно вычислить их на калькуляторе), сравнить между собой и снова перечитать выкладки.

Второй способ решения: в данном примере годится и предельный признак сравнения. Сравним исследуемый ряд со сходящимся рядом :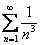

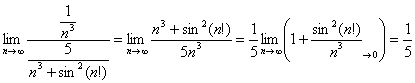
Обратите внимание, что с выносом «пятёрки» тут можно не возиться и отношение общих членов выгоднее составить именно так, а не наоборот: 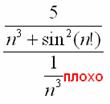. На завершающем этапе использована теорема: произведение бесконечно малой последовательности на ограниченную последовательность – есть бесконечно малая последовательность (см. урок о числовых последовательностях). В нашем случае последовательность – бесконечно малА, а 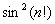– ограничена, следовательно, .

Вывод: в пределе получено конечное число, отличное от нуля, значит, исследуемый ряд сходится вместе с рядом .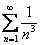

Но предельный признак сравнения работает далеко не всегда. Пара коротких заданий для самостоятельного решения:

Пример 4

Исследовать сходимость ряда

Многие читатели уже видят, с чем нужно сравнивать, и что ряд явно расходится. Здесь не пригоден признак сравнения с неравенствами, поскольку 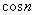принимает как положительные, так и отрицательные значения, а значит, условие справедливо далеко не всегда.

Пример 5

Исследовать сходимость ряда

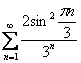
Здесь же ситуация обратная – не работает предельный признак сравнения.

Примерные образцы оформления задач в конце урока.

Не редкость, когда приходится проводить двухходовое (а то и трёхходовое) рассуждение:

Пример 6

Исследовать сходимость ряда

Решение: сначала аккуратно разбираемся с тарабарщиной числителя. Последовательность 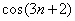– ограничена: 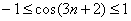. Тогда:

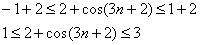
Сравним наш ряд с рядом 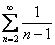. В силу только что полученного двойного неравенства, для всех «эн» будет выполнено:

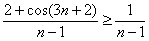
Теперь сравним ряд 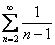с расходящимся гармоническим рядом .

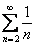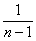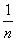
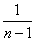Знаменатель дроби меньше знаменателя дроби , поэтому сама дробь – больше дроби 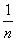(распишите несколько первых членов, если не понятно). Таким образом, для любого «эн»:

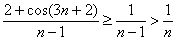
А значит, по признаку сравнения ряд расходится вместе с гармоническим рядом.

Если немного видоизменить знаменатель: , то первая часть рассуждений будет аналогична: 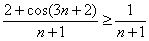. Но вот для доказательства расходимости ряда уже применим только предельный признак сравнения, так как неравенство 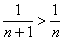неверно.

Ситуация со сходящимися рядами «зеркальна», то есть, например, для ряда можно использовать оба признака сравнения (неравенство 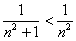справедливо), а для ряда 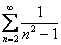– только предельный признак (неравенство 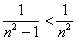неверно).

Продолжаем наше сафари по дикой природе, где на горизонте замаячило стадо грациозных и сочных антилоп:

Пример 7

Исследовать сходимость ряда

Решение: необходимый признак сходимости выполняется, и мы снова задаёмся классическим вопросом: что делать? Перед нами нечто напоминающее сходящийся ряд , однако, чёткого правила тут нет – такие ассоциации зачастую обманчивы.

Зачастую, да не в этот раз. С помощью предельного признака сравнения сравним наш ряд со сходящимся рядом . В ходе вычисления предела используем замечательный предел , где в качестве бесконечно малой величины выступает :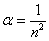

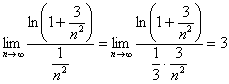
Получено конечное число, отличное от нуля, значит, исследуемый ряд сходится вместе с рядом .

Вместо применения стандартного искусственного приёма домножения и деления на «тройку», можно было изначально провести сравнение со сходящимся рядом .
Но здесь желательна оговорка, что константа-множитель общего члена не влияет на сходимость ряда. И как раз в таком стиле оформлено решение следующего примера:

Пример 8

Исследовать сходимость ряда

Образец в конце урока.

Где замечательные пределы, там неподалёку и замечательные эквивалентности:

Пример 9

Исследовать сходимость ряда

Решение: в предыдущих примерах мы пользовались ограниченностью синуса, но сейчас это свойство оказывается вне игры. Знаменатель дроби, более высокого порядка роста, чем числитель, поэтому при 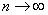аргумент синуса и весь общий член бесконечно малЫ. Необходимое условие сходимости, как понимаете, выполнено, что не позволяет нам отлынивать от работы.

Проведём разведку: в соответствии с замечательной эквивалентностью , мысленно отбросим синус и получим ряд 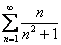. Ну а уж такое-то….

Оформляем решение:

Сравним исследуемый ряд с расходящимся рядом 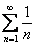. Используем предельный признак сравнения:

Заменим бесконечно малую эквивалентно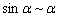й: при .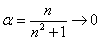

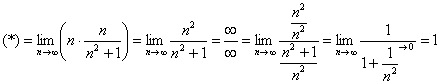
Получено конечное число, отличное от нуля, значит, исследуемый ряд расходится вместе с гармоническим рядом.

Готово.

Пример 10

Исследовать сходимость ряда

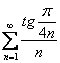
Это пример для самостоятельного решения.

Для планирования дальнейших действий в подобных примерах здОрово помогает мысленное отбрасывание синуса, арксинуса, тангенса, арктангенса. Но помните, такая возможность существует лишь при бесконечно малом аргументе, не так давно мне попался провокационный ряд:

Пример 11

Исследовать сходимость ряда
.

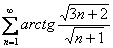Решение: здесь бесполезно использовать ограниченность арктангенса, и эквивалентность 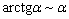тоже не работает. Выход неожиданно прост:

Исследуемый ряд расходится, так как не выполнен необходимый признак сходимости ряда.

Вторая причина «затыка на задании» состоит в приличной навороченности общего члена 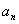, что вызывает затруднения уже технического характера. Грубо говоря, если рассмотренные выше ряды относятся к разряду «хрен догадаешься», то эти – к категории «хрен решишь». Собственно, это и называют сложностью в «обычном» понимании. Далеко не каждый правильно разрулит несколько факториалов, степеней, корней и прочих обитателей саванны. Больше всего проблем доставляют, конечно же, факториалы:

Пример 12

Исследовать сходимость ряда

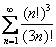
Решение: очевидно, что нужно использовать признак Даламбера. Но ошибку проще простого допустить при разложении факториалов. Что такое факториал и как его расписать, подробно разобрано в статьях Пределы числовых последовательностей и Признак Даламбера, признаки Коши.

Как возвести факториал в степень? Легко. По правилу действий со степенями, необходимо возвести в степень каждый множитель произведения:

И, конечно же, внимание и ещё раз внимание, сам-то по себе признак Даламбера работает традиционно:

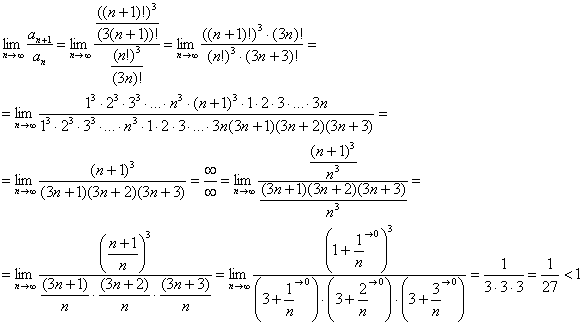
Таким образом, исследуемый ряд сходится.

Сфотографируйте рациональную методику устранения неопределённости : когда понятен порядок роста числителя и знаменателя – совсем не обязательно мучаться и раскрывать скобки.

Пример 13

Исследовать сходимость ряда

Дата добавления: 2015-07-02