Интегральный признак Коши 3 страница

Зверь очень редкий, но встречается, и было бы несправедливым обойти его объективом камеры.

Что такое факториал с двойным восклицательным знаком? Факториал 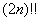«накручивает» произведение чётных чисел:

И, на всякий случай, для справки: факториал 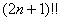«накручивает» произведение нечётных чисел:

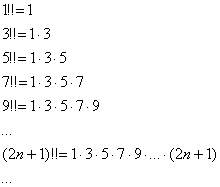
Проанализируйте, в чём состоит отличие от 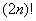и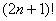

Пример 14

Исследовать сходимость ряда

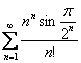
А в этом задании постарайтесь не запутаться со степенями, замечательными эквивалентностями и замечательными пределами.

Образцы решений и ответы в конце урока.

Но студент достаётся на корм не только тиграм – свою добычу выслеживают и хитрые леопарды:

Пример 15

Исследовать сходимость ряда

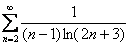
Решение: практически мгновенно отпадают необходимый признак сходимости, предельный признак, признаки Даламбера и Коши. Но хуже всего, что бессилен неоднократно выручавший нас признак с неравенствами. Действительно, сравнение с расходящимся рядом 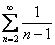невозможно, так как неравенство 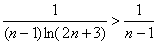неверно – множитель-логарифм только увеличивает знаменатель, уменьшая саму дробь 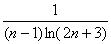по отношению к дроби 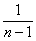. И другой глобальный вопрос: а почему мы вообще изначально уверены, что наш ряд 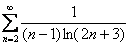непременно обязан расходиться и его нужно сравнивать с каким-либо расходящимся рядом? Вдруг он вообще сходится?

Интегральный признак? Несобственный интеграл 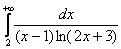навевает траурное настроение. Вот если бы у нас был ряд 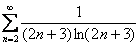… тогда да. Стоп! Так и рождаются идеи. Оформляем решение в два шага:

1) Сначала исследуем сходимость ряда 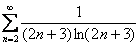. Используем интегральный признак:

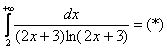
Подынтегральная функция непрерывна на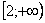

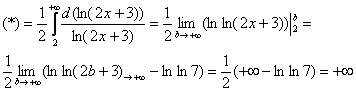
Таким образом, ряд 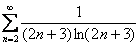расходится вместе с соответствующим несобственным интегралом.

2) Сравним наш ряд с расходящимся рядом 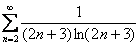. Используем предельный признак сравнения:

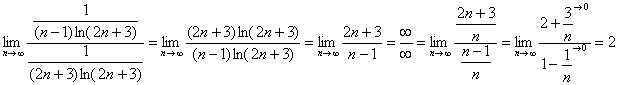
Получено конечное число, отличное от нуля, значит, исследуемый ряд расходится вместе с рядом .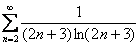

И в таком решении нет ничего необычного или творческого – так и надо решать!

Предлагаю самостоятельно оформить следующую двухходовку:

Пример 16

Исследовать сходимость ряда

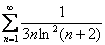
Студент с некоторым опытом в большинстве случаев сразу видит, сходится ряд или расходится, но, бывает, что хищник ловко маскируется в кустах:

Пример 17

Исследовать сходимость ряда

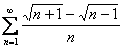
Решение: на первый взгляд вообще не понятно, как ведёт себя этот ряд. А если перед нами туман, то логично начать с черновой проверки необходимого условия сходимости ряда. В целях устранения неопределённости используем непотопляемый метод умножения и деления на сопряженное выражение:

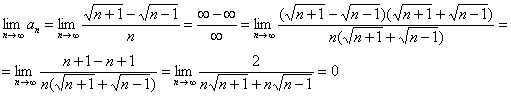
Необходимый признак сходимости не сработал, но вывел на чистую воду нашего тамбовского товарища. В результате выполненных преобразований получен эквивалентный ряд 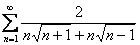, который в свою очередь сильно напоминает сходящийся ряд .

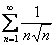Записываем чистовое решение:

Сравним данный ряд со сходящимся рядом 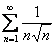. Используем предельный признак сравнения:

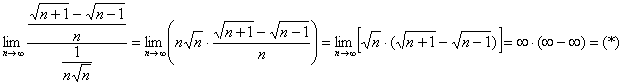
Умножим и разделим на сопряженное выражение:

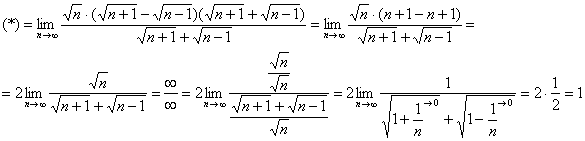
Получено конечное число, отличное от нуля, значит, исследуемый ряд сходится вместе с рядом .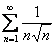

Возможно, у некоторых возник вопрос, откуда на нашем африканском сафари появились волки? Не знаю. Завезли, наверное. Следующую трофейную шкуру добывать вам:

Пример 18

Исследовать сходимость ряда

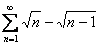
Примерный образец решения в конце урока

И, наконец, ещё одна мысль, которая в отчаянии посещает многих студентов: а не использовать ли более редкий признак сходимости ряда? Признак Раабе, признак Абеля, признак Гаусса, признак Дирихле и прочие неведомые зверушки. Идея рабочая, но в реальных примерах осуществляется очень редко. Лично я за все годы практики лишь 2-3 раза прибегнул к признаку Раабе, когда действительно ничего не помогло из стандартного арсенала. Полностью воспроизвожу ход своего экстремального квеста:

Пример 19

Исследовать сходимость ряда

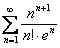
Решение: Безо всяких сомнений признак Даламбера. В ходе вычислений активно использую свойства степеней, а также второй замечательный предел:

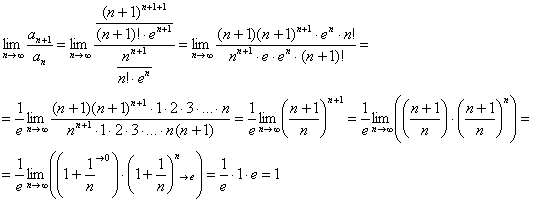
Вот тебе и раз. Признак Даламбера не дал ответа, хотя ничего не предвещало такого исхода.

Пошерстив справочник, я нашёл доказанный в теории малоизвестный предел 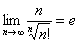и применил более сильный радикальный признак Коши:

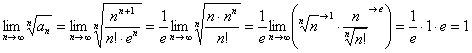
Вот тебе и два. И, главное, совершенно не понятно, сходится ряд 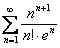или расходится (крайне редкая для меня ситуация). Необходимый признак сравнения? Без особых надежд – даже если немыслимым образом разберусь с порядком роста числителя и знаменателя, то это ещё не гарантирует вознаграждения.

Полный даламбер, но самое скверное, что ряд нужно решить. Нужно. Ведь это будет первый случай, когда я сдамся. И тут мне вспомнилось, что вроде существуют ещё какие-то более сильные признаки. Передо мной был уже не волк, не леопард и не тигр. Это был огромный слон, размахивающий большим хоботом. Пришлось взять в руки гранатомёт:

Дата добавления: 2015-07-02