Признак Раабе

Рассмотрим положительный числовой ряд .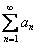
Если существует предел 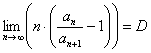, то:
а) При ряд расходится. Причём полученное значение может быть нулевым или отрицательным
б) При 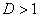ряд сходится. В частности, ряд сходится при .
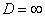в) При 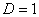признак Раабе не даёт ответа.

Составляем предел и бережно-аккуратно упрощаем дробь:

Да, картина, мягко говоря, неприятная, но я уже не удивился.Подобные пределы раскалываются с помощью правила Лопиталя, и первая мысль, как потом выяснилась, оказалось правильной. Но сначала я где-то час я крутил-вертел предел «обычными» методами, однако неопределённость 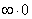не желала устраняться. А ходьба по кругу, как подсказывает опыт – типичный признак того, что выбран неверный способ решения.

Пришлось обратиться к русской народной мудрости: «Если ничего не помогает, прочитайте инструкцию». И когда я открыл 2-ой том Фихтенгольца, то к великой радости обнаружил исследование идентичного ряда . И дальше пошло решение по образцу:

Поскольку числовая последовательность считается частным случаем функции, то в пределе 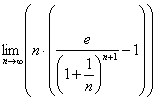проведём замену: 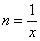. Если 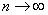, то .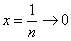

В результате:

Теперь у меня предел функции и применимо правило Лопиталя. В процессе дифференцирования придётся брать производную степенно-показательной функции, которую технически удобно найти отдельно от основного решения:

ТерпИте, раз уж сюда забрались – Бармалей в начале статьи предупреждал =) =)

Дважды использую правило Лопиталя:

Таким образом, исследуемый ряд расходится.

Потрачена уйма времени, но мои ворота устояли!

Ради интереса я вычислил 142 члена ряда в Экселе (на бОльшее не хватило вычислительной мощности) и похоже (но строго теоретически не гарантировано!), что для данного ряда не выполнен даже необходимый признак сходимости. Посмотреть эпический результат можно здесь >>> После таких злоключений не удержался от соблазна этим же любительским способом проверить и предел .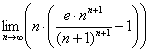

Пользуйтесь на здоровье, решение легально!

А это ваш слонёнок:

Пример 20

Исследовать сходимость ряда

Если вы хорошо прониклись идеями данного урока, то справитесь с этим примером! Он значительно проще предыдущего;-)

Наше путешествие завершилось на яркой ноте, и, надеюсь, у всех оставило незабываемое впечатление. Желающие продолжения банкета могут пройти на страницу Готовые задачи по высшей математике и закачать архив с дополнительными заданиями по теме.

Желаю успехов!

Решения и ответы:

Пример 2: Решение: сравним данный ряд со сходящимся рядом . Для всех натуральных номеров справедливо неравенство , а значит, по признаку сравнения исследуемый ряд сходится вместе с рядом .

Пример 4: Решение: сравним данный ряд с расходящимся гармоническим рядом. Используем предельный признак сравнения:

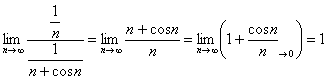
(произведение бесконечно малой 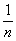на ограниченную 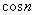– есть бесконечно малая последовательность)
Получено конечное число, отличное от нуля, значит, исследуемый ряд расходится вместе с гармоническим рядом.

Пример 5: Решение: вынесем множитель-константу общего члена за пределы суммы, от него не зависит сходимость или расходимость ряда:

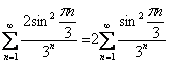
Сравним данный ряд со сходящейся бесконечно убывающей геометрической прогрессией 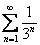. Последовательность 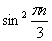– ограничена: 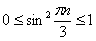, поэтому для всех натуральных номеров выполнено неравенство 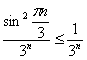. А, значит, по признаку сравнения исследуемый ряд сходится вместе с рядом .

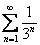Пример 8: Решение: сравним данный ряд с расходящимся рядом 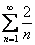(константа-множитель общего члена не влияет на сходимость или расходимость ряда). Используем предельный признак сравнения и замечательный предел :

Получено конечное число, отличное от нуля, значит, исследуемый ряд расходится вместе с рядом .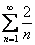

Пример 13: Решение: используем признак Даламбера:

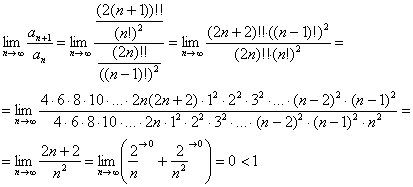
Таким образом, исследуемый ряд сходится.

Пример 14: Решение: используем признак Даламбера:

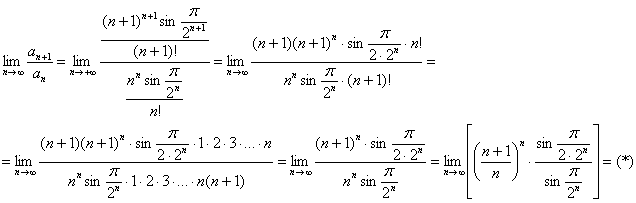
Заменим бесконечно малые эквивалентным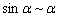и: при .
Используем второй замечательный предел: .

Следовательно, исследуемый ряд расходится.

Пример 16: Решение:
1) Исследуем сходимость ряда 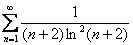. Используем интегральный признак:

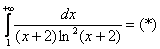
Подынтегральная функция непрерывна на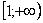

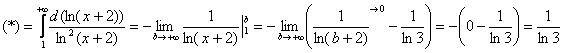
Получено конечное число, значит, ряд 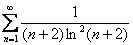сходится.
2) Сравним исследуемый ряд со сходящимся рядом 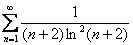. Для всех номеров выполнено неравенство , следовательно, по признаку сравнения исследуемый ряд сходится.

Пример 18: Решение: сравним данный ряд с расходящимся рядом . Используем предельный признак сравнения:

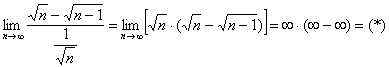
Умножим и разделим на сопряженное выражение:

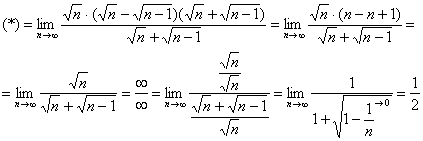
Получено конечное число, отличное от нуля, значит, исследуемый ряд расходится вместе с рядом .

Пример 20: Решение: проверим необходимое условие сходимости ряда. В ходе вычислений типовым приёмом организуем 2-ой замечательный предел:

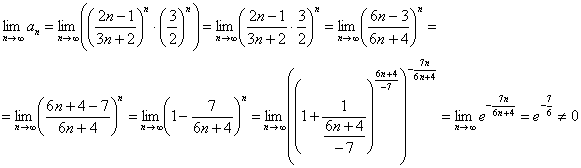
Таким образом, исследуемый ряд расходится.

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Дата добавления: 2015-07-02