Преобразование Уолша и его применение для обработки сигналов

Функциями Уолша называется семейство функций, образующих ортогональную систему, принимающих значения только 1 и −1 на всей области определения.

В принципе, функции Уолша могут быть представлены в непрерывной форме, но чаще их определяют как дискретные последовательности из элементов. Группа из функций Уолша образует матрицу Адамара.

Функции Уолша получили широкое распространение в радиосвязи, где с их помощью осуществляется кодовое разделение каналов (CDMA), например, в таких стандартах сотовой связи, как IS-95, CDMA2000 или UMTS.

Система функций Уолша является ортонормированным базисом и, как следствие, позволяет раскладывать сигналы произвольной формы в обобщённый ряд Фурье.

Преобразование Уолша-Адамара

Является частным случаем обобщённого преобразования Фурье, в котором базисом выступает система функций Уолша.

Обобщённый ряд Фурье представляется формулой:

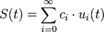
где это одна из базисных функций, а — коэффициент.

Разложение сигнала по функциям Уолша имеет вид:

В дискретной форме формула запишется следующим образом:

Определить коэффициенты можно, осуществив скалярное произведение раскладываемого сигнала на соответствующую базисную функцию Уолша:

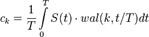
Следует учитывать периодический характер функций Уолша.

9. Интерполяция: спектральная трактовка, КИХ-фильтры для полиномиальной интерполяции 0- и 1-го порядка; использование полифазной структуры. Интерполяция – процесс цифр. обработки сигналов, приводящий к формированию сигнала y(nT) с повышенной частотой дискретизации из сигнала x(vT’)=x(vLT) с более низкой частотой дискретизации при определенных ограничениях на временные и спектральные изменения исх.сигнала.

Выделяют три разновидности процесса интерполяции ЦОС:

1. Увеличение частоты дискретизации осуществляется в соответствии с математическим понятием интерполяции;

2. При увеличении част.дискр. исходные отсчеты дискретного сигнала x(vT’) оказываются утерянными, однако отсчеты выходного сигала y(nT) могут рассматриваться как отсчеты исходного аналогового сигнала x(t), из которого путем дискретизации с интервалом T’ образован исходный дискретный сигнал x(vT’). В этом случае форма огибающей сигналов x(vT’) и y(nT) (и спектр) не изменяются;

3. Увеличение част.дискретизации приводит к изменению формы интерполируемого сигнала, однако модуль спектра не меняется.

Д-дискретизатор c интервалом дискретизации T’=LT., ИИ-идеальный интерполятор увеличивает част.дискр. в целое число L.После ИИ сигнал можно рассматривать, как результат дискретизации исх.аналогового сигнала x(t) с интервалом дискретизации T=T’/L., Hφ-дискретная система с частотной хар-кой .

Частотная интерполяция процесса с целым коэффициентом L:

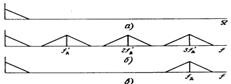
а)спектр исходного аналогового сигнала. б)спектр дискретизированного сигнала с часотой дискретизаии fд. в)спектр дискретизированного сигнала с частотой дискретизации fд’=3fд.

Т.О. процесс повышение частоты дискретизации (интерполяции) – преобразование спектра от б) к в), то есть подавление «лишних» частотных составляющих исх.спектра.

Увеличение частоты дискретизации исх.сигнала в нужное число раз L осуществляет экспандер частоты дискретизации (ЭЧД).

Использование полифазной структуры при интерполяции с использованием КИХ-фильтров. Особенность данной структуры в том, что вместо одного фильтра, работающего на высокой частоте дискретизации, используется несколько фильтров, работающих на низкой частоте. Полифазный фильтр представляет собой набор небольших фильтров, работающих параллельно, каждый из которых обрабатывает только подмножество отсчётов сигнала (если всего имеется N фильтров, каждый фильтр будет обрабатывать только каждый N-й отсчёт). Эквивалентная схема полифазной структуры:

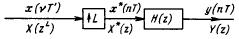
Проектирование КИХ-фильтров для полиномиальной интерполяции 0- и 1-го порядка.

Нулевой порядок. При вычислении очередного отсчета вых сигнала y(nT) с интервалом дискретизации T исп-ся только один отсчет входного интерполируемого сигнала x(vT’) с интервалом дискретизации T’. При увеличении частоты дискретизации в L раз отсчет сигнала x(vT’) повторяется L раз на тактах n=vL, vL+1, …,vL+L-1:

y(nT)=x(vT’), n=vL, vL+1, …,vL+L-1, v=0,1,2,…

Процесс интерполяции нулевого порядка показан на след.рис, где Tз-задержка, вносимая фильтром.

Передаточная функция фильтра

Реализация однородного фильтра: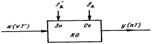

Входной сигнал x(vT’) записывается в регистр RG с частотой fд’=1/T’, а считывание сигнала y(nT) производится с частотой fд=Lfд’=1/T. Первый порядок(линейная интерполяция). Пусть дан сигнал x(n)=cos(2πn∙0,125). Между кажд. отсчетом исх. сигнала вставляется L-1 отсчетов (повышение част.дискретизации). Записывается передаточная функция

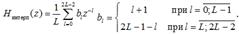
Далее выполняется фильтрация сигнала с L-1 отсчетами.Фильтр с вышеуказанной ПФ называется триангулярным. Такому фильтру соответствует последовательное соединение двух однородных фильтров с ПФ:

10. Децимация: спектральная трактовка, КИХ-фильтры для полиномиальной децимации 0- и 1-го порядка; использование полифазной структуры.Децимация - процесс уменьшения частоты дискретизации сигнала.

Рассмотрис сигнал x(t), модуль его спекта а).

x(nT)-дискретизированный сигнал с интервалом дискретизации T, его модуль его спектра в первом случае б), во втором г).

x(лямбдаT)-дискретизированный сигнал x(t) с интервалом дискретизации T’=MT.(M=2), его модуль спектра в первом случае в), во втором д).

Случай 1. При дискретизации с частотой wд1 выполнилось условие условие wд1 2Мwmax.(в нашем случае wд1 4wmax). Сигнал можно восстановить, так как спектр не перекрывается.

Случай 2. При дискретизации с частотой wд2 не выполнилось условие условие wд2 2Мwmax. Сигнал восстановить нельзя, т.к спектр накладывается.

Для выполнения операции децимации в целое число раз М необходимо, чтобы частота дискретизации wд сигнала x(nT), подлежащего децимации, удовлетворяло условию wд 2Мwmax.

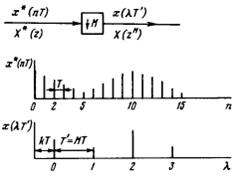
Операция децимации осуществляется с помощью компрессора частоты дискретизации(КЧД)(рис слева). КЧД представляет собой ключ, который замыкается в моменты t=nMT=лямбдаT’, то есть из входного сигнала x*(nT) с интервалом дискретизации Т берется только каждый М-й отсчет и формирует сигнал x(лямбдаT’)= x*(лямбдаМТ) с интервалом дискретизации Т=МТ

Использование полифазной структуры при децимации с использованием КИХ-фильтров. Данная структура содержит М параллельных ветвей обработки, в каждой из которых находится фильтр, работающий на «низкой» (выходной) частоте дискретизации. Уравнение, описывающее полифазную структуру децимации:

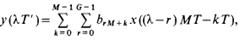
Где М-целочисл.коэффициент,

G-целое число, r=0, 1,…,M-1.

Т.е. выходная последовательность y(лямбдаT’) схемы есть сумма М последовательностей yk(лямбдаMT’), k=0,1,…,M-1, каждая из которых есть в свою очередь результат фильтрации последовательности yk*(лямбдаMT’)=x(лямбдаМТ-kT) дискретным фильтром с ПФ Hk*(zM) и импульсной характеристики brk=brM+k, причем отсчеты импульсной характеристики k-го фильтра есть отсчеты импульсной характеристики bl фильтра-прототипа,взятые через М-1 отсчет.

Проектирование КИХ-фильтров для полиномиальной децимации 0- и 1-го порядка.

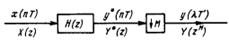
Схема уменьшения частоты дискретизации

Нулевой порядок. В качестве фильтра используется однородный, передаточная функция которого:

АЧХ однородного фильтра

Условие, при котором выбирается порядок фильтра: N=k*M.

Первый порядок. В качестве фильтра используется триангулярный с ПФ.

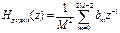
с АЧХ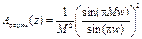

Дата добавления: 2015-07-02