Влияние скорости хода и курса корабля на частоту возмущающих сил и моментов

Рассмотрим более подробно формулу (3.26) для определения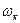

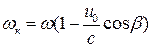. (3.26)

Величина кажущейся частоты, как мы видим, зависит от соотношения скорости хода корабля u ₀и скорости волны с, а также от курсового угла β. Именно с этой частотой волны будут воздействовать на корабль, т.е. она будет являться частотой возмущающих сил и моментов.

Рассмотрим несколько основных положений корабля относительно волн.

1. Курсовой угол β = 0. В соответствии с рис.3.1 волны и корабль идут

в одном направлении – попутное волнение. При этом получится cos β = 1 и .

Если u ₀ = с, корабль относительно волны не движется. Получится, что 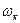= 0, т.е. частота возмущающих сил и моментов равна 0. Такое положение называется статической постановкой корабля на волну.

Если u ₀ = 0, получится = .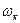

Если взять u ₀ > с, получится как бы отрицательная кажущаяся частота, но физически это означает, что корабль обгоняет волны. В этом случае

частоту надо определять по абсолютной величине, т.е. .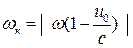

2. Курсовой угол β = π/2. В этом случае cos β = 0 и = .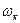

3. Курсовой угол β = π. В этом случае cos β = -1 и .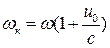

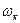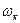Если задать u ₀ = с, получится = 2 , при u ₀ = 2 с получается = = 3 и т.д.

Таким образом, диапазон изменения 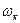простирается от 0 до практически бесконечного значения, и всегда возможно, что кажущаяся частота станет равной собственной частоте либо бортовой качки, либо килевой и верти-кальной, т.е. всегда возможно возникновение резонансных режимов для того или иного вида качки. Эти режимы можно определить из равенств 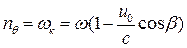или . Но большие амплитуды качки возникают не только при резонансах, а вообще в ближайших зонах, примерно при 0,7 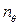≤ ≤ 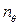1,3 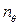и 0,7 п_ψ ≤ п_ψ ≤ 1,3 п_ψ. Это прекрасно видно при рассмотрении амплитудно – частотных характеристик.

Чтобы судоводитель мог избежать попадания в резонансные зоны, в про-цессе проектирования для него рассчитывается альбом круговых диаграмм, форма которых была предложена В.Г. Власовым. На рис. 5.1 приведена круговая диаграмма, на которой в виде заштрихованных зон видны неблагоприятные сочетания u ₀ и β, при которых качка будет усиленной. Судоводителю необходимо выбирать такую скорость хода или направление движения, чтобы уйти из опасной зоны.

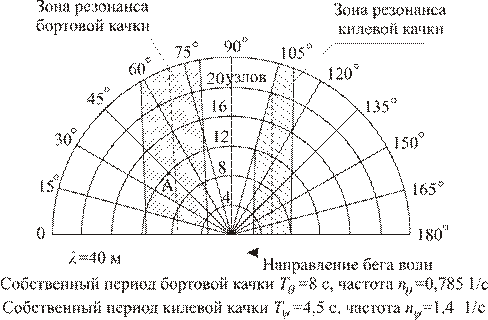
Рис. 5.1. Круговая диаграмма Власова

На диа­грамме направление гребней — вертикальное, направление бега волн - справа налево. Исходящие из центра лучи представляют направления скорости хода корабля, а радиусы концентрических окружностей - величины скорости хода корабля в узлах. Курсовые углы показаны через 15°. Диаграммы симметричны относительно прямой 0—180°, и поэтому вычерчиваются только половины диаграммы. Каждая диаграмма строится для определенной длины волны λ и определенных периодов или частот бортовой и килевой качки корабля.

Каждому значению скорости хода корабля u ₀и курсового угла β на диаграммах соответствует определенная изображающая точка и, наоборот, каждой точке диаграммы соответствуют определенные зна­чения скорости хода и курсового угла. Например, скорости 12 узл. и углу θ =45° отвечает точка А. При постоянной ско­рости хода и меняющемся курсовом угле изображающая точка перемещается по окружности; при неизменном курсовом угле и меняющейся скорости та же точка перемещается вдоль луча. Если при одновре­менном изменении скорости и курса произведение u ₀ cos β остается постоянным, то точка А перемещается по вертикали.

Диаграммы вычерчиваются для ряда длин волн и собственных частот или периодов качки, возможных при эксплуатации данного корабля. Собственная частота килевой качки в условиях плавания корабля меняется очень мало, поэтому для всех диаграмм ее можно выбрать постоянной (какой-либо средней).

Волнение предполагается регулярным, поэтому на реальном морском волнении точность диаграммы может снижаться. Но, если учесть, что судо-водитель длину будет волны оценивать визуально, период качки также опре-делять приближенно, для грубой ориентировки точности диаграмм вполне хватает. Далее необходимо использовать хорошую морскую практику.

Иногда, если не удается получить необходимые значения скорости хода или значительно отклоняться от заданного направления движения, кораблю приходится двигаться зигзагом.

Дата добавления: 2015-07-02