Аппаратурная реализация циклических кодов

Декодирование циклических кодов

Для обнаружения и исправления ошибок принятая комбинация делится на образующий многочлен g(х). Если остаток R(х) = 0, значит, комбинация принята без ошибок. Наличие остатка свидетельствует о том, что комбинация принята искаженной. Значение остатка совпадет с одним из опознавателей матрицы Н, который и укажет на местоположение ошибки по вектору ошибок.

1011

1011

1011

011 - ошибка в четвертом разряде

Если ошибка содержится в одном из поверочных разрядов, то одночлен одиночной ошибки будет иметь степень, меньшую, чем степень образующего многочлена и совпадет с остатком от деления. При этом номер разряда остатка прямо укажет на номер искаженного поверочного разряда.

1011

1011

1011

1011

010 - ошибка во 2-м контрольном разряде

Существует более общий алгоритм обнаружения и исправления ошибок:

1. Принятая комбинация делится на образующий многочлен g(x). Если остаток R(x)<>0 то определяется вес остатка w. Если вес остатка равен или меньше числа исправляемых ошибок t (w<=t), то принятую комбинацию складывают по модулю 2 с остатком и получают исправленную комбинацию.

2. Если w>t, то производится циклический сдвиг на один символ влево и полученная после такого сдвига комбинация снова делится на образующий многочлен. Если вес полученного остатка w<=t, то циклически сдвинутую комбинацию складывают с остатком и затем после сложения циклически сдвигают в обратную сторону вправо на один символ (возвращают на прежнее место). В результате получаем исправленную комбинацию.

3. Если после циклического сдвига на один символ по прежнему w>t, то производят дополнительные циклические сдвиги влево. При этом после каждого сдвига осуществляется деление сдвинутой комбинации на g(x) и проверяется вес остатка. При w<=t сдвинутую комбинацию складывают с остатком и производят обратных циклических сдвигов вправо столько, сколько было сделано влево.

Пример 5.7. Необходимо проверить принятый код 1101110, для g(x)=1011 и t=1.

1. Принятый код 1101110 делим на g(x), находим остаток R(x)=111, w=3

2. Код 1101110 сдвигаем влево на один разряд, получаем 1011101. Делим на образующий многочлен g(x). Находим остаток R(x)=101, вес w=2

3. Снова производим сдвиг влево, получаем 0111011. Делим на g(x). Остаток R(x)=001. w=1

4. Складываем сдвинутую комбинацию с остатком 0111011+001=0111010

5. Производим два циклических сдвига вправо

0111010 -> 0011101 ->1001110

В результате получили исправленную комбинацию.

Циклические коды реализуются с помощью сдвиговых регистров. Схема кодирования (образуется с помощью деления на образующий многочлен):

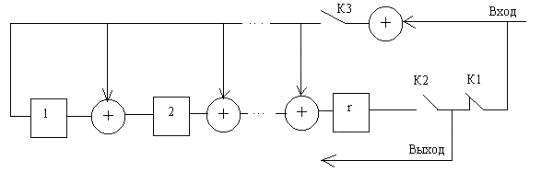
Рис. 5.7. Схема кодирования

Ключи к1 и к2 первоначально замкнуты, а ключ к3 – разомкнут. Исходная комбинация через ключ к1 поступает на выход и через входной сумматор на сдвиговый регистр, где и образуется контрольные символы. Затем ключ к2 замыкается, а к1 и к3 размыкаются. Контрольные символы подаются на выход в след, за информационными символами.

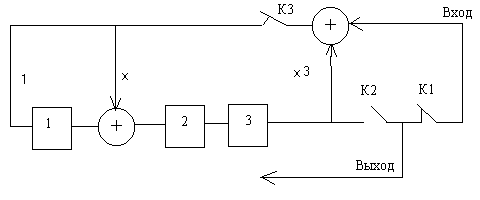
Рис.5.8. Схема кодирования методом деления на образующий многочлен g(x)=x³+x+1

Вх

Пример 5.8. Пусть на вход подается комбинация 1101. Последовательность деления представлена в таблице. В результате на выходе будет получена комбинация 1101001

Вх

Пример 5.9. Пусть на вход подается комбинация 1001. В результате деления будет получена комбинация 1001011

Схема декодирования (образуется с помощью деления на образующий многочлен):

Рис.5.9. Схема декодирования циклического кода. АО - анализатор ошибок.

Исходная комбинация подается в буферный регистр и одновременно через ключ в декодирующий регистр. Если с приходом последнего символа, зафиксирован нулевой остаток, то ошибок нет, и, если не нулевой, то есть ошибка. Принятая комбинация подается через выходной сумматор, и искаженный сигнал исправляется анализатором ошибок (АО).

Рис.5.10. Пример схемы декодирования методом деления на полином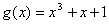

Пример 5.10. Пусть декодирующий регистр построен методом деления на образующий полином .

Пусть на вход подается комбинация 1101001

Вх

В результате деления получился нулевой остаток, следовательно, ошибок нет.

Теперь пусть на вход подается комбинация с ошибкой 1100001

Вх

В результате получился не нулевой остаток 110. Отключим ключ и начнем выводить комбинацию из буферного регистра. На четвертом такте

№
---

анализатор ошибок подаст на выходной сумматор сигнал исправления. Ошибка будет исправлена.

Для исправления многократных ошибок используется произведение образующих многочленов: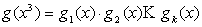

Таблица 5.3. Неприводимые полиномы

g(x)	Полином	g(x)	полином
g(x)	x+1	g1(x^6)	x^6+x+1
g(x^2)	x^2+x+1	g2(x^6)	x^6+x^3+1
g1(x^3)	x^3+x^1+1	g3(x^6)	x^6+x^5+1
g2(x^3)	x^3+x^2+1	……………	……………
g1(x^4)	x^4+x+1	g1(x^7)	x^7+x+1
g2(x^4)	x^4+x^3+1	g2(x^7)	x^7+x^3+1
g3(x^4)	x^4+x^3+x^2+x+1	g3(x^7)	x^7+x^3+x^2+x+1
g1(x^5)	x^5+x^2+1	……………	……………
g2(x^5)	x^5+x^3+1	g1(x^8)	x^8+x^4+x^3+x+1
g3(x^5)	x^5+x^3+x^4+x+1	g2(x^8)	x^8+x^4+x^3+x^2+1
g4(x^5)	x^5+x^4+x^2+x+1	……………	……………
g5(x^5)	x^5+x^4+x^3+x+1	g1(x^9)	x^9+ x+1
g6(x^5)	x^5+x^4+x^3+x^2+1	g2(x^9)	x^9+x^4+ 1

Дата добавления: 2015-07-02