Возможные ошибки измерения

В парной регрессии выбор вида математической функции yх=f(x), может быть осуществлен графическим, аналитическим, экспериментальным методами.

Наиболее наглядным методом является графический. Он основан на поле корреляции.

Основные типы кривых, используемых при количественной оценке связей, представлены на рис. 1.

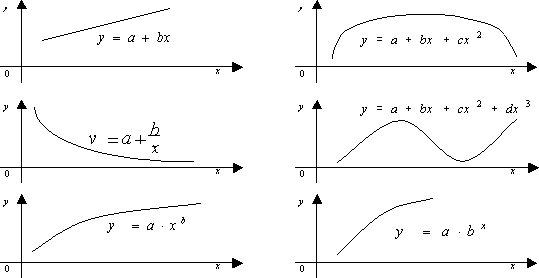
Рис 1. Основные типы кривых, используемые при количественной оценке связей между двумя переменными

Кроме уже указанных используют также и другие типы кривых, например:

Тогда зависимость потребления электроэнергии от объема продукции можно выразить уравнением регрессии вида: y = a+bx

Если разделим обе части уравнения на величину объема выпускаемой продукции (х), то получим выражение зависимости удельного расхода электроэнергии на единицу продукции (z = y/x) от объема выпущенной продукции (х) в виде уравнения гиперболы:

z = b+a/x

При обработке информации на компьютере выбор вида уравнения регрессии осуществляется экспериментальным методом, т.е. путем сравнения величины остаточной дисперсии Dост, рассчитанный при разных моделях.

В реальных условиях, как правило, всегда имеет место некоторое отклонение точек результативного признака относительно линии регрессии, обусловленное, присутствием случайного члена ε.

Поэтому для уравнения регрессии вычисляется величина суммы отклонений (y-yx), где y – фактические значения результативного признака, yx – расчетные значения, полученные по уравнению регрессии.

Чем меньше величина Dост, тем лучше уравнение регрессии описывает рассматриваемую корреляционную связь. Из разных математических функций выбирается та, для которой Dост является min.

В случае, когда Dост оказывается примерно одинаковой для нескольких функций, то предпочтение отдается более простым видам функций.

Обычно число наблюдений должно в 6-7 и более раз превышать число рассчитываемых параметров при переменной х.

Дата добавления: 2015-07-02