Пример. По данным о сумме активов (y), кредитных вложений (х1) и величине собственного капитала (х2) коммерческих банков одного из регионов РФ необходимо построить

По данным о сумме активов (y), кредитных вложений (х₁) и величине собственного капитала (х₂) коммерческих банков одного из регионов РФ необходимо построить множественное уравнение связи.

Номер банка	Сумма активов, млн.руб. Y	Кредитные вложения, млн. руб. х1	Собственный капитал, млн.руб. х2	у*х1	х1^2	х1*х2	х2^2	y*x2
Итого				21 956 214	14 266 159	1 510 415	175 876	2 534 726

Система нормальных уравнений имеет вид:

na₀ + a₁Sx₁ + a₂Sx₂ = Sy

a₀Sx₁ + a₁Sx₁² + a₂S x₁x₂ = Syx₁

a₀Sx₂ + a₁S x₁x₂ + a₂S x₂² = Syx₂

7a₀ + 8671a₁ + 1046a₂ = 14757

8671a₀ + 14266159a₁ + 1510415a₂ = 21956214

1046a₀ + 1510415a₁ + 175876a₂ = 2534726

Отсюда: a₀ - 443,4; a₁= 0,0368; a₂= 16,77

Y_x1,x2 = -443.4 + 0.0368x₁ + 16.77x₂

Расчеты показали, что с увеличением кредитных вложений на 1млн.руб. и собственного капитала банков на 1млн.руб. стоимость их активов возрастает соответственно в среднем на 0,0368 и 16,77 млн.руб.

В случае линейной двухфакторной связи коэффициент множественной корреляции может быть рассчитан не только на основе факторной и общей дисперсий, но и по следующей формуле:

,

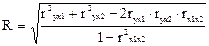где r – линейные коэффициенты корреляции (парные), а подстрочные индексы показывают, между какими признаками они исчисляются.

Величина D = R² называется коэффициентом множественной детерминации. Она показывает, какая часть общей дисперсии результативного признака обусловлена вариацией признаков-факторов, включенных в уравнение множественной регрессии.

Сопоставить факторные признаки по степени их влияния на признак результативный на основе коэффициентов регрессии не представляется возможным из-за различия единиц измерения и разной степени их колеблемости.

Для устранения таких различий при интерпретации модели применяется целая система показателей:

- частные коэффициенты эластичности (Э_i);

- бета-коэффициенты (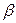 _i);

- дельта-коэффициенты ( _i).

Частные коэффициенты эластичности рассчитываются по формуле:

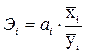_, (2)

где a_i – коэффициент регрессии при i-м факторном признаке;

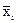– среднее значение i-го факторного признака;

– среднее значение результативного признака.

Частные коэффициенты эластичности показывают, на сколько процентов в среднем изменяется анализируемый показатель y с изменением на один процент соответствующего фактора x при фиксированном положении (на среднем уровне) всех прочих факторов, входящих в модель. Однако частные коэффициенты эластичности не учитывают степень колеблемости факторов.

Для выявления факторов, в которых заложены наиболее крупные резервы изучаемого показателя, необходимо учесть различия в степени варьирования вошедших в модель факторов. С этой целью используется другой показатель – бета-коэффициент (b-коэффициент), который вычисляется по формуле:

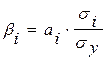, (3)

где si – среднее квадратическое отклонение i-го фактора;

sy – среднее квадратическое отклонение результативного признака.

Бета-коэффициент показывает, на какую часть среднего квадратического отклонения изменяется результативный признак с изменением соответствующего факторного признака на одно среднее квадратическое отклонение при фиксированных на постоянном уровне значениях остальных факторных признаков.

Вместе с тем с помощью частных коэффициентов эластичности и b-коэффициентов нельзя непосредственно оценить долю влияния каждого фактора в суммарном влиянии всех факторов. Для этой цели используются дельта-коэффициенты. Они рассчитываются по формуле:

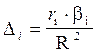, (4)

где ri – коэффициент парной корреляции i-го факторного признака с результативным признаком;

R² – коэффициент множественной детерминации.

При этом соблюдается следующее условие:

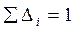. (5)

Дата добавления: 2015-07-02