Оценка эксперта: 4 балла

Пример 6.

Оценка эксперта: 2 балла.

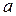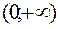Найдите все значения , при каждом из которых уравнение на промежутке имеет более двух корней.

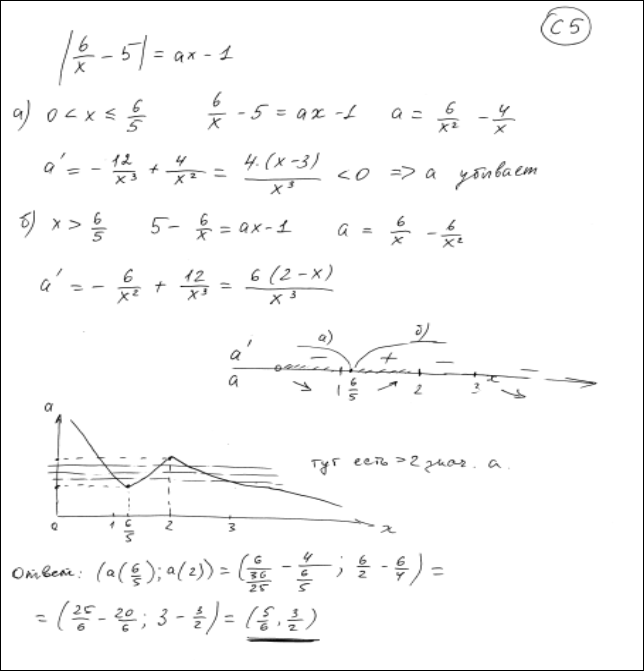
Комментарий. Редкий и довольно неожиданный способ решения, для применения которого нужен специальный навык. К недостаткам можно отнести тот факт, что на рисунке – гладкая кривая, в то время как в точке минимума функция, очевидно, не имеет производной. Впрочем, ни на рассуждение, ни на ответ это не влияет.

§7 Критерии проверки и оценка решений заданий №21 вариантов КИМ ЕГЭ-2015

Содержательно задание №21 (бывшее С6) проверяет в первую очередь не уровень математической (школьной) образованности, а уровень математической культуры. Вопрос формирования соответствующей культуры – вещь деликатная и, в целом, формируемая на протяжении нескольких лет.

В то же время, изменения в формате ЕГЭ связаны, в частности, с тем, что это задание по своему тематическому содержанию стало элементарнее, а для его решения, формально, достаточно простейших сведений. По этой причине, например, в ЕГЭ-2014 более 16% участников приступили к решению задания С6 и 7% получили положительные баллы, т.е. оно перестало отпугивать выпускников.

В связи этим хотелось бы подчеркнуть, что никаких фактов из теории чисел типа теоремы Вильсона, чисел Мерсенна, малой теоремы Ферма, теории сравнений и т.п. для решения заданий №21(С6) не требуется. Тот, кто эти факты знает, разумеется, может их использовать, но, подчеркиваем, при решении всегда можно обойтись и без них.

Условия задания №21, как и прежних заданий С6, разбиты на пункты. По существу, задача разбита на ряд подзадач (частных случаев), последовательно решая которые можно в итоге справится с ситуацией в целом. Как правило, решение п. а весьма несложно и использует умение сконструировать некоторый конкретный пример. В соответствии с таким делением условий, критерии, начиная с 2011 года стали более формализованными. Их текст практически никак не использует тематическую или содержательную фабулу конкретной задачи. Такие изменения были предприняты для большей согласованности и унификации выставляемых экспертами оценок.

Ниже процитированы три задачи из материалов ЕГЭ 2014, 2012 и 2011 гг., их решения, ответы и критерии проверки, действовавшие на соответствующий год проведения экзамена. Интересно отметить, что в самой ранней задаче 3 еще не было деления на пункты. В задаче 1 в скобках приведены также числовые параметры версии этой же задачи из другого варианта. Далее в Части 1 приведены 6 примеров решений этих задач на ЕГЭ вместе с комментариями по оценке и самими оценками. Подчеркнем, что каждая задача оценивалась по критериям соответствующего года проведения ЕГЭ. В Части 2 также приведены примеры решений этих же задач, но оценки верности этих решений следует проверить самостоятельно. В Части 3 для проведения зачета выбраны только решения задачи 1 (ЕГЭ-2014) и ее версий.

Задача 1.

Семь экспертов оценивают кинофильм. Каждый из них выставляет оценку — целое число баллов от 0 до 10 (от 1 до 15) включительно. Известно, что все эксперты выставили различные оценки. По старой системе оценивания рейтинг кинофильма — это среднее арифметическое всех оценок экспертов. По новой системе оценивания рейтинг кинофильма вычисляется следующим образом: отбрасываются

наименьшая и наибольшая оценки и подсчитывается среднее арифметическое пяти оставшихся оценок.

а) Может ли разность рейтингов, вычисленных по старой и новой системам оценивания, равняться ? ()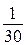

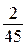б) Может ли эта разность рейтингов, вычисленных по старой и новой системам оценивания, равняться ? ()?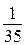

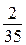в) Найдите наибольшее возможное значение разности рейтингов, вычисленных по старой и новой системам оценивания.

Решение. Обозначим рейтинг кинофильма, вычисленный по старой системе оценивания, через , а рейтинг кинофильма, вычисленный по новой системе оценивания, через .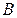

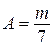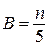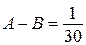а) Заметим, что , , где и — некоторые натуральные числа. Значит, . Если , то 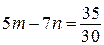, что невозможно. Таким образом, разность рейтингов, вычисленных по старой и новой системам оценивания, не может равняться .

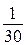б) Например, для оценок экспертов 0, 1, 2, 4, 7, 8, 9 разность рейтингов, вычисленных по старой и новой системам оценивания, равна

.

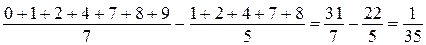в) Пусть 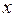— наименьшая из оценок, 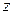— наибольшая, а — сумма остальных пяти оценок. Тогда

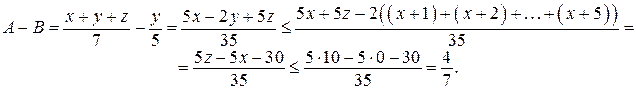
Для оценок экспертов 0, 1, 2, 3, 4, 5, 10 разность равна . Значит, наибольшее возможное значение разности рейтингов, вычисленных по старой и новой системам оценивания, равно .

Ответ: а) нет; б) да; в) .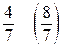

Содержание критерия, задача №1	Баллы
Верно получены все перечисленные (см. критерий на 1 балл) результаты
Верно получены три из перечисленных (см. критерий на 1 балл) результатов
Верно получены два из перечисленных (см. критерий на 1 балл) результатов
Верно получен один из следующих результатов: — обоснованное решение п. а; — пример в п. б; — искомая оценка в п. в; — пример в п. в, обеспечивающий точность предыдущей оценки
Решение не соответствует ни одному из критериев, перечисленных выше
Максимальный балл

Задача 2.

На доске написано более 27, но менее 45 целых чисел. Среднее арифметическое этих чисел равно 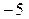, среднее арифметическое всех положительных из них равно 9, а среднее арифметическое всех отрицательных из них равно .

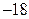а) Сколько чисел написано на доске?

б) Каких чисел написано больше: положительных или отрицательных?

в) Какое наибольшее количество положительных чисел может быть среди них?

Решение. Пусть среди написанных чисел 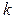положительных, 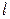отрицательных и 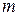нулей. Сумма набора чисел равна количеству чисел в этом наборе, умноженному на его среднее арифметическое, поэтому .

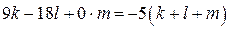а) Заметим, что в левой части каждое слагаемое делится на 9, поэтому 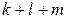— количество целых чисел — делится на 9. По условию 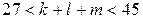, поэтому 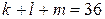. Таким образом, написано 36 чисел.

б) Приведём равенство 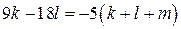к виду . Так как , получаем, что 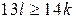, откуда 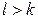. Следовательно, отрицательных чисел больше, чем положительных.

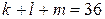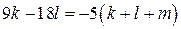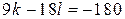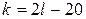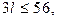
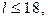
в(оценка) Подставим в правую часть равенства : , откуда . Так как , получаем: то есть положительных чисел не более 16.

в(пример) Приведём пример, когда положительных чисел ровно 16. Пусть на доске 16 раз написано число 9, 18 раз написано число 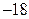и два раза написан 0. Тогда 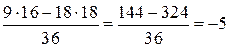, указанный набор удовлетворяет всем условиям задачи.

Ответ: а) 36; б) отрицательных; в) 16.

Содержание критерия, задача №2	Баллы
Верно выполнены: а, б, в (пример), в (оценка)
Верно выполнены три пункта из четырёх: а, б, в (пример), в (оценка)
Верно выполнены два пункта из четырёх: а, б, в (пример), в (оценка)
Верно выполнен один пункт из четырёх: а, б, в (пример), в (оценка)
Решение не соответствует ни одному из критериев, перечисленных выше
Максимальный балл

Задача 3.

Каждое из чисел 2, 3, …, 7 умножают на каждое из чисел 13, 14, …, 21 и перед каждым из полученных произведений произвольным образом ставят знак плюс или минус, после чего все 54 полученных результата складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге?

Решение.

1. Если все произведения взяты со знаком плюс, то их сумма максимальна и равна

.

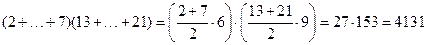2. Так как сумма оказалась нечетной, то число нечетных слагаемых в ней – нечетно, причем это свойство всей суммы не меняется при смене знака любого ее слагаемого. Поэтому любая из получающихся сумм будет нечетной, а значит, не будет равна 0.

3. Значение 1 сумма принимает, например, при такой расстановке знаков у произведений, которая получится при раскрытии следующих скобок:

.

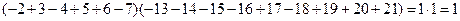Содержание критерия, задача №3	Баллы
Обоснованно получен правильный ответ
Ответ правилен, но недостаточно обоснован (например, не доказано, что либо сумма отлична от 0, либо что она может быть равна 1)
Верно найдено наибольшее значение суммы и доказано, что она всегда отлична от 0
Верно найдено только наибольшее значение суммы или только доказано, что она всегда отлична от 0
Решение не соответствует ни одному из критериев, перечисленных выше

Ответ: 1 и 4131.

Примеры оценивания решений заданий №21 (С6)

Дата добавления: 2015-07-02