
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Оценка эксперта: 2 балла
|
|
|
|
Комментарий.
Почти правильное решение. Есть один обидный (по невнимательности?) прокол: перед выплатой в июле оставшаяся половина долга также увеличивается на 5%
§6 Критерии проверки и оценка решений заданий №20 вариантов КИМ ЕГЭ-2015
Как это обычно бывает, задачи с параметром допускают весьма разнообразные способы решения. Наиболее распространенными из них являются:
- чисто алгебраический способ решения;
- способ решения, основанный на построении и исследовании геометрической модели данной задачи;
- функциональный способ, в котором могут быть и алгебраические, и геометрические моменты, но базовым является исследование некоторой функции.
Зачастую (но далеко не всегда) графический метод более ясно ведет к цели.
Ниже процитированы задачи двух типов из материалов ЕГЭ 2014 и 2013 гг., их решения, ответы и критерии проверки, действовавшие на соответствующий год проведения экзамена. Далее в Части 1 приведены 6 примеров решений этих задач на ЕГЭ вместе с комментариями по оценке и самими оценками. Подчеркнем, что каждая задача оценивалась по критериям соответствующего года проведения ЕГЭ. В Части 2 также приведены примеры решений этих же задач, но оценки верности этих решений следует проверить самостоятельно. В Части 3 для проведения зачета выбраны только решения задачи 1 (ЕГЭ-2014) и ее версий.
Задача 1 и ее версии по самому условию ориентирована не на геометрический способ решения: практически сразу «видна» новая переменная, относительно которой получается квадратное уравнение. Его исследование может быть проведено различными способами, из которых ниже выбран подход, по существу связанный с исследованием функции 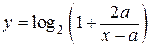 . В таком стиле, но без введения второго параметра, действовало, пожалуй, большинство участников ЕГЭ-2014, получивших положительные баллы за выполнение задания С5.
. В таком стиле, но без введения второго параметра, действовало, пожалуй, большинство участников ЕГЭ-2014, получивших положительные баллы за выполнение задания С5.
В решениях с ненулевыми баллами задачи 2 и аналогичных ей заданий чаще всего использовались графики. Из фиксированной на оси ординат точки проводились два луча: один – через точку «излома», другой – касательный к графику функции. Ответом являлся интервал между угловыми коэффициентами этих лучей. Так действовали многие, но большинство все-таки не получали оценки выше 1 балла.
Дело в том, что многие пропускали («это очевидно», «см. рис.») проверку того, что абсцисса точки касания действительно лежит правее абсцисс точки излома, т.е., что изображенная картинка соответствует истинному положению дел. По критериям, только при наличии такой проверки можно было выставлять более 1 балла (хватало и просто явного указания абсциссы точки касания). Аналогично, при алгебраическом подходе для получения 2-х баллов недостаточно просто приравнять к нулю дискриминант нужного квадратного уравнения: нужно еще указать, что соответствующий корень действительно больше абсциссы точки излома.
Задача 1
Найдите все значения 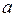 , при которых уравнение
, при которых уравнение
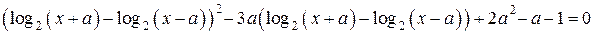
имеет ровно два решения.
Решение. Пусть 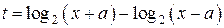 , тогда уравнение запишется в виде
, тогда уравнение запишется в виде 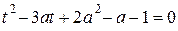 , откуда
, откуда 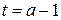 или
или 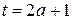 . Значит, решения исходного уравнения — это решения уравнений
. Значит, решения исходного уравнения — это решения уравнений 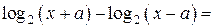
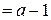 или
или 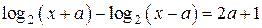 .
.
Исследуем, сколько решений имеет уравнение 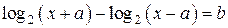 в зависимости от
в зависимости от 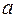 и
и 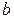 . При
. При 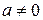 и
и 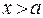
и 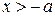 , то есть при
, то есть при 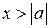 , левая часть определена и принимает вид
, левая часть определена и принимает вид 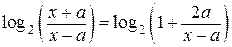 . При
. При 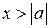 выражение
выражение 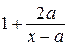 принимает
принимает
по одному разу все значения из промежутка 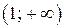 для
для 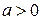 и принимает по одному разу все значения из промежутка
и принимает по одному разу все значения из промежутка 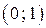 для
для 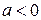 . Значит,
. Значит,
при 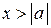 выражение
выражение 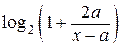 принимает по одному разу все значения из промежутка
принимает по одному разу все значения из промежутка 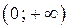 при
при 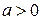 и принимает по одному разу все значения из промежутка
и принимает по одному разу все значения из промежутка 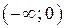 при
при 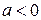 . Таким образом, уравнение
. Таким образом, уравнение 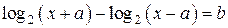 имеет одно решение при
имеет одно решение при 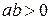 и не имеет решений при
и не имеет решений при 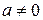 и
и 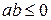 . При
. При 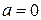 и
и 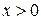 уравнение принимает вид
уравнение принимает вид 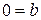 и либо имеет бесконечно много решений, либо не имеет решений.
и либо имеет бесконечно много решений, либо не имеет решений.
Уравнения 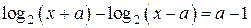 и
и 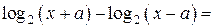
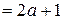 могут иметь общие решения при
могут иметь общие решения при 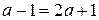 , то есть при
, то есть при 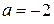 . При
. При 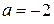 оба уравнения принимают вид
оба уравнения принимают вид 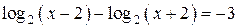
и имеют одно решение.
При других значениях 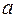 исходное уравнение имеет два решения, если оба уравнения
исходное уравнение имеет два решения, если оба уравнения 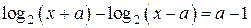 и
и 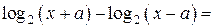
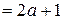 имеют по одному решению. Получаем систему неравенств:
имеют по одному решению. Получаем систему неравенств:
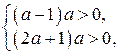
то есть 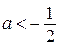 ;
; 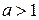 . Таким образом, исходное уравнение имеет ровно два решения при
. Таким образом, исходное уравнение имеет ровно два решения при 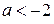 ;
; 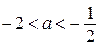 ;
; 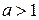 .
.
Ответ: 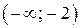 ;
; 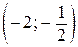 ;
; 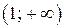 .
.
| Содержание критерия, задача №1 | Баллы |
| Обоснованно получен правильный ответ | |
С помощью верного рассуждения получено множество значений a, отличающееся от искомого только включением точек 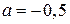 и/или и/или 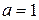
| |
С помощью верного рассуждения получен один из промежутков множества значений a: 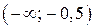 или или 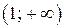 ; возможно, с включением граничных точек и/или исключением точки ; возможно, с включением граничных точек и/или исключением точки 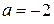
| |
Верно найдена хотя бы одна из граничных точек множества значений a: 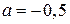 или или 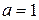 ;
ИЛИ
получено хотя бы одно из уравнений ;
ИЛИ
получено хотя бы одно из уравнений 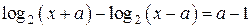 или или 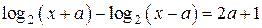
| |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
Задача 2.
Найдите все значения 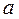 , при каждом из которых уравнение
, при каждом из которых уравнение
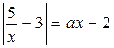
на промежутке 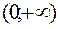 имеет более двух корней.
имеет более двух корней.
Решение. Рассмотрим функции 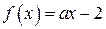 и
и 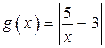 . Исследуем уравнение
. Исследуем уравнение 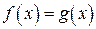 на промежутке
на промежутке 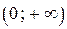 .
.
При 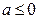 все значения функции
все значения функции 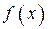 на промежутке
на промежутке 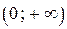 отрицательны, а все значения функции
отрицательны, а все значения функции 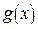 — неотрицательны, поэтому при
— неотрицательны, поэтому при 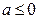 уравнение
уравнение 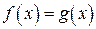 не имеет решений на промежутке
не имеет решений на промежутке 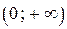 .
.
При 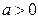 функция
функция 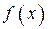 возрастает. Функция
возрастает. Функция 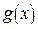 убывает на промежутке
убывает на промежутке 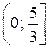 , поэтому уравнение
, поэтому уравнение 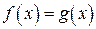 имеет не более одного решения на промежутке
имеет не более одного решения на промежутке 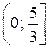 , причём решение будет существовать тогда и только тогда, когда
, причём решение будет существовать тогда и только тогда, когда 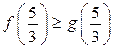 , откуда получаем
, откуда получаем 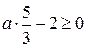 , то есть
, то есть 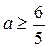 .
.
На промежутке 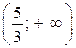 уравнение
уравнение 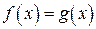 принимает вид
принимает вид 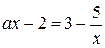 . Это уравнение сводится к уравнению
. Это уравнение сводится к уравнению 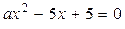 . Будем считать, что
. Будем считать, что 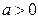 ,
,
поскольку случай 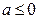 был рассмотрен ранее. Дискриминант квадратного уравнения
был рассмотрен ранее. Дискриминант квадратного уравнения 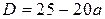 , поэтому при
, поэтому при 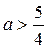 это уравнение не имеет корней; при
это уравнение не имеет корней; при 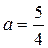 уравнение имеет единственный корень, равный 2; при
уравнение имеет единственный корень, равный 2; при 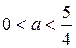 уравнение имеет два корня.
уравнение имеет два корня.
Если уравнение имеет два корня 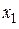 и
и 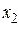 , то есть
, то есть 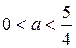 , то больший корень
, то больший корень 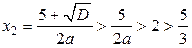 , поэтому он принадлежит промежутку
, поэтому он принадлежит промежутку 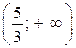 . Меньший корень
. Меньший корень 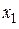 принадлежит промежутку
принадлежит промежутку 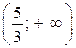 тогда и только тогда, когда
тогда и только тогда, когда
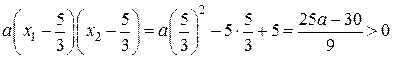 , то есть
, то есть 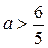 .
.
Таким образом, уравнение 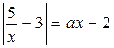 имеет следующее количество корней на промежутке
имеет следующее количество корней на промежутке 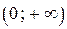 :
:
– нет корней при 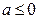 ;
;
– один корень при 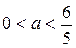 и
и 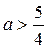 ;
;
– два корня при 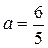 и
и 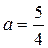 ;
;
– три корня при 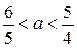 .
.
| Содержание критерия, задача №2 | Баллы |
| Обоснованно получен правильный ответ | |
| С помощью верного рассуждения получено множество значений a, отличающееся от искомого конечным числом точек | |
| С помощью верного рассуждения получены все граничные точки искомого множества значений a | |
| Верно найдена хотя бы одна граничная точка искомого множества значений a | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
Примеры оценивания решений заданий №20 (С5)
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 439; Нарушение авторских прав?; Мы поможем в написании вашей работы!