Алгебры

Лекция № 6

(лек.2 час + пр. зан 2час.+ сам. 4 час)

Алгеброй А называется совокупность < > множества М с заданными в нем операциями 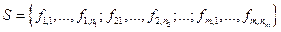, А = < М,S >, где множество М — носитель, S — сигнатура алгебры. Первый нижний индекс у идентификатора операции указывает ее местность.

Замечание. Для идентификации единого целого, содержащего объекты, которые имеют различное математическое строение, например множества и операций в нем, было предложено использовать термин совокупность и обозначать его угловыми скобками < >.

Пример.

Эти примеры очень важны, поскольку в них дается определение ряда фундаментальных алгебр.

Рассмотрим алгебры, в которых сигнатурой является двуместные операции. Обозначим эти операции символом f₂ ≡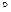

1. Если в алгебре А = < М,S > S = f₂, то такая алгебра называется группоидом А = < М, f₂ > или < М, >.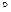

1.1. Если в алгебре А = < М, f₂ > f₂ есть операция типа умножения (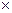), то такой группоид называется мультипликативным А = < М, >.

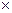1.2. Если в алгебре А = < М, f₂ > f₂ есть операция типа сложения (+), то такой группоид называется аддитивным А = < М, + >.

1.3. Если в алгебре G = < М, T > T - множество дуг (сигнатура графа), M - множество вершин (носитель графа), то такая алгебра называется графом.

2. Алгебра < М, 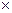, + >, которая по умножению является мультипликативным группоидом, по сложению - абелевой группой и умножение связано со сложением законами дистрибутивности, то эта алгебра называется кольцом.

2.1. Кольцо < М, 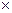, + >, в котором все отличные от нуля элементы составляют группу по умножению называется телом.

2.2. Тело < М, 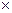, + >, у которого мультипликативная группа абелева, называется полем

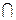3. Рассмотрим алгебры с тремя операциями: две двухместные f_2,1 и f_2,2 и одна одноместная f_1,1 < М, f_1,1, f_2,1, f_2,2 >, носителем которой является булеан М ≡ B(1) универсального множества 1, сигнатурой: операция объединения f_2,1 ≡ , пересечения f_2,2 ≡ и дополнения f_1,1 ≡ Ї.

3.1. Алгебра А = < B(1), , , Ї> называется алгеброй Кантора (решетка).

3.2. Алгебра А = < B(1), , , Ї> называется алгеброй Буля – дистрибутивная решетка с дополнениями.

Примечание. Эти две алгебры изоморфны.

Дата добавления: 2015-07-02