Алгебра отношений

Рассмотрим алгебру отношений, носителем которой является множество отношений, а сигнатура - операции: объединения, пересечения, разности и расширенное декартово произведение отношений.

, где Δ – расширенное декартово произведение отношений.

Объединением 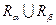двух совместимых отношений и 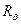является множество всех кортежей. Каждый, из которых принадлежит хотя бы одному из этих отношений.

Пример. Дано множество M = {a,b,c,d,e}. Тетрарное декартово произведение имеет степень – три, т.е. это M³. На нем заданы совместимые, т.е. одной и той же степени отношения и . Степени этих отношений равны: s(R_α) =3 и s(R_β) = 3. Сами отношения равны R_α = {<a,b,c>,(a,b,d),(b,c,e)} и R_β = {(a,b,d),(b,d,e),(c,d,e)}.

Объединением 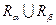двух совместных отношений и 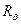является

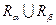= {(a,b,c),(a,b,d),(b,c,e),(b,d,e),(c,d,e)}

Пересечением двух совместных отношений и 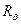является

= {(a,b,d)}

Разностью 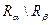двух совместных отношений и 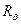является множество всех кортежей, принадлежащих отношению и не принадлежащих отношению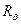

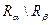= {(a,b,c),(b,c,e)}

Расширенным декартовым произведением двух совместных отношений и 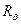является множество всех кортежей π таких, что π – конкатенация кортежа и кортежа . Конкатенация кортежей <a₁, a₂, …,a_n > и <b₁, b₂, …,b_m > является кортеж <a₁, a₂, …,a_n, b₁, b₂, …,b_m >.

= {(a,b),(с,d),(a,e)} 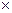{(a,b,c),(b,d,e)} = {(a,b,a,b,c), (a,b,b,d,e), (c,d,a,b,c), (c,d,a,b,c) (b,d,e),(c,d,e)}

ДОМАШНЕЕ ЗАДАНИЕ

Составить расписание сдачи зачетов трех групп ИСТАС. Написать каждое множество, дать общее описание каждого множества – структура, элементы, мощность.

Общие рекомендации. Работу выполнить с применением ЭВМ.

Структура работы.

Титульный лист. Тема: «Реляционная алгебра» Расписание сдачи зачетов

Формулировка задания.

Введение Частным случаем алгебраической системы является алгебра отношений, в которой носитель – это множество отношений R.

Расширением алгебры отношений является реляционная алгебра.

Дата добавления: 2015-07-02