Подалгебра», примеры

Алгебра множеств (алгебра Кантора)

Рассмотрим алгебру множеств (алгебру Кантора)

,

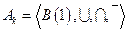носителем которой является булеан универсального множества 1, сигнатурой — операции объединения , пересечения 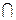и дополнения .

Для операций алгебры Кантора выполняются следующие законы:

коммутативности объединения и пересечения

, ,

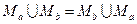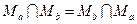ассоциативности объединения и пересечения

, ,

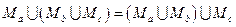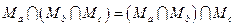дистрибутивности пересечения относительно объединения и объединения относительно пересечения

;

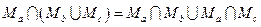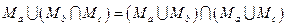
идемпотентности объединения и пересечения

;

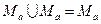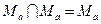
действия с универсальным 1 и пустым 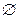множествами

, ,

;

; .

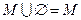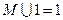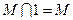
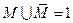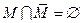де-Моргана

;

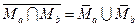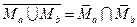
двойного дополнения

.

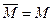Алгебра Кантора по аддитивной операции объединения и мультипликативной операции пересечения является абелевой полугруппой, так как для этих операций выполняются законы коммутативности и ассоциативности, но она не является группой, поскольку уравнения 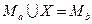; 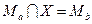не имеют решения, например для случая, когда множества не пересекаются: .

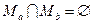Следовательно, алгебра Кантора по двуместным операциям и 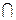не является кольцом. Эта алгебра принадлежит к другому классу фундаментальных алгебр - к классу решеток.

ВВЕДЕНИЕ В ТЕОРИЮ РЕШЕТОК

Частично упорядоченные множества

Алгебраическое понятие решетки тесно связано с отношением порядка, заданным на конечном множестве, и может быть определено следующим образом.

Определение: Множество S называется частично упорядоченным (ЧУМ), если на нем задано рефлексивное, транзитивной и антисимметричное бинарное отношение частичного порядка с.

Определение: ЧУМ называется линейно упорядоченным (цепью), если для любых x,y ∈ S или x ≤ y, или y ≤ x, либо выполняются оба эти отношения (x = y).

Любое конечное, линейно упорядоченное множество (A, ≤) можно представить следующим образом: a₁ ≤ a₂ ≤ a₃ ≤...≤ a_n. Мы можем также записать A как (a₁, a₂,..., a_n). Линейно упорядоченное множество можно изобразить графически диаграммой, в которой элементам множества соответствуют вершины. Из вершины а ведет дуга в вершину b, если a ≤ b и нет такого с, что a ≤ c ≤ b. Конечному линейно упорядоченному множеству (A, ≤) соответствует диаграмма вида (рис. 6.1)

Рис. 6.1.

На таких диаграммах не принято изображать петли, отображающие рефлексивность отношения ≤, и дуги, отображающие транзитивность этого отношения.

Утверждение: Частичное упорядочение на конечном множестве может быть представлено как объединение отношений линейного порядка на некоторых подмножествах данного множества

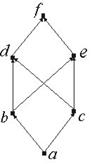
Любой частичный порядок можно представить изображением объединения множества диаграмм соответствующих линейно упорядоченных подмножеств. Полученная таким образом диаграмма называется диаграммой Хасса.

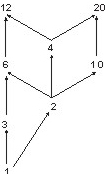
Рис. 6.2

Пример 6.1.

Пусть на множестве S={1,2,3,4,6,10,12,20} задано отношение с={(x, y):х делитель y}. Выделим все линейно упорядоченные подмножества S:(1, 3, 6, 12), (1, 2, 6, 12), (1, 2, 4, 12), (1, 2, 4, 20), (1, 2, 10, 20). Объединение диаграмм, построенных для этих подмножеств, дает диаграмму Хассе, показанную на рис. 6.2. Если задано (S, ≤) и B – подмножество S: B ⊆ S, можно определить верхнюю и нижнюю грани подмножества В.

Определение: Верхней гранью двухэлементного подмножества B={a,b}, a,b ∈ S, называется элемент h ∈ S, такой, что a ≤ h, b ≤ h. Соответственно,

нижней гранью двухэлементного подмножества B={a, b}, a, b ∈ S, называется элемент l ∈ S, такой, что l ≤ a, l ≤ b.

Определение: Если некоторая из верхних граней H подмножества B={a,b} удовлетворяет неравенству H ≤ h, где h - произвольная верхняя грань подмножества B={a,b}, то ее называют наименьшей верхней гранью (supremum) подмножества B и обозначают H = sup ({a,b}). Соответственно, если некоторая из нижних граней L подмножества B = {a, b} удовлетворяет неравенству l ≤ L, где l - произвольная нижняя грань, то ее называют наибольшей нижней гранью (infimum) подмножества B и обозначают L = inf ({a,b}).

Введенные понятия хорошо иллюстрируются на языке диаграмм Хассе:

x ≤ y, если и только если на диаграмме существует путь из вершины x в вершину y; верхняя грань подмножества B ={ a, b } на диаграмме соответствует вершине, в которую есть путь как из a, так и из b; нижняя грань подмножества B ={ a, b } соответствует вершине, из которой есть путь как в a, так и в b.

Пример 6.2.

Рассмотрим ЧУМ, представленное диаграммой Хассе на рис. 6.2. Подмножество B={3,6} имеет две верхние грани: h₁=6 и h₂=12, одна из которых является наименьшей: H=sup({3,6})=h₁=6. Это же подмножество имеет две нижние грани: l₁=1 и l₂=3, одна из которых является наибольшей: L=inf({3,6})=l₂=3. Подмножество B={6,4} имеет одну верхнюю грань h₁=12, которая, естественно, будет наименьшей верхней гранью H=sup ({6,4})=12, и две нижние грани l₁=2, l₂=1, одна из которых будет наибольшей: L=inf ({6,4})=l₁= 2. Подмножество B={6,10} имеет те же две нижние грани l₁=2, l₂=1 и ту же наибольшую нижнюю грань L=inf ({6,10})=l₁= 2, однако не имеет ни одной верхней грани

Решетки

Определение: Решеткой называется множество (S, ≤),в котором для любого двухэлементного подмножества B ⊆ S существует наименьшая верхняя грань H и наибольшая нижняя грань L. Иначе говоря, решетка - это алгебраическая система (S, ≤, ∧, ∨) с одним бинарным отношением ≤ и двумя бинарными операциями:

x ∧ y = L = inf ({x,y}) (конъюнкция),

x ∨ y = H = sup ({x,y}) (дизъюнкция),

определенными на множестве всех возможных двухэлементных подмножест B ⊆ S.

Решеткой называется ЧУМ A = < A;≤ >, в котором каждая пара элементов имеет супремум и инфинум. Для заданных элементов x,y A элемент inf{x,y} называется пересечением элементов x и y (обозначается x∧y), а sup{x,y} называется объединением элементов x и y (обозначается x∨y).

Пример 6.3.

Пусть задано множество S из трех различных целых чисел a, b, c. На этом множестве отношение ≤ (меньше или равно) задает частичный порядок. Предположим, что значения a, b, c таковы, что линейный порядок на множестве можно изобразить диаграммой на рис. 6.3. Если на множестве целых чисел S ={a, b, c} можно определить для любых x, y S две бинарные операции:

x ∧ y = inf ({x,y}) = min (x,y),

x ∨ y = sup ({x,y}) = max (x,y),

то это множество представляет собой решетку.

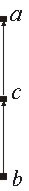
	a)	b)
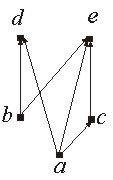
Рис. 6.3	Рис. 6.4

Возможны две причины, по которым частично упорядоченное множество (S, ≤) не является решеткой.

Причина 1.

Существует хотя бы одно из двухэлементных подмножеcтв B ⊆ S, не имеющее верхней или нижней грани. На диаграмме на рис. 6.4,а. подмножества {d, e},{d, c} не имеют верхней грани, подмножество {b,c} не имеет нижней грани.

По этой же причине не является решеткой ЧУМ из примера 6.1. Как следует из диаграммы Хасса (рис. 6.2), для любого двухэлементного подмножества B ⊆ S существует единственная наибольшая нижняя грань, однако для подмножеств {3,10},{3,20},{6,10},{6,20},{12,10},{12,20} не существует верхняя грань и, следовательно, для этих пар элементов не определена операция ∨.

Причина 2.

Существует хотя бы одно из двухэлементных подмножеств B ⊆ S, для которого наибольшая нижняя (наименьшая верхняя) грань не единственна. На диаграмме на рис. 6.4б все двухэлементные подмножества B ⊆ S имеют наименьшие верхние и наибольшие нижние грани, однако подмножество {b,c} имеет две несравнимые (не связанные отношением ≤) наименьшие верхние грани d и e; подмножество {d,e} имеет две несравнимые наибольшие нижние грани b и c.

Пример 1.4.

Рассмотрим множество V_n двоичных векторов длины n. Пусть на этом множестве задан частичный порядок с помощью отношения н ≤ щ, если в векторе щ единицы стоят на всех тех местах, на которых они стоят в векторе н (и, может быть, еще на некоторых). Например, при n = 3: (010) ≤ (011), однако векторы (010) и (100) несравнимы в смысле заданного отношения ≤.

Диаграмма Хасса для ЧУМ (V₃, ≤) показана на рис. 6.5. Определим на множестве (V_n, ≤) две бинарные операции: н ∧ щ - это вектор, в котором единицы стоят на тех и только тех местах, где единицы есть как в н, так и в щ; н∨ щ - это вектор, в котором единицы стоят на тех и только тех местах, где есть единицы либо в н, либо в щ.

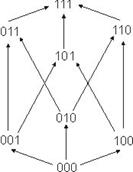
Рис.6.5

Например, при n = 3: (011) ∧ (101) = (001), (011) ∨ (101) = (111).

Простым перебором всех двухэлементных подмножеств нетрудно доказать, что множество (V₃, ≤, ∧, ∨) является решеткой.

Если на заданном ЧУМ (S, ≤) определены бинарные операции ∧ и ∨, то можно выявить ряд свойств этих операций,не зависящих от природы множества S. Эти свойства заключаются в следующем.

1. Любой элемент решетки x ∈ S идемпотентен по отношению к обеим операциям:

x ∧ x = x (аксиома А1а),

x ∨ x = x (аксиома А1б).

Очевидно, что наибольшая нижняя и наименьшая верхняя грани "подмножества" {x,x} есть x.

2. Обе операции коммутативны:

x ∧ y = y ∧ x (аксиома А2а),

x ∨ y = y ∨ x (аксиома А2б).

Доказательство коммутативности следует из самого определения этих операций. Как в определении операции ∧ (поиск наибольшей нижней грани двухэлементного подмножества {x,y}), так и в определении операции ∨ (поиск наименьшей верхней грани двухэлементного подмножества {x,y}) отношение порядка между элементами x и y сохраняется независимо от последовательности их написания в подмножестве {x,y}.

3. Обе операции ассоциативны:

(x ∧ y) ∧ z = x ∧ (y ∧ z) (аксиома А3а),

(x ∨ y) ∨ z = x ∨ (y ∨ z) (аксиома А3б).

Для доказательства ассоциативности операции ∧ необходимо убедиться в том, что (x ∧ y) ∧ z - наибольшая нижняя грань трехэлементного подмножества {x,y,z}, т.е. элемент L, являющийся результатом двойного применения операции ∨: L=(x ∨ y) ∨ z, меньше или равен любого из элементов x, y, z и в то же время больше или равен любого из элементов l, являющихся нижней гранью для элементов x, y, z: l ≤ x, l ≤ y, l ≤ z, l ≤ L.

Действительно, так как элемент L=(x ∧ y) ∧ z - это наибольшая нижняя грань подмножества {L_xy, z}, где L_xy = x ∧ y, то L ≤ L_xy и L ≤ z.

В свою очередь из отношения L ≤ L_xy= x ∧ y следует, что L ≤ x и L ≤ y.

Итак, можно считать установленным, что наибольшая нижняя грань удовлетворяет неравенствам L ≤ x, L ≤ y, L ≤ z. Но если нижняя грань удовлетворяет неравенствам L ≤ x и L ≤ y, то L ≤ x ∧ y= L_xy. Если выполняется еще и отношение L ≤ z, то L ≤ (x ∧ y) ∧ z = L_xy ∧ z = L, т. е. наибольшая нижняя грань L больше или равна любой из нижних граней. Из коммутативности операции ∧ следует:

x ∧ (y ∧ z) = x ∧ L_yz = L_yz ∧ x = (y ∧ z) ∧ x.

На основании предыдущих рассуждений это означает, что элемент L = x ∧ (y ∧ z) = (y ∧ z) ∧ x – наибольшая нижняя грань трехэлементного подмножества {y, z, x}. Поскольку подмножества {x, y, z}, {y, z, x} эквивалентны, то их наибольшие нижние грани L = (x ∧ y) ∧ z и L = x ∧ (y ∧ z) - совпадают. Тем самым ассоциативность операции ∧ доказана.

Ассоциативность операции ∨ может быть доказана аналогично

Дата добавления: 2015-07-02