Дистрибутивные решетки

Решетку (S, ≤, ∧, ∨), в которой операции ∧ и ∨ подчиняются двум дистрибутивным свойствам:

x ∧ (y ∨ z) = (x ∧ z) ∨ (x ∧ y), (аксиома А4а)

-дистрибутивность операции ∧ по отношению к операции ∨;

x ∨ (y ∧ z) = (x ∨ z) ∧ (x ∨ y), (аксиома А4б)

-дистрибутивность операции ∨ по отношению к операции ∧, называют дистрибутивной решеткой.

Покажем, что не все решетки являются дистрибутивными, на следующем примере.

Пример 1.5

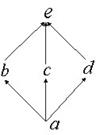
Рис. 6.6.

Исследуем на дистрибутивность решетку, приведенную на рис.6.6. Проверим свойство дистрибутивности операции ∧ по отношению к операции ∨

x ∧ (y ∨ z) = (x ∧ y) ∨ (a ∧ z) для x = b, y = d и z = c.

"Вычислим" левую часть этого выражения: x ∧ (y ∨ z) = b ∧ (d ∨ c) = b ∧ e = b.

Теперь "вычислим" правую часть выражения: (x ∧ y) ∨ (a ∧ z) = (b ∧ d) ∨ (b ∧ c) = a ∨ a = a.

Левая и правая части выражения различны, следовательно, рассмотренная решетка не дистрибутивна.

Пример 1.6

Исследуем на дистрибутивность решетку, приведенную в примере 1.4 (диаграмма на рис. 6.5).

Проверим свойство дистрибутивности операции ∨ по отношению к операции ∧:

x ∨ (y ∧ z) = (x ∨ z) ∧ (x ∨ y) для x = 011, y = 010, z = 110.

"Вычислим" левую часть выражения: 011 ∨ (010 ∧ 110) = 011 ∨ 010 = 011.

Теперь "вычислим" правую часть выражения: (011 ∨ 010) ∧ (011 ∨ 110) = 011 ∧ 111 = 011.

Совпадение обеих частей выражения означает, что операция ∨ дистрибутивна по отношению к операции ∧ для x = 011, y = 010, z = 110.

Полный перебор всех возможных "троек" элементов множества и проверка для каждой "тройки" обоих свойств дистрибутивности позволяют утверждать, что рассмотренная решетка дистрибутивна.

Свойства решетки зависят также от того, существуют ли в ней единичные элементы по отношению к операциям ∧ и ∨.

Определение: Пусть 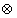- коммутативная бинарная операция на множестве S. Если существует элемент e ∈ S, для которого справедливо x 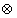e = e 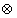x = x, то e называется единичным элементом по отношению к операции .

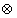Теорема 1.1.

Пусть 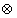- коммутативная бинарная операция на множестве S и существует единичный элемент по отношению к операции 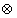. Тогда единичный элемент единственен.

Доказательство

Доказательство теоремы проведем "от противного".

Предположим, что существуют два различных единичных элемента e и e', тогда для любого x ∈ S справедливы равенства x 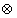e = x и x 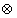e' = x. Подставим x = e' в первое равенство, x = e - во второе, тогда e' 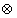e = e' и e 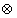e' = e. Но из свойства коммутативности операции 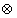следует 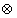e' e = e 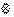e', поэтому e' = e, что и требовалось доказать.

Единичный элемент по отношению к операции ∧ (обозначим его e_∧) должен удовлетворять равенству x ∧ e_∧ = inf ({x,e_∧}) = x.

Иначе говоря, для произвольного элемента x ∈ S наибольшей нижней гранью двухэлементного подмножества {x,e} должен быть сам элемент x. Интуитивно ясно, что единичный элемент по отношению к операции ∧ должен быть наибольшим элементом решетки, а это, в свою очередь, означает, что элемент e_∧ должен быть наименьшей верхней гранью для любого подмножества {x,e_∧}.

Операция нахождения наименьшей верхней грани была ранее определена как бинарная:

H = sup({x,y}) = x ∨ y,

однако она может быть естественным образом расширена так, что результатом ее выполнения будет наименьшая верхняя грань всей решетки:

e_∧ = sup (S) = ∨_x∈S x = ∨ S,

иначе говоря, наибольший элемент решетки S.

Аналогичными рассуждениями нетрудно показать, что единичный элемент по отношению к операции ∨ (обозначим его e_∨) должен быть наибольшей нижней гранью решетки в целом:

e_∨ = inf (S) =∧_x∈S x = ∧ S,

иначе говоря, наименьший элемент решетки S.

Пример 1.7.

В решетке S из примера 1.4 (диаграмма на рис. 6.5) элементом e_∧ является вектор 111, а элементом e _∨ - вектор 000.

Таким образом, в соответствии с определением операций ∧ и ∨ как бинарных операций и теоремой 1.1 в решетке существуют единственные единичные элементы по отношению к операциям ∧ и ∨(e_∧ и e_∨ соответственно), обладающие следующими свойствами:

x ∧ e_∧ = e_∧ ∧ x = x (аксиомаА5а),

x ∨ e_∨ = e_∨ ∨ x = x (аксиома А5б).

Булева алгебра является расширением рассмотренной в 1.1 дистрибутивной решетки за счет добавления элемента, называемого дополнением.
В дальнейшем изложении будем пользоваться традиционными для литературы по булевой алгебре обозначениями единичных элементов. Для обозначения единичного элемента по отношению к операции конъюнкции вместо e_∧ будем использовать символ “ 1 ”. Единичный элемент по отношению к операции дизъюнкции обозначим вместо e_∨ символом “ 0 ”. Тогда аксиомы А5а и А5б, определяющие свойства этих единичных элементов, будут иметь следующий вид:

x ∧ 1 = 1 ∧ x = x;

x ∨ 0 = 0 ∨ x = x.

Дата добавления: 2015-07-02