III пример

II пример.

Во втором, математическом примере рассмотрим в качестве цели систему дифференциальных уравнений 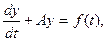решаемую для различных начальных условий и различных правых частей.

В этом случае имеем:

- входы: начальные условия, вектор правых частей f(t), значение t ₁, до которого необходимо интегрировать систему;

- выход: значение y(t ₁ ) = y ₁;

- неизменные параметры системы: матрица А;

- параметры состояния: вектор y;

- параметр процесса – t;

- правило S: решение дифференциального уравнения в зависимости от начальных условий, констант, правых частей и аргумента; y = y (t₀,, y₀,,A, f(t), t);

- правило V: подстановка в решение дифференциального уравнения значения t ₁; y ₁ = y\_{t=t 1} ;

- правило V: зависимость y ₁ = y(t₀,, y₀,, A, f(t), t ₁).

Третий пример информационный. Рассмотрим модель длительности переработки человеком текста в резюме. В этом случае:

- входы: объем текста, численная оценка его сложности;

- выход: длительность i составления резюме;

- неизменяемые параметры здесь будут соответствовать способностям данного человека: скорость осмысленного чтения текста и число повторных чтений в зависимости от его сложности усредненное число переделок резюме;

- параметры состояния определяют объем проделанной работы на данный момент t: объем изученного текста, объем составленной части резюме, оставшееся число переделок резюме;

- параметр процесса: стадия работы или время;

- правило S: зависимость объема проделанной работы, объема и сложности текста, способностей человека, времени;

- правило V: зависимость величины i от объема проделанной работы;

- привило V: зависимость величины i от объема текста, сложности и способностей данного человека.

Восемь рассмотренных составляющих кортежа не являются универсальными и обязательными. Это просто наиболее удобные на практике составляющие. Их может быть как больше (см., например, ниже системы управлением), так и меньше. Минимальное число составляющих имеет модель «черного ящика»:

Σ: { x⁺, x^--, V},

где х ^- = V (x ⁺).

Введение в рассмотрение «внутренности черного ящика» приводит к параметрам системы а, а типичное наличие процессов в системе – к параметрам состояния и процесса: у и t. На основании наличия процессов формулируются и правила S, V. Другими составляющими кортежа в определении модели могут быть входные случайные воздействия (представляющие собой часть входов х ⁺), характеристики структуры системы в отличие от характеристик элементов (выделенные из параметров а), некоторые свободные параметры модели, все множество значений которых должно быть учтено при расчете выходов (например, операциями взятия максимума, интегрированием), управление и введенные для целенаправленных систем.

Пример с моделью в виде системы дифференциальных уравнений интересен тем, что если считать выходом не значение функции у в точке t ₁, а саму функцию, то мы получаем совпадение операторов S и V. Операторное равенство для V при этом является просто переобозначением: х^- = у. Такое положение дел, когда выходом в системе служит параметр состояния, достаточно типично. Аналогичная ситуация уже отмечалась нами при определении цели системы в п. 1.1.5. Для этого случая можно вписать вместо (1.8) укороченный кортеж без правил S и V.

В примере с переработкой текста можно вполне обойтись без операторов S и V и строить сразу оператор V. Такая ситуация, когда удобно сразу. Без промежуточных стадий, искать основное правило V, тоже встречается нередко и аналогично случаю с системой дифференциальных уравнений ведет к кортежу без S и V. Кстати, именно этим объясняется наличие на первый взгляд «лишней» составляющей V в (1.8), ведь еще в определении этого правила мы подчеркнули, что оно выводило из предыдущих. Но именно типичность ситуации с отсутствием операторов S и V (или неудобство работы с ними) является основным оправданием практического удобства введения в кортежную запись модели.

Условность составляющих кортежа!

Часто даже при незначительных изменениях постановки задачи происходит переход величин из одной составляющей кортежа в другую. Так, некоторую мало меняющуюся величину в системе можно отнести и к параметрам системы а (сделав условно постоянной), и к параметрам состояния. Математическим путем заменены переменной нередко меняющиеся местами параметр процесса и один из параметров состояния. В ряде случаев могут возникать трудности с отнесением данной величины к параметрам состояния или выходным воздействиям.

Так, в примере о двигателе интересно разобрать вопрос о месте сил трения в кортеже. Напомним, что они отнесены к группе параметров состояния. Однако при широко используемой записи сил трения через кинематические величины и постоянные коэффициенты трения они могут быть выведены из рассмотрения с включением вместо них в список неизменяемых параметров системы указанных коэффициентов. Если же силы трения не зависят от кинематики, т.е. от состояния системы, то они могут считаться и входами. Если же нашей задачей будет исследование именно сил трения в двигателе, то эти силы станут выходами в системе.

Дата добавления: 2015-06-27