Дисперсия

Размах вариации

Характеристики рассеяния результатов измерений

Для математико-статистического анализа результатов выборки знать только характеристики положения недостаточно. Одна и та же величина среднего значе­ния может характеризовать совершенно различные выборки.

Поэтому кроме них в статистике рассматривают также характеристики рассеяния (вариации, или колеблемости) результатов.

Определение. Размахом вариации называется разница между наибольшим и наименьшим результатами выборки, обозначается R и определяется

R = X _max - X _min.

Информативность этого показателя невелика, хотя при малых объёмах вы­борки по размаху легко оценить разницу между лучшим и худшим результатами спортсменов.

Определение. Дисперсией называется средний квадрат отклонения значений признака от среднего арифметического.

Для несгруппированных данных дисперсия определяется по формуле

s² = 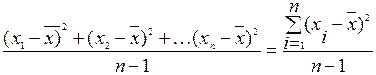, (1)

где Х_i – значение признака, 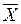- среднее арифметическое.

Для данных, сгруппированных в интервалы, дисперсия определяется по формуле

,

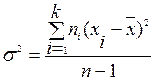где х_i – среднее значение i интервала группировки, n_i – частоты интервалов.

Для упрощения расчётов и во избежание погрешностей вычисления при округ­лении результатов (особенно при увеличении объёма выборки) используются также другие формулы для определения дисперсии. Если среднее арифметическое уже вычислено, то для несгруппированных данных используется следующая фор­мула:

s² = ,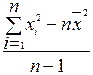

для сгруппированных данных:

.

Эти формулы получаются из предыдущих раскрытием квадрата разности под знаком суммы.

В тех случаях, когда среднее арифметическое и дисперсия вычисляются од­новременно, используются формулы:

для несгруппированных данных:

s² = ,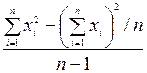

для сгруппированных данных:

.

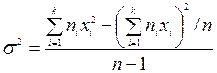3. Среднее квадратическое (стандартное) отклонение

Определение. Среднее квадратическое (стандартное) отклонение характе­ризует степень отклонения результатов от среднего значения в абсолютных единицах, т. к. в отличие от дисперсии имеет те же единицы измерения, что и результаты измерения. Иначе говоря, стандартное отклонение показывает плотность распределения результатов в группе около среднего значения, или однородность группы.

Для несгруппированных данных стандартное отклонение можно определить по формулам

s = ,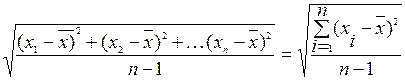

s = 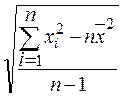или s = .

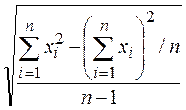Для данных, сгруппированных в интервалы, стандартное отклонение определяется по формулам:

,

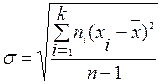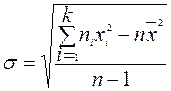или .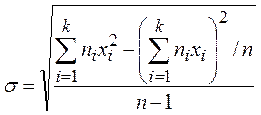

Дата добавления: 2015-07-02