Графическое представление вариационного ряда. Тема работы: Графическое представление результатов эксперимента

Пример

Тема работы: Графическое представление результатов эксперимента. Расчёт основных статистических характеристик.

Цель работы: Научиться представлять результаты исследований в графическом виде и определять основные статистические характеристики.

Условие задачи: 18 спортсменов выполняли прыжки в длину. Результаты длины прыжка Y_i (м) занесены в таблицу.

Таблица исходных данных выборки:

Таблица 3

№ п/п
Yi, м	6,35	6,83	6,25	6,38	6,42	6,35	6,51	6,06	6,22
ранжированная выборка	6,00	6,06	6,18	6,20	6,22	6,25	6,35	6,35	6,38
№ п/п
Yi, м	6,20	6,00	6,50	6,65	6,55	6,75	6,60	6,18	6,55
ранжированная выборка	6,42	6,50	6,51	6,55	6,55	6,60	6,65	6,75	6,83

Определим число интервалов по формуле Стерджеса

.

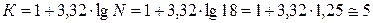Определим шаг (или ширину) интервала по формуле:

,

где - максимальное значение измеряемого показателя в упорядоченной (ранжированной) выборке; - минимальное значение показателя.

Определим шаг или ширину интервала

.

Границу интервала обычно округляют в большую сторону до размерности измеряемого показателя. Нижнюю границу первого интервала выберем равной минимальному значению выборки, то есть 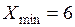. Заполним таблицу по результатам выборки (см. табл. 6), которые распределены в интервалы, т. е. результаты измерений представим в виде вариационного ряда.

В первый столбец таблицы впишем номера 5 интервалов.

Во второй столбец – границы интервала. Нижней границей первого интервала выбрали 6, прибавим к ней шаг и получим верхнюю границу первого интервала (6,00+0,17=6,17). Этот же результат является нижней границей следующего интервала (6,17+0,17=6,34) и т. д.

Значение верхней границы последнего интервала 6,85 больше максимального значения показателей выборки 6,83.

Третий столбец – срединные значения интервалов. Середину первого интервала определим как среднее арифметическое значение его границ. Середины следующих интервалов получим прибавлением шага интервала к предыдущим значениям.

Четвертый столбец – частота (n_i), т. е. количество значений, попавших в заданный интервал. Если граничный результат был учтен в интервале, то в последующем интервале учитываются значения выше граничного результата.

Пятый столбец – накопленная частота рассчитывается суммированием частот предыдущих интервалов. В последней строке столбца 4 получилось число, равное объему выборки (14).

Шестой столбец – частость (р_i^*) рассчитывается делением частоты на объём выборки.

Седьмой столбец – накопленная частость получается суммированием частостей предыдущих интервалов. В последней строке столбца 7 получилась единица.

Распределение измерений, представленное в столбцах 2(границы интервалов) и 4(частота) или 2(границы интервалов) и 6(частость), называется вариационным рядом. Напомним, что интервальным вариационным рядом называется упорядоченная совокуп­ность интервалов варьирования случайной величины с соответствующими часто­тами или частостями попаданий в каждый из них значений величины.

Представим результаты измерений в виде вариационного ряда (табл. 7).

Таблица 4

Результаты измерений, представленные в виде вариационного ряда

№ интервала	Границы интервала	Срединное значение интервала	Частота ni	Накопленная частота	Частость рi^*	Накопленная частость
	6,00 – 6,17	6,085			2/18	2/18
	6,17 – 6,34	6,255		6(2+4)	4/18	6/18
	6,34 – 6,51	6,425		12(6+6)	6/18	12/18
	6,51 – 6,68	6,595		16(12+4)	4/18	16/18
	6,68 – 6,85	6,765		18(16+2)	2/18	18/18=1

Графическое представление результатов измерений выражается в построении трех графиков: полигона частот (см. рис. 1), гистограммы (рис. 2) и полигона накопленных частот (кривой сумм или кумуляты) (рис. 4). Полигон частот и гистограмма показывают распределение измеряемых показателей и их сгруппированность вокруг среднего значения.

Для построения полигоначастот в декартовых координатах по оси абсцисс отложим срединные значения интервалов из таблицы 7, а по оси ординат – соответствующие им частоты (или частости). Для приведённого примера полигон распределения изображён на рис. 11.

Рис 11. Полигон частот результатов

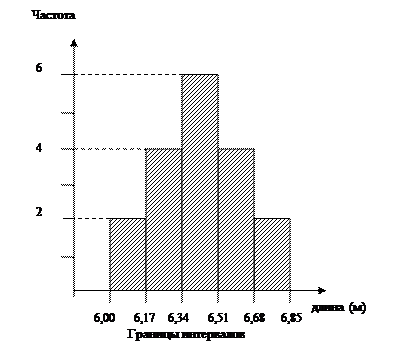
Для построения гистограммы по оси абсцисс отложим границы интервалов и на них восстановим прямоугольники до уровня частот, соответствующих интервалам, отложенных по оси ординат (рис. 12).

Рис 12. Гистограмма распределения результатов

Если нанести на гистограмму пунктирной линией полигон распределения частот, то мы получим первоначальное представление о дифференциальной функции распределения.

Как уже говорилось выше, гистограмма является экспериментальным аналогом плотности распределения вероятностей.

Площадь гистограммы равна сумме всех частот, т. е. объёму выборки (18), или сумме частостей, т. е. единице.

Рис 13. Полигон накопленных частот результатов

Для построения полигона накопленных частот (кривой сумм или кумуляты) по оси ординат отложим верхние границы интервалов, а по оси абсцисс – соответствующие им накопленные частоты (рис. 13).

Полигон накопленных частот результатов является экспериментальным аналогом функции распределения.

Далее проведём расчёт основных статистических показателей ряда измерений, он сводится к расчёту х арактеристик положения, характеристик рассеяния результатов измерений и характеристик формы распределения. Причём приведём методику расчёта с помощью формул для данных сгруппированных в интервалы.

Дата добавления: 2015-07-02