Характеристики формы распределения

Коэффициент вариации

Ошибка средней арифметической (ошибка средней)

Ошибка средней арифметической характеризует колеблемость средней и вычисляется по формуле:

.

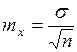Как видно из формулы, с увеличением объёма выборки ошибка средней уменьшается пропорционально корню квадратному из объёма выборки.

Коэффициент вариации определяется как отношение среднего квадратического отклонения к среднему арифметическому, выраженное в процентах:

.

Считается, что если коэффициент вариации не превышает 10 %, то выборку можно считать однородной, то есть полученной из одной генеральной совокупности.

Кривая эмпирического распределения (рис. 6) не всегда идеально колоколообразна (нормальна) и симметрична. Отсюда и следует важность вычисления коэффициентов асимметрии и эксцесса для эмпирических рядов распределения, т. к. они характеризуют скошенность и крутость данного ряда по сравнению с нормальным.

Таким образом, для многих распределений характерен сдвиг кривой влево или вправо. В связи с этим различают левостороннюю (положительную) и правостороннюю (отрицательную) асимметрию. Она зависит от знака формулы для определения коэффициента асимметрии (нормированного центрального момента третьего порядка), который служит характеристикой скошенности или асимметрии распределения, определяемой по формулам:

· для несгруппированных данных:

,

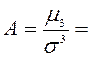
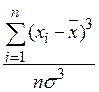где 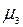- центральный момент третьего порядка, - среднее квадратическое отклонение, х_i – значение признака, 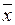- среднее арифметическое, n – объём выборки;

· для данных, сгруппированных в интервалы:

,

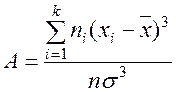где n_i – частоты интервалов группировки, x_i – срединное значение i интервала группировки, k – число интервалов.

При этом, если знак этого выражения отрицательный (-), то асимметрия правосторонняя, или отрицательная (рис. 8), если же знак положительный (+), то асимметрия левосторонняя, или положительная (рис. 9).

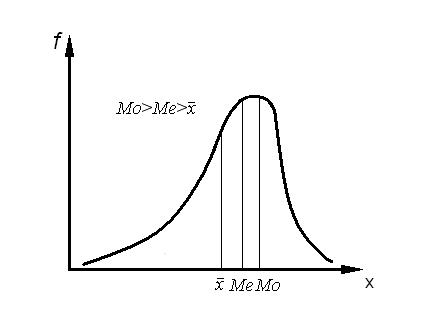
Рис. 8. Правосторонняя (отрицательная) асимметрия

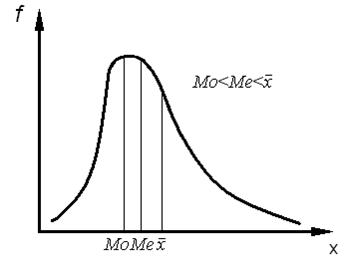
Рис. 9. Левосторонняя (положительная) асимметрия

Наиболее простой показатель асимметрии – это мера скошенности:

.

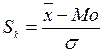В основу её положено отклонение средней арифметической от моды, а по знаку выражения определяется левосторонняя (положительная) или правосторонняя (отрицательная асимметрия).

Кроме асимметричности кривые распределения имеют характеристики плосковершинности и островершинности. Их характеристикой служит величина эксцесса (нормированного центрального момента четвёртого порядка, см. учебник), которая рассчитывается по формулам:

· для несгруппированных данных:

,

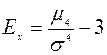
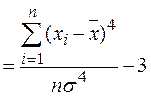где х_i - значение признака;

· для сгруппированных данных

,

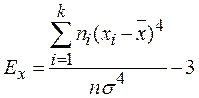где n_i - частоты интервалов группировки;

х _i - срединное значение интервала группировки;

σ - среднеквадратическое отклонение.

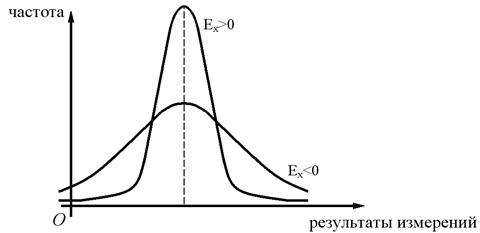
Рис. 10. Островершинная и плосковершинная кривые распределения

Если знак эксцесса отрицательный (-), то имеется тенденция к плосковершинности (рис. 10).

Если же знак положительный (+), то имеется тенденция к островершинности (рис. 10).

2. Методика выполнения расчётно-графической работы №1

Расчётно-графическая работа содержит 4 раздела.

В первом разделе:

1. Формулируется тема;

2. Формулируется цель работы.

Во втором разделе:

1. Формулируется условие задачи (в зависимости от специализации);

2. Заполняется таблица исходных данных выборки по результатам экспериментов, проведённых со спортсменами одной специализации.

В третьем разделе:

1. Результаты измерений представляются в виде вариационного ряда;

2. Даётся графическое представление вариационного ряда.

3. Формулируется вывод.

В четвёртом разделе:

1. Рассчитываются основные статистические характеристики ряда измере-ний;

2. По итогам расчётов формулируется вывод.

Оформление работы:

1. Работа выполняется в отдельной тетради или на форматных листах.

2. Титульный лист заполняется по образцу.

(Пример оформления титульного листа)

Российский Государственный Университет

физической культуры, спорта, молодёжи и туризма

Кафедра естественнонаучных дисциплин

Графическое представление результатов экспериментов

Расчёт основных статистических характеристик

Расчётно-графическая работа №1

по курсу математики

Выполнил: студент 1 к. 1 пот. 1гр.

Иванов С.М.

Преподаватель: доц. кафедры ЕНД и ИТ

(Ф.И.О.)

Москва - 2012

Пример выполнения расчётно-графической работы №1.

Дата добавления: 2015-07-02