Сравнение двух средних

В аналитической практике нередко возникает необходимость сравнения двух или большего числа средних значений. Так бывает, например, тогда, когда одну и ту же пробу анализируют разными методами. В таких случаях важно установить, является ли разница результатов статистически значимой. При рассмотрении этого вопроса сначала выясняют, насколько значима разница в дисперсиях сравниваемых значений. Проверку проводят с помощью F-критерия:

	(8.1)

F = S²₁ / S²₂,

где S²₁ – большая по значению дисперсия; S²₂ – меньшая, поэтому критерий F всегда больше единицы.

В таблицах 4 и 5 приведены числовые значения F-критерия соответственно при Р =0,95 (уровень значимости α =0,05) и Р =0,99 (уровень значимости α =0,01) и различном числе степеней свободы двух дисперсий.

Если рассчитанное по соотношению (8.1) значение F -критерия превышает табличное значение (F_табл.) при заданных вероятности и числе степеней свободы, то между дисперсиями существует значимая разница.

Если, например, в одной серии анализов из четырех определений (f=3) было получено содержание олова в бронзе с дисперсией 0,0132, а в другой серии из шести параллельных определений (f=5) дисперсия составила 0,0262, то:

F = 0,0262 / 0,0132 = 1,99

По таблицам 4 и 5 находим, что при f₁ =5, f₂ =3 и Р =0,99 значение F -критерия составляет F _{0,99; 5; 3} = 28,24, а при Р =0,95 F _{0,95; 5; 3} = 9,0. Следовательно, разница в отклонениях величин незначима даже при 5 %-ном уровне значимости, и, таким образом, обе величины следует отнести к одной и той же выборке.

Если бы F -критерий показал, что разница в дисперсиях значима, средние значения х₁ и х₂ сравнивать между собой было бы нельзя.

При незначимой разнице дисперсий находим средневзвешенную дисперсию:

(8.2)

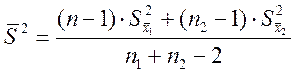
и рассчитываем критерий t:

(8.3)

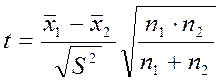
Расчет критерия t упрощается, когда один из результатов получен путем теоретического расчета, например, по стехиометрическим коэффициентам в формуле вещества. В этом случае его погрешность пренебрежимо мала и в расчет не принимается. Формула (8.3) принимает вид:

(8.4) )

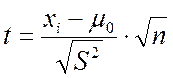
Если рассчитанное по формуле (8.3) значение t для заданного уровня значимости и числа степеней свободы f = n₁ + n₂ - 2 будет превышать величину t из таблицы 1, то различие между и является значимым.

Таблица 4

Числовые значения F_табл. при Р=0,95 (α =0,05)

Число степеней свободы, fменьш. дисп.	Число степеней свободы, fбольш. дисп.
1	2	3	4	5	6	7	8	12	24	∞
1	164,4	199,5	215,7	224,6	230,2	234,0			244,9	249,0	254,3
2	18,5	19,2	19,2	19,3	19,3	19,3			19,4	19,5	19,5
3	10,1	9,6	9,3	9,1	9,0	8,9			8,7	8,6	8,5
4	7,7	6,9	6,6	6,4	6,3	6,2			5,9	5,8	5,6
5	6,61	5,79	5,41	5,19	5,05	4,95	4,88	4,82	4,68	4,53	4,37
6	5,99	5,14	4,76	4,53	4,39	4,28	4,21	4,15	4,00	3,84	3,67
7	5,59	4,74	4,35	4,12	3,97	3,87	3,79	3,73	3,57	3,41	2,23
8	5,32	4,46	4,07	3,84	3,69	3,58	3,50	3,44	3,28	3,12	2,93
9	5,12	4,26	3,86	3,63	3,48	3,37	3,29	3,23	3,07	2,90	2,71
10	4,96	4,10	3,71	3,48	3,33	3,22	3,14	3,07	2,91	2,74	2,54
11	4,84	3,98	3,59	3,36	3,20	3,09	3,01	2,95	2,79	2,61	2,41
12	4,75	3,89	3,49	3,26	3,11	3,00	2,91	2,85	2,69	2,51	2,30
13	4,67	3,81	3,41	3,18	3,03	2,92	2,83	2,77	2,60	2,42	2,21
14	4,60	3,74	3,34	3,11	2,96	2,85	2,76	2,70	2,53	2,35	2,13
15	4,54	3,68	3,29	3,06	2,90	2,79	2,71	2,64	2,48	2,29	2,07
16	4,49	3,63	3,24	3,01	2,85	2,74	2,66	2,59	2,42	2,24	2,01
17	4,45	3,59	3,20	2,96	2,81	2,70	2,61	2,55	2,38	2,19	1,96
18	4,41	3,55	3,16	2,93	2,77	2,66	2,58	2,51	2,34	2,15	1,92
19	4,38	3,52	3,13	2,90	2,74	2,63	2,54	2,48	2,31	2,11	1,88
20	4,35	3,49	3,10	2,87	2,71	2,60	2,51	2,45	2,28	2,08	1,84
21	4,32	3,47	3,07	2,84	2,68	2,57	2,49	2,42	2,25	2,05	1,81
22	4,30	3,44	3,05	2,82	2,66	2,55	2,46	2,40	2,23	2,03	1,78
23	4,28	3,42	3,03	2,80	2,64	2,53	2,44	2,37	2,20	2,01	1,76
24	4,26	3,40	3,01	2,78	2,62	2,51	2,42	2,36	2,18	1,98	1,73
25	4,24	3,39	2,99	2,76	2,60	2,49	2,40	2,34	2,16	1,96	1,71
26	4,23	3,37	2,98	2,74	2,59	2,47	2,39	2,32	2,15	1,95	1,69
27	4,21	3,35	2,96	2,73	2,57	2,46	2,37	2,31	2,13	1,93	1,67
28	1,20	3,34	2,95	2,71	2,56	2,45	2,36	2,29	2,12	1,91	1,66
29	4,18	3,33	2,93	2,70	2,55	2,43	2,35	2,28	2,10	1,90	1,64
30	4,17	3,32	2,92	2,69	2,53	2,42	2,33	2,27	2,09	1,89	1,62
40	4,08	3,23	2,84	2,61	2,45	2,34	2,25	2,18	2,00	1,79	1,51
60	4,00	3,15	2,76	2,53	2,37	2,25	2,17	2,10	1,92	1,70	1,39
80	3,96	3,11	2,72	2,49	2,33	2,21	2,13	2,06	1,88	1,65	1,33
100	3,94	3,09	2,70	2,46	2,31	2,19	2,10	2,03	1,85	1,63	1,28
120	3,92	3,07	2,68	2,45	2,29	2,18	2,09	2,02	1,83	1,61	1,26
∞	3,84	3,00	2,61	2,37	2,22	2,10	2,01	1,94	1,75	1,52	1,00

Таблица 5

Числовые значения F_табл. при Р=0,99 (α =0,01)

Число степеней свободы, fменьш.дисп.	Число степеней свободы, fбольш.дисп.
1	2	3	4	5	6	7	8	12	24	∞
5	16,62	13,27	12,06	11,39	10,97	10,67	10,46	10,29	9,89	9,47	9,02
6	13,75	10,92	9,78	9,15	8,75	8,47	8,26	8,10	7,72	7,31	6,88
7	12,25	9,55	8,45	7,85	7,46	7,19	6,99	6,84	6,47	6,07	5,65
8	11,26	8,65	7,59	7,01	6,63	6,37	6,18	6,03	5,67	5,28	4,86
9	10,56	8,02	6,99	6,42	6,06	5,80	5,61	5,47	5,11	4,73	4,31
10	10,04	7,56	6,55	5,99	5,64	5,39	5,20	5,06	4,71	4,33	3,91
11	9,65	7,21	6,22	5,67	5,32	5,07	4,89	4,74	4,40	4,02	3,60
12	9,33	6,93	5,95	5,41	5,06	4,82	4,64	4,50	4,16	3,78	3,36
13	9,07	6,70	5,74	5,21	4,86	4,62	4,44	4,30	3,96	3,59	3,17
14	8,86	6,51	5,56	5,04	4,69	4,46	4,28	4,14	3,80	3,43	3,01
15	8,68	6,36	5,42	4,89	4,56	4,32	4,14	4,00	3,67	3,29	2,87
16	8,53	6,23	5,29	4,77	4,44	4,20	4,03	3,89	3,55	3,18	2,75
17	8,40	6,11	5,18	4,67	4,34	4,10	3,93	3,79	3,46	3,08	2,65
18	8,29	6,01	5,09	4,58	4,25	4,01	3,84	3,71	3,37	3,00	2,57
19	8,18	5,93	5,01	4,50	4,17	3,94	3,77	3,63	3,30	2,92	2,49
20	8,10	5,85	4,94	4,43	4,10	3,87	3,70	3,56	3,23	2,86	2,42
21	8,02	5,78	4,87	4,37	4,04	3,81	3,64	3,51	3,17	2,80	2,36
22	7,95	5,72	4,82	4,31	3,99	3,76	3,59	3,45	3,12	2,75	2,31
23	7,88	5,66	4,76	4,26	3,94	3,71	3,54	3,41	3,07	2,70	2,26
24	7,82	5,61	4,72	4,22	3,90	3,67	3,50	3,36	3,03	2,66	2,21
25	7,77	5,57	4,68	4,18	3,85	3,63	3,46	3,32	2,99	2,62	2,17
26	7,72	5,53	4,64	4,14	3,82	3,59	3,42	3,29	2,96	2,58	2,13
27	7,68	5,49	4,60	4,11	3,78	3,56	3,39	3,26	2,93	2,55	2,10
28	7,64	5,45	4,57	4,07	3,75	3,53	3,36	3,23	2,90	2,52	2,07
29	7,60	5,42	4,54	4,04	3,73	3,50	3,33	3,20	2,87	2,49	2,04
30	7,56	5,39	4,51	4,02	3,70	3,47	3,30	3,17	2,84	2,47	2,01
40	7,31	5,18	4,31	3,83	3,51	3,29	3,12	2,99	2,66	2,29	1,81
60	7,08	4,98	4,13	3,65	3,34	3,12	2,95	2,82	2,50	2,12	1,60
80	6,96	4,88	4,04	3,56	3,26	3,04	2,87	2,74	2,42	2,03	1,50
100	6,90	4,82	3,98	3,51	3,21	2,99	2,82	2,69	2,37	1,98	1,43
120	6,85	4,79	3,95	3,48	3,17	2,96	2,79	2,66	2,34	1,95	1,38
∞	6,64	4,61	3,78	3,32	3,02	2,80	2,64	2,51	2,19	1,79	1,00

Пример: найдем, можно ли считать значимым различие в результатах определения олова по двум методикам. Анализ четырех параллельных проб по одной методике показал массовую долю (%) олова в бронзе 4,72±0,18, а другой метод привел к результату 4,92±0,16, полученному из шести параллельных определений. Расчет по уравнению (8.1) показал, что обе дисперсии не имеют значимой разницы между собой, поэтому находим среднюю дисперсию по уравнению (8.2):

Далее по соотношению (8.3) рассчитываем коэффициент t:

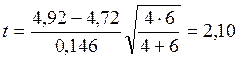
Сравнение с таблицей 1 показывает, что t _{0,95; 8} = 2,31, т.е. t_табл.> t, следовательно, значимого различия между двумя результатами не существует.

Дата добавления: 2015-07-02