Определение погрешности при многократных наблюдениях

При измерениях с многократными наблюдениями за результатом измерения принимают наиболее вероятное – среднее арифметическое выборки

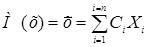
где 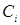- коэффициенты веса наблюдений (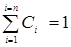). При равноточных измерениях .

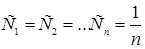Среднее арифметическое значение равно

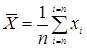
Средняя арифметическая погрешность равна 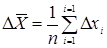, где 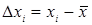- остаточные погрешности отдельных измерений.

Если результаты наблюдений можно считать принадлежащими к нормальному распределению, то оценка с.к.о. результата наблюдения G_Н определяется выражением

,

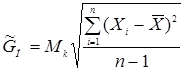где М_к – коэффициент, зависящий от числа наблюдений n.

Практически при n > 10, М_к 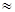1

При n < 10 значения коэффициента М_к определяются из таблицы 3.

Таблица 3.

Значения коэффициента М_к в зависимости от числа повторных измерений.

n – 1
Mк	1.253	1.128	1.085	1.064	1.051	1.042	1.036	1.032	1.028	1.025

Оценка с.к.о. результата измерения определяется следующим образом

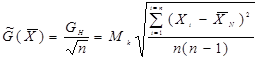
При равномерном распределении случайной погрешности оценка средне-квадратического отклонения равна

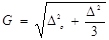, где

Δ_о – абсцисса центра интервала; Δ – абсолютное значение предельного отклонения.

Для обнаружения наблюдений, содержащих грубые погрешности используются критерий 3G и критерий Шовене. Если отклонение 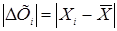>3σн, то в соответствии с первым критерием, это наблюдение содержит грубую погрешность и его следует отбросить. В соответствии с критерием Шовене отбрасываются наблюдения с отклонением ΔХ_max превышающим σн в установленное число k раз, но оно будет различным для разного числа наблюдений (табл. 5)

Таблица 5

Значение критерия Шовене

Число измерений
Коэффициент k	1.6	1.7	1.9		2.1

Дата добавления: 2015-07-02