Проверка эквивалентности двух состояний

Состояния s и t эквивалентны тогда и только тогда, когда выполняются следующие два условия:

(1) условие подобия, - состояния s и t, должны быть оба допускающими, либо оба отвергающими;

(2) условие преемственности, - для всех входных символов состояния s и t должны переходить в эквивалентные состояния, то есть их преемники должны быть эквивалентны.

Нетрудно убедиться в том, что эти два условия выполняются, когда s и t не имеют различающей цепочки.

Условия (1) и (2) можно использовать в общем методе проверки на эквивалентность двух состояний. (Изложенный ниже метод надо понимать как проверку на неэквивалентность и рассматривать как метод поиска различающей цепочки).

На рис. 3.8 (а) представлена таблица переходов конечного автомата. Проверим у него состояния 0 и 7 на эквивалентность. Оба эти состояния отвергающие, следовательно, условие подобия для них выполняется. По входному символу z состояния 0 и 7 переходят в состояние 3, эквивалентное самому себе, а по входному символу y в состояния 0 и 6 соответственно. Для состояний 0, 6 условие подобия не выполняются. Эти состояния неэквивалентны, следовательно по условию преемственности неэквивалентны и состояния 0, 7 и y - различающая их цепочка.

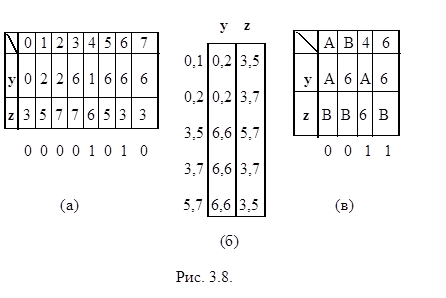
Общая процедура теста на эквивалентность основывается на построении таблицы эквивалентности и определяется следующими шагами:

1. Начать построение таблицы эквивалентности состояний с отведения столбца для каждого входного символа. Пометить первую строку парой состояний, подвергаемых проверке.

2. Выбрать в таблице эквивалентности состояний строку, ячейки которой еще не заполнены и проверить подобны ли состояния, которыми она помечена. Если они неподобны, то два исходных состояния неэквивалентны и процедура окончена. Если они подобны, вычислить результат применения каждого входного символа к этой паре состояний и записать полученные пары состояний в соответствующие ячейки рассматриваемой строки.

3. Для каждого элемента таблицы, полученного на шаге 2, существует три возможных варианта. Если элемент - пара одинаковых состояний, то для этой пары не требуется никаких действий. Если элемент - пара состояний, которые уже использовались как метка строки таблицы, то для нее также никаких действий не требуется. Наконец, если элемент - это пара разных состояний, которые еще не использовались как метка, то для нее нужно добавить строку и пометить ее этой парой. В данном случае порядок состояний s, t или t, s неважен (эквивалентность симметрична). После того, как проделаны необходимые действия с каждой парой строки, перейти к пункту 4.

4. Если все строки таблицы эквивалентности заполнены, исходная пара состояний и все пары состояний, порожденные в ходе проверки эквивалентны и проверка закончена. Если таблица не заполнена, нужно обработать по крайней мере одну строку и для нее применяется шаг 2.

На рис. 3.8 (б) приведена таблица, построенная по предложенному алгоритму и проверяющая эквивалентность состояний 0, 1 автомата с рис. 3.8 (а). Таблица полностью заполнена, следовательно 0 º 1. Но предложенный алгоритм дает значительно больше результатов. Кроме (0, 1) эквивалентны (0, 2), (3, 5), (3, 7) и (5, 7). Из 0 º 1 и 0 º 2 следует 1 º 2, то есть состояния 0, 1, 2 эквивалентны. Аналогично эквивалентны и состояния 3, 5, 7. Используя полученные результаты и сократив эквивалентные столбцы, получим новую таблицу (рис. 3.8 (в)).

Дата добавления: 2015-06-27