Линейное сжатие и ускорение автоматов

Автомат называется линейно-огранниченным по памяти, если для обработки цепочки длины n он использует не более p * n ячеек памяти.

Автомат называется линейно-ограниченным по времени, если для обработки цепочки длины n он требует не более c * n шагов по времени.

Здесь p,c ³ 1 - некоторые малые константы.

Справедлива следующая теорема о линейном сжатии.

Теорема 3.1. Если язык распознается (обрабатывается) автоматом с оценкой p * n по памяти, то можно построить автомат, распознающий тот же язык с оценкой p * n/k, где k - целое число (n ³ k ³ 1 ).

Доказательство. (Проведем его конструктивно, построением “сжатого” автомата для общего случая, когда автомат является преобразователем, то есть не только читает, но и пишет символы на ленту).

Пусть 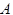- внешний алфавит, 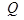- внутренний алфавит (множество состояний) исходного автомата, а k - заданная константа.

Построим новый внешний алфавит

,

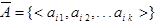состоящий из упорядоченных последовательностей по k символов старого алфавита и новое множество состояний 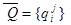, где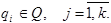

Смысл здесь состоит в том, что k старых символов из A предполагается записывать в одну клетку входной ленты.

Построим правила переходов. Пусть эти правила в исходном автомате имели вид:

,

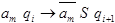что означает: “читая с ленты символ 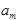и находясь в состоянии 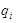, автомат записывает на ленту символ 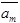, осуществляет сдвиг головки 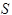, где 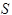может принимать значения 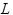(влево), 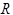(вправо) и 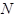(остаться на месте), и переходит в состояние 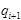“. При построении правил для нового автомата надо учитывать тот факт, что новый автомат обозревает сразу k букв старого алфавита, но на самом деле исходный автомат смотрел на 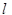-тую букву из этих k.

Правила перехода нового автомата будут иметь вид:

(а) если 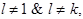то

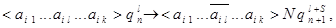
где

если в исходном автомате был сдвиг 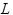входной головки;

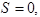если в исходном автомате был сдвиг ;

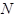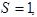если в исходном автомате был сдвиг ;

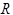(б) если 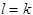и в исходном автомате был сдвиг 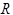, то

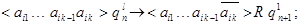
(в) если 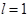и в исходном автомате был сдвиг 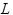, то

•

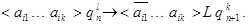С практической точки зрения такое сжатие не дает других преимуществ, кроме сокращения записи на ленте, тогда как число состояний линейно возрастает в k раз, число входных символов растет экспоненциально и время обработки цепочки не изменяется. Тем не менее, рассмотренная теорема дает основание сформулировать теорему о линейном ускорении, которую мы изложим, применительно к рассматриваемым конечным автоматам.

Теорема 3.2. Для любого конечного автомата можно построить эквивалентный ему автомат, распознающий цепочки длины n за n/k шагов, где k - целое число (n ³ k ³ 1 ).

Доказательство. Сожмем исходный автомат в k раз и заменим каждые k шагов исходного автомата одним шагом в новом ускоренном автомате. Для этого, группы правил перехода исходного автомата, имеющие вид

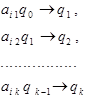
заменим на правила

. •

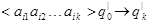Пример 3.5. Пусть автомат распознает цепочки вида dobyto, doto, doby и никаких других. Каждая правильная цепочка завершается символом #. Таким образом внешний алфавит предложенного автомата A = { d, o, b, t, # }. и его можно определить, используя восемь состояний с таблицей переходов, представленной на рис 3.11 (а).

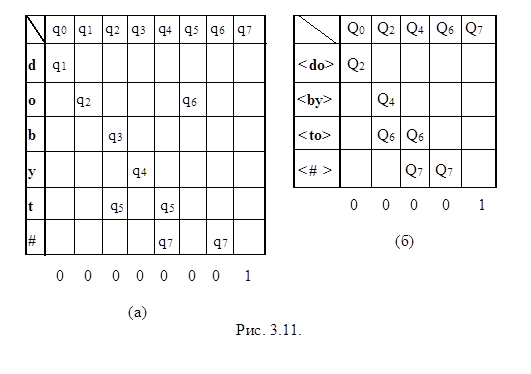
Ускорим этот автомат в два раза, а для этого сначала сожмем его вдвое и получим новый входной алфавит, содержащий пары символов

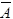= {< do >, < by >, < to >, < # >, < dy >, < db >,...}.

Хотя таких пар будет всего 25, перечислять их все не имеет смысла. Правильные сочетания - это четыре первых пары приведенного множества. Встреча со всеми остальными всегда приводит к ошибке.

Новый автомат строим, заменяя пары правил перехода исходного автомата на одно правило результирующего. Например, правила

dq₀ ® q₁

oq₁ ® q₂

заменяем на

<do> Q₀ ® Q₂,

а правила

bq₂ ® q₃

yq₃ ® q₄

на

<by> Q₂ ® Q₄.

В результате получим функциональную таблицу, приведенную на рис. 3.11 (б). Полученный автомат, обрабатывает входные цепочки за n/2 шагов. •

Выводы для практики. Реально в одну позицию - байт невозможно записать несколько символов, но используя команды ЭВМ для работы со строками или процедуры, подменяющие их, можно за одно обращение к ним пересылать или сравнивать группы символов. Если в языке требуется определенная последовательность терминальных символов в какой-то части цепочки, то соответствующую часть программы можно линейно сократить и ускорить. Так вместо группы правил

S ® wA

A ® hB

B ® iC

C ® lD

D ® eE

при обработке ключевого слова while вполне можно записать

S ® while A.

Аналогичными могут быть правила

N₁ ® if N₂

M₀ ® integer M₁

и т.п.

Дата добавления: 2015-06-27