Упражнения. 3.1. Постройте детерминированные А-грамматики для следующих цепочек, завершающихся символом “;”:

3.1. Постройте детерминированные А-грамматики для следующих цепочек, завершающихся символом “;”:

(a) целых чисел без знака и беззначащих нулей;

(б) четных целых чисел без знака;

(в) идентификаторов, содержащих четное количество символов;

(г) для цепочек из упражнения 1.5.

3.2. Постройте конечный автомат, который будет распознавать слова go to, причем между ними может быть произвольное число пробелов, включая нулевое.

3.3. Постройте конечные распознаватели для описанных ниже множеств цепочек из нулей и единиц:

(а) число единиц четное, а нулей - нечетное;

(б) между вхождениями единиц четное число нулей;

(в) за каждым вхождением пары 11 следует 0;

(г) каждый третий символ - единица;

(д) имеется по крайней мере одна единица.

3.4. Постройте конечный автомат с входным алфавитом {0,1}, который допускает в точности такое множество цепочек:

(а) все входные цепочки;

(б) все входные цепочки, кроме пустой;

(в) ни одной входной цепочки;

(г) входную цепочку 101;

(д) две входные цепочки: 01 и 0100;

(е) все входные цепочки, начинающиеся с 0 и заканчивающиеся на 1;

(ж) все цепочки, не содержащие ни одной единицы;

(з) все цепочки, содержащие в точности три единицы;

(и) все цепочки, в которых перед и после каждой единицы стоит 0;

3.5. Опишите словами множества цепочек, распознаваемых каждым из следующих автоматов:

3.6. Постройте детерминированную А-грамматику по следующей недетерминированной:

S ® aA ï aB ï bB ï bD

A ® aB ï aS ï bD

B ® cS ï cB ï bD ï b

D ® dD ï dB ï bB ï bA ï a ï c

3.7. Опишите словами множества цепочек, распознаваемых каждым из недетерминированных автоматов, изображенных на рисунке.

3.8. Найдите детерминированный автомат, эквивалентный следующему недетерминированному:

3.9. Найдите различающую цепочку (если она существует) для такой пары автоматов:

3.10. Для каждого из автоматов, приведенных ниже, найдите входную цепочку или цепочки с минимальной суммарной длиной, такие, что под их действием

(а) каждое состояние имеет место хотя бы раз;

(б) каждый переход происходит хотя бы раз.

3.11. Постройте конечный автомат, который будет допускать только те цепочки, которые можно построить из подцепочек go, goto, too, on. Возможны повторения, но не пересечения. Так, одна из допустимых цепочек goongotoongotooon. Можно сначала построить недетерминированный автомат, а затем преобразовать его в детерминированный.

3.12. Найдите недостижимые состояния автомата

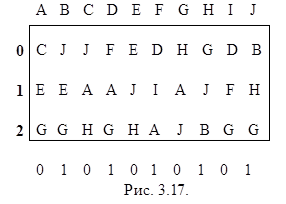
3.13. Найдите минимальные эквивалентные таблицы переходов для следующих автоматов:

Дата добавления: 2015-06-27