Показатели анализа рядов динамики

Для характеристики интенсивности изменения во времени используются следующие показатели

абсолютный прирост,

темпы роста,

темпы прироста,

абсолютное значение одного процента прироста.

Система средних показателей динамики включает следующие показатели

средний уровень ряда,

средний абсолютный прирост,

средний темп роста,

средний темп прироста.

Показатели рядов динамики можно классифицировать по следующим группам (табл. 9.1).

Таблица 9.1

Классификация показателей рядов динамики

Показатель	Базисный	Цепной	Средний
Средний уровень Конечный уровень Начальный уровень	Это сравнение с периодом (моментом) времени, начальным в ряду динамики	Это сравнение с предыдущим периодом или моментом времени	Это обобщающие итоги раз вития явления за единичный интервал или момент из имеющейся временной последовательности, определяются видом этого ряда и величиной интервала, соответствующего каждому уровню

Для интервальных рядов с равными периодами времени:

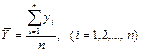, (9.1)

где 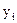- уровень ряда динамики,

n – число уровней.

Для интервальных рядов с неравными периодами времени (датами):

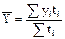, (9.2)

где 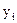- уровни ряда динамики, сохранившиеся без изменения в течение промежутка времени t_i,

t_i – количество дней между смежными датами.

Для моментных рядов с равноотстоящими моментами:

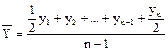(9.3)

(средняя хронологическая).

Для моментного ряда с неравными интервалами:

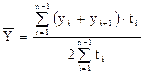, (9.4)

где y_i, y_n – уровни рядов динамики,

t_i – длительность интервала времени между уровнями.

9.4. Структура ряда динамики. Проверка ряда на наличие тренда

Всякий ряд динамики теоретически может быть представлен в виде составляющих:

тренд – основная тенденция развития динамического ряда; (к увеличению либо снижению его уровня);

циклические (периодические) колебания, в том числе сезонные;

случайные колебания.

Изучение тренда включает два основных этапа:

ряд динамики проверяется на наличие тренда;

проводится выравнивание временного ряда и непосредственное выделение тренда с экстраполяцией полученных результатов.

При составлении ряда динамики должны выполняться следующие требования:

периодизация развития, т.е. расчленение его во времени на однородные этапы, в пределах которых показатель подчиняется одному закону развития. То есть это типологическая группировка во времени. Периодизация может осуществляться несколькими методами:

а) Исторический метод осуществляется на основе узаконенной структуры динамики, при этом обращают внимание на значимые даты и события. Недостаток метода в том, что точные временные границы периодов путем теоретического анализа удается получить крайне редко.

б) Метод параллельной периодизации заключается в том, что анализируемому показателю Y, развернутому в динамический ряд {y_i}, соответствует показатель X из динамического ряда {x_i}, определяющий поведение исследуемого показателя Y. Тогда в роли однокачественных периодов развития Y нужно взять периоды X. Недостаток метода заключается в сложности нахождения X – детерминирующего показателя, зачастую которого не существует, т.к. он должен обладать весьма редкими свойствами:

связью с анализируемым показателем;

временными границами.

в) Метод многомерного статистического анализа заключается в необходимости целой системы показателей, так как учитывается многообразие аспектов явления;

амортизируется искажающее воздействие недостоверных и неточных статистических данных;

повышается обоснованность статистических выводов (экстраполяция).

статистические данные должны быть сопоставимы:

по территории;

по кругу охватываемых объектов;

по ценам;

по единицам измерения;

по времени регистрации;

по методологии расчета.

Территориальная и объемная сопоставимость обеспечивается смыканием рядов динамики, при этом либо абсолютные уровни заменяются относительными, либо делается пересчет в условные абсолютные уровни. Трудности при сопоставимости могут появиться при сравнении данных по моменту регистрации.

Величины временных интервалов должны соответствовать интенсивности изучаемых процессов. Чем больше вариация уровней во времени, тем чаще следует делать замеры. Для стабильных процессов интервалы можно увеличить.

Числовые значения уровней рядов динамики должны быть упорядоченными во времени. Не допускается анализ рядов с пропусками отдельных уровней, если же такие пропуски неизбежны, то их восполняют условными расчетными значениями.

Методы анализа основной тенденции (тренда) в рядах динамики

Одной из задач, возникающих при анализе рядов динамики, является установление закономерности изменения уровней изу­чаемого показателя во времени.

В некоторых случаях эта закономерность, общая тенденция развития объекта, вполне ясно отображается уровнями динами­ческого ряда. В одних рядах динамики наблюдается систематическое увеличение уровней ряда. Однако часто приходится встречаться с такими рядами динамики, когда уровни ряда пре­терпевают самые различные изменения (то возрастают, то убы­вают), и можно говорить лишь об общей тенденции развития яв­ления, либо о тенденции к росту, либо к снижению. В этих случа­ях для определения основной тенденции развития явления, до­статочно устойчивой на протяжении данного периода, использу­ют особые приемы обработки рядов динамики.

Уровни ряда динамики формируются под совокупным влия­нием множества длительно и кратковременно действующих фак­торов и в том числе различного рода случайных обстоятельств. Выявление основной закономерности изменения уровней ряда предполагает ее количественное выражение, в некоторой мере сво­бодное от случайных воздействий. Выявление основной тенден­ции развития (тренда) называется в статистике также вырав­ниванием временного ряда, а методы выявления основной тенден­ции - методами выравнивания. Выравнивание позволяет харак­теризовать особенность изменения во времени данного динами­ческого ряда в наиболее общем виде как функцию времени, пред­полагая, что через время можно выразить влияние всех основных факторов.

Один из наиболее простых приемов обнаружения общей тенденции развития явления - укрупнение интервала динами­ческого ряда. Смысл приема заключается в том, что первона­чальный ряд динамики преобразуется и заменяется другим, показатели которого относятся к большим по продолжитель­ности периодам времени. Например, ряд, содержащий данные о месячном выпуске продукции, может быть преобразован в ряд квартальных данных. Вновь образованный ряд может со­держать либо абсолютные величины (за укрупненные по про­должительности промежутки времени), и величины получа­ют путем простого суммирования уровней первоначального ряда абсолютных величин, либо средние величины. При сум­мировании уровней или при выведении средних по укрупнен­ным интервалам отклонения в уровнях, обусловленных слу­чайными причинами, взаимопогашаются, сглаживаются. и бо­лее четко обнаруживается действие основных факторов изме­нения уровней (общая тенденция).

Выявление основной тенденции может быть осуществлено также методом скользящей средней. Для определения скользя­щей средней формируем укрупненные интервалы, состоящие из одинакового числа уровней. Каждый последующий интервал по­лучаем, постепенно сдвигаясь от начального уровня динамиче­ского ряда на один уровень. Тогда первый интервал будет вклю­чать уровни у₁, у₂,... у_m; второй - уровни у₂,у₃,... у _m+1 и т.д. Таким образом, интервал сглаживания как бы скользит по динамическо­му ряду с шагом, равным единице. По сформированным укруп­ненным интервалам определяем сумму значений уровней, на осно­ве которых рассчитываем скользящие средние. Полученная сред­няя относится к середине укрупненного интервала. Поэтому при сглаживании скользящей средней технически удобнее укрупненный интервал составлять из нечетного числа уровней ряда. Нахождение скользящей средней по четному числу уровней создает неудобство, вызываемое тем, что средняя может быть отнесена только к середи­не между двумя датами. В этом случае необходима дополнительная процедура центрирования средних. Нередко выбор интервала сглаживания осуществляется произвольно, однако при этом нужно учитывать количество уровней в анализируемом ряду динамики, так как при использовании приема скользящей средней сглаженный ряд со­кращается по сравнению с исходным рядом на число уровней, рав­ное (m -1). Вместе с тем, чем продолжительнее интервал сглажи­вания, тем сильнее усреднение, а потому выявляемая тенденция развития получается более плавной. Чаще всего интервал сгла­живания может состоять из трех, пяти или семи уровней.

Изучение основной тенденции развития методом скользящей средней является лишь эмпирическим приемом предварительного анализа. Рассмотренные приемы сглаживания динамических ря­дов (укрупнение интервала и метод скользящей средней) могут рассматриваться как важное вспомогательное средство, облегча­ющее применение других методов и, в частности, более строгих методов выявления тенденции. Для того чтобы представить ко­личественную модель, выражающую общую тенденцию измене­ний уровней динамического ряда во времени, используется ана­литическое выравнивание ряда динамики. В этом случае фактические уровни заменяются уровнями, вычисленными на осно­ве определенной кривой. Предполагается, что она отражает об­щую тенденцию изменения во времени изучаемого показате­ля.

При аналитическом выравнивании ряда динамики закономер­но изменяющийся уровень изучаемого показателя оценивается как функция времени , где - уровни динамического ряда, вычисленные по соответствующему аналитическому урав­нению на момент времени t. Выбор формы кривой во многом определяет результаты эк­страполяции тренда. Основанием для выбора вида кривой может использоваться содержательный анализ сущности развития дан­ного явления. Можно опираться также на результаты предыду­щих исследований в данной области.

На практике для этих целей прибегают к анализу графического изображения уровней динамического ряда (линейной диаграм­мы). Однако из графического представления эмпирических дан­ных не всегда удается произвести однозначный выбор формы уравнения. Поэтому целесообразно воспользоваться графическим изображением сглаженных уровней, в которых случайные и вол­нообразные колебания в некоторой степени оказываются пога­шенными. При выборе вида кривой для выравнивания динамического ряда возможно также использование метода конечных разностей, который основан на свойствах различных кривых, применяемых при выравнивании. При выборе формы уравнения следует исходить и из объема имеющейся информации. Чем больше параметров содержит урав­нение тренда, тем больше должно быть наблюдений при одной и той же степени надежности оценивания.

Выбор формы кривой может осуществляться и на основе принятого критерия, в качестве которого может служить сум­ма квадратов отклонений фактических значений от значений, рассчитанных по уравнению тренда. Из совокупности кривых выбирается та, которой соответствует минимальное значение критерия. Рассмотрим аналитическое выравнивание ряда динамики по прямой, т.е. аналитическое уравнение вида

Y_t=b₀+b₁t, (9.5)

где t - порядковый номер периодов или моментов времени.

Параметры b₀ и b₁ прямой рассчитываются по методу наимень­ших квадратов (МНК). Система нормальных уравнений в дан­ном случае имеет вид

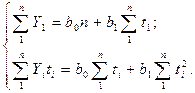(9.6)

Поиск параметров уравнения можно упростить, если отсчет времени производить так, чтобы сумма показателей времени изучаемого ряда динамики была равна нулю ( = 0). При нечетном числе уровней ряда динамики для получения 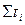= 0 уровень, находящийся в середине ряда, принимается за условное начало от­счета времени (этому периоду или моменту времени придается нулевое значение). Даты времени, стоящие выше этого уровня, обозначаются натуральными числами со знаком минус (-1,-2, -3 и т.д.), а ниже - натуральными числами со знаком плюс (+1, +2, +3 и т.д.). Если число уровней динамического ряда четное, периоды вре­мени верхней половины ряда (до середины) нумеруются -1,-3, -5 и т.д., а нижней - +1,+3,+5 и т.д. При этом условии будет равна нулю, и система нормальных уравнений преобразуется сле­дующим образом

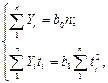откуда (9.7)

Продление в будущее тенденции, наблюдавшейся в прошлом, носит название экстраполяции. Возможность экстраполяции обеспечивается двумя обстоя­тельствами:

1) общие условия, определяющие тенденцию развития в про­шлом, не претерпевают существенных изменений в будущем;

2) тенденция развития явления характеризуется тем или иным аналитическим уравнением. Общая тенденция развития может быть охарактеризована с помощью содержательного экономического анализа. Вместе с тем расчет таких показателей, как скорость роста, темпы роста, пунк­ты роста, позволяет ориентироваться в наличии или отсутствии устойчивой тенденции развития и обосновать форму уравнения тренда. Если условия формирования уровней ряда изменяются, то расчет параметров уравнения не следует вести по данным за весь рассматриваемый период времени. В этом случае целесооб­разно разбить ряд динамики на ряд этапов, ориентируясь на устойчивость абсолютных приростов или пунктов роста. Значение у, полученное в результате экстраполяции, используют для опре­деления прогнозного значения на будущее. При составлении прогнозов оперируют не точечной, а интер­вальной оценкой, определяя так называемые доверительные ин­тервалы прогноза. Величина доверительного интервала опреде­ляется в общем виде так

Ŷ_t ± t _ά 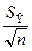, (9.8)

где S - среднее квадратическое отклонение от тренда;

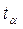- табличное значение t - критерия Стьюдента при уров­не значимости α. Величина S определяется по формуле

S = (9.9)

где у_i, и - соответственно фактические и расчетные значения уровней динамического ряда;

n - число уровней ряда;

m - количество параметров в уравнении тренда (для уравнения прямой m = 2).

Для выравнивания может использоваться парабола второго порядка

= b₀ + b₁ t + b₂ t ². (9.10)

Система нормальных уравнений для нахождения параметров уравнения параболы (при соблюдении принципа отсчета от услов­ного начала) будет иметь вид

(9.11)

Если в изменениях уровней обнаруживается тенденция к по­стоянству темпов роста, то выравнивание ряда следует проводить по показательной кривой:

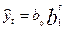, (9.12)

где 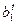- коэффициент роста.

Техника выравнивания по показательной кривой аналогична технике выравнивания по прямой, за исключением того, что вы­равниваются здесь не уровни ряда, а их логарифмы:

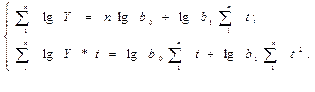(9.13)

Приравнивая 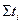⁼ 0, получаем:

(9.14)

Параметр b₀ выражает начальную скорость роста, а коэффициент b₁ – постоянную скорость изменения прироста.

По вычисленным значениям логарифмов определяем величи­ны параметров уравнения показательной кривой b₀ и b₁.

Современные компьютерные программы по анализу времен­ных рядов позволяют автоматически определять тип модели, адек­ватной исходным данным, на основе соответствующего критерия.

Аналитическое уравнение представляет собой математиче­скую модель развития явления и дает выражение статистической закономерности, проявляющейся в рядах динамики. Следует по­мнить, что прием аналитического выравнивания содержит в себе ряд условностей, связанных прежде всего с тем, что уровни, ха­рактеризующие тот или иной динамический ряд, рассматривают­ся как функция времени. В действительности же развитие явле­ний обусловлено не тем, сколько времени прошло с отправного момента, а тем, какие факторы влияли на развитие, в каком на­правлении и с какой интенсивностью. Развитие явлений во вре­мени выступает как внешнее выражение этих факторов, как их суммарное действие, оказывающее влияние на изменение уров­ня в отдельно взятые промежутки или моменты времени. Выя­вить основную тенденцию развития явления методом наимень­ших квадратов можно лишь тогда, когда выяснено, что изменяю­щиеся во времени процессы протекают на всем рассматриваемом промежутке времени одинаково, что их количественное и качест­венное изменение происходит под действием одного и того же комплекса основных факторов, определяющих движение данно­го ряда динамики.

Модели, учитывающие общие закономерности изменения эко­номического явления в изучаемый интервал времени и измене­ния во времени влияния комплекса факторов, называют много­факторными динамическими моделями.

Допустим, что величина исследуемого показателя у зависит от изменения нескольких факторов х₁, x₂, x₃..х_m. Располагая данными по некоторой совокупности объектов за ряд лет, можно по­строить корреляционную модель, характеризующую зависимость у от указанных факторов для каждого периода времени.

Предположим, что зависимость может быть представлена ли­нейной функцией. Тогда модель будет иметь вид:

для периода t = 1; ŷ₁ = a ₀₁+ a₁₁x ₁+ a ₂₁x ₂+…+ a _m1x_m;

для периода t = 2; ŷ₂ = a ₀₂+ a₁₂x ₁+ a ₂₂x ₂+…+ a _m2x_m ;

для периода t = 3; ŷ₃ = a ₀₃+ a₁₃x ₁+ a ₂₃x ₂+…+a _m31x_m и т.д.

Для всех периодов получим систему из п уравнений, и для каждого из факторов будет п коэффициентов регрессии, т.е. бу­дем иметь временные ряды для каждого из коэффициентов рег­рессии

a _01, a _02,a ₀₃ … a _0n ;

a _11, a _12,a ₁₃ … a _1n ;

a _21, a _22,a ₂₃ … a _2n ;

……………………….

a _m1, a _m2,a _m3 … a _mn.

Рассматривая каждый из этих временных рядов, можно пред­ставить а_m как функцию времени и, используя аналитическое вы­равнивание, построить прогнозы коэффициентов регрессии на пе­риод времени (t), то есть определить значение величин а_0t, а_1t, a _2t..., а _mt.

Тогда величина признака у на период t может быть представ­лена так: ŷ_t = a _0t+a_1tx ₁+a _2tx ₂+…+a _mtx_m.

Значения факторов х₁, x₂…x _m необходимо определить также на момент времени t. Обычно для этого используют либо конт­рольные цифры, либо экстраполяцию по линии тренда.

9.6. Методы выявления сезонной компоненты

Важнейшими задачами, решаемыми в ходе исследования се­зонности, являются следующие:

1) определение наличия сезонности, численное выражение проявления сезонных колебаний и выявление их силы и характе­ра в различных фазах годичного цикла;

2) характеристика факторов, вызывающих сезонные колеба­ния;

3) оценка последствий, к которым приводит наличие сезон­ных колебаний;

4) математическое моделирование сезонности.

Для измерения сезонных колебаний статистикой предложе­ны различные методы. Наиболее простые и часто употребляемые из них:

а) метод абсолютных разностей;

б) метод относительных разностей;

в) построение индексов сезонности.

Первые два способа предполагают нахождение разностей фак­тических уровней и уровней, найденных при выявлении основ­ной тенденции развития.

Применяя способ абсолютных разностей, оперируют непос­редственно размерами этих разностей, а при использовании ме­тода относительных разностей определяют отношение абсолют­ных размеров указанных разностей к выравненному уровню. При выявлении основной тенденции используют либо метод сколь­зящей средней, либо аналитическое выравнивание. В некоторых случаях в стационарных рядах можно пользоваться разностью фактических уровней и средним месячным уровнем за год.

При рассмотрении квартальных или месячных данных многих социально-экономических явлений часто обнаруживаются определенные, постоянно повторяющиеся колебания, которые существенно не изменяются за длительный период времени. Они являются результатом влияния природно-климатических условий, общих экономических факторов, а также ряда многочисленных разнообразных факторов, которые частично являются регулируемыми. В статистике периодические колебания, которые имеют определенный и постоянный период, равный годовому промежутку, носят название «сезонных колебаний» или «сезонных волн», а динамический ряд в этом случае называют тренд-сезонным, или просто сезонным рядом динамики. Сезонные колебания характеризуются специальными показателями, которые называются индексами сезонности (I_s). Совокупность этих показателей отражает сезонную волну. Индексами сезонности являются процентные отношения фактических внутригодовых уровней к постоянной или переменной средней.

Для выявления сезонных колебаний обычно берут данные за несколько лет, распределенные по месяцам. Данные за несколько лет (обычно не менее трех) берутся для того, чтобы выявить устойчивую сезонную волну, на которой не отражались бы случайные условия одного года. Если ряд динамики не содержит ярко выраженной тенденции в развитии, то индексы сезонности вычисляются непосредственно по эмпирическим данным без их предварительного выравнивания.

Для каждого месяца рассчитывается средняя величина уровня, за три года , затем из них определяется среднемесячный уровень для всего ряда 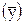и в заключении находится процентное отношение средних для каждого месяца к общему среднемесячному уровню ряда, то есть:

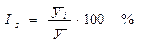. (9.15)

Если же ряд динамики содержит определенную тенденцию в развитии, то прежде чем вычислить сезонную волну, фактические данные должны быть обработаны так, чтобы была выявлена общая тенденция. Обычно для этого прибегают к аналитическому выравниванию ряда динамики.

При использовании способа аналитического выравнивания ход вычисления индексов сезонности следующий:

по соответствующему полиному вычисляются для каждого периода выровненные уровни на момент времени (t);

вычисляются отношения фактических месячных (квартальных) данных (y_i) к соответствующим выровненным данным (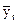) в процентах

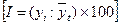; (9.16)

находятся средние арифметические из процентных соотношений, рассчитанных по одноименным периодам в процентах

(9.17)

где n – число одноименных периодов.

В общем виде формулу расчета индекса сезонности данным способом можно записать так:

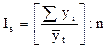. (9.18)

9.7. Элементы прогнозирования и интерполяции

Исследования динамики социально-экономических явлений, выявление и характеристика основной тенденции развития дают основание для прогнозирования – определения будущих размеров уровня экономического явления.

Важное место в системе методов прогнозирования занимают статистические методы. Применение прогнозирования предполагает, что закономерность развития, действующая в прошлом (внутри ряда динамики), сохранится и в прогнозируемом будущем, то есть прогноз основан на экстраполяции. Экстраполяция, проводимая в будущее, называется перспективой и в прошлое – ретроспективой. Обычно, говоря об экстраполяции рядов динамики, подразумевают чаще всего перспективную экстраполяцию.

В зависимости от того, какие принципы и какие исходные данные положены в основу прогноза, можно выделить следующие элементарные методы экстраполяции: среднего абсолютного прироста, среднего темпа роста и экстраполяция на основе выравнивания рядов по какой-либо аналитической формуле.

Прогнозирование по среднему абсолютному приросту может быть выполнено в том случае, если есть уверенность считать общую тенденцию линейной, то есть метод основан на предположении о равномерном изменении уровня (под равномерностью понимается стабильность абсолютных приростов).

Для нахождения интересующего нас аналитического выражения тенденции на любую дату t необходимо определить средний абсолютный прирост и последовательно прибавить его к последнему уровню ряда столько раз, на сколько периодов экстраполируется ряд, то есть экстраполяцию можно сделать по следующей формуле

, (9.19)

где - экстраполируемый уровень,

(i + t) – номер этого уровня (года);

i – номер последнего уровня (года) исследуемого периода, за который рассчитан ;

t – срок прогноза (период упреждения);

- средний абсолютный прирост.

Прогнозирование по среднему темпу роста можно осуществлять в случае, когда есть основание считать, что общая тенденция ряда характеризуется показательной (экспоненциальной) кривой. Для нахождения тенденции в этом случае необходимо определить средний коэффициент роста, возведенный в степень, соответствующую периоду экстраполяции, то есть по формуле

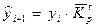, (9.20)

где y_i – последний уровень ряда динамики;

t – срок прогноза;

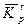- средний коэффициент роста.

Если же ряду динамики свойственна иная закономерность, то данные, полученные при экстраполяции на основе среднего темпа роста, будут отличаться от данных, полученных другими способами экстраполяции.

Рассмотренные способы экстраполяции тренда, будучи простейшими, в то же время являются и самыми приближенными. Поэтому наиболее распространенным методом прогнозирования является аналитическое выражение тренда. При этом для выхода за границы исследуемого периода достаточно продолжить значения независимой переменной времени (t).

При таком подходе к прогнозированию предполагается, что размер уровня, характеризующего явление, формируется под воздействием множества факторов, причем не представляется возможным выделить отдельно их влияние. В связи с этим ход развития связывается не с какими-либо конкретными факторами, а с течением времени, то есть y = f (t). Поэтому целесообразно определение доверительных интервалов прогноза. Величина доверительного интервала (i_g) определяется следующим образом:

i_g = 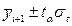, (9.21)

где 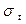- средняя квадратическая ошибка тренда;

- расчетное значение уровня;

t_α – доверительная величина.

При анализе рядов динамики иногда приходится прибегать к определению некоторых неизвестных уровней внутри данного ряда динамики, то есть к интерполяции.

Как и экстраполяция, интерполяция может производиться на основе среднего абсолютного прироста, среднего темпа роста, а также с помощью аналитического выравнивания. При интерполяции предполагается, что ни выявленная тенденция, ни ее характер не претерпели существенных изменений в том промежутке времени, уровень (уровни) которого нам неизвестен.

Контрольные вопросы

1. С какой целью анализируются данные рядов динамики?

2. Какие показатели применяются для характеристики изме­нений уровней ряда динамики?

3. Какой вид средних величин используется для расчета сред­него уровня моментного ряда динамики?

4. Охарактеризуйте роль графического представления времен­ных рядов. Назовите наиболее распространенные виды графиков.

5. Как рассчитать средний темп роста и темп прироста уров­ней ряда динамики?

6. Назовите виды колебаний уровней временного ряда.

7. Как может быть выявлена основная тенденция в изменени­ях уровней ряда динамики?

8. Назовите преимущества и роль аналитического выравни­вания уровней временного ряда.

9. Как выполнить прогноз на будущее с помощью уравнения тренда?

10. Какие факторы влияют на величину средней квадратической ошибки уравнения тренда?

11. Как рассчитать скользящую среднюю и для каких целей она может быть использована?

12. Какие методы можно использовать для выявления сезон­ных колебаний?

13. Как рассчитать индексы сезонности и осуществить экстра­поляцию с учетом сезонной составляющей?

14. Какие особенности корреляции могут быть выделены в ря­дах динамики?

Дата добавления: 2015-07-02