Краткая теория. Частным случаем физических маятников является так называемый оборотный маятник

Частным случаем физических маятников является так называемый оборотный маятник. Оборотные маятники, в зависимости от предъявляемых к ним требований, имеют самую различную форму. В настоящей работе применяется оборотный маятник, изображенный на рис. 1.

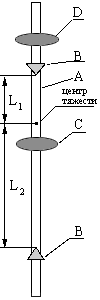На металлическом стержне А опорные призмы В жестко закреплены и не передвигаются. Жестко закреплена и чечевица С, находящаяся между ними. Вторая чечевица Д находится на конце стержня (за призмами) и может перемещаться. Ее положение фиксируется при помощи линейки, неподвижно закрепленной на стержне. Маятник ставится одной из опорных призм на неподвижно укрепленный кронштейн. При отклонении от положения равновесия маятник совершает колебательные движения. На кронштейне имеется отверстие малого диаметра, которое играет роль точки подвеса математического маятника (шарика на двойной нити (рис.2)). Нить закреплена на барабане, вращением которого можно изменять длину нити маятника, а следовательно, и его период колебаний. Двойная нить (бифилярный подвес) берется для того, чтобы колебания шарика происходили строго в одной плоскости. По периоду колебаний математического маятника Т определяется ускорение силы тяжести g в данной точке земной поверхности. При этом используется известное соотношение

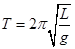, (1)

где L — длина математического маятника.

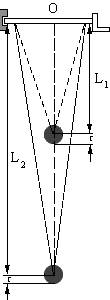Приведенной длиной маятника следует считать расстояние от точки подвеса до центра качания шарика. Центр качания можно определить как математическую точку, в которой нужно сосредоточить всю массу маятника, чтобы период его колебаний остался без изменений. Однако, непосредственное определение приведенной длины маятника может быть произведено недостаточно точно, поэтому поступают следующим образом. Измеряют длину L ¢ = L ₁ + r, где r — радиус шарика, и его длину L ¢¢ = L ₂ + r. Затем измеряют периоды свободных колебаний Т ₁ и Т ₂ маятников двух различных длин

L ¢ и L ¢¢. Из формулы (1) имеем:

.

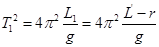
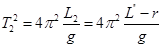Вычитая из первого выражения второе, получите формулу (2) для определения ускорения силы тяжести с помощью математического маятника. При таком способе измерения исключается необходимость измерения положения центра качания шарика.

Для определения периода колебаний используется установка, схема которой изображена на рис. 3.

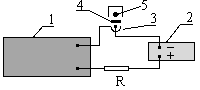Рис. 3. Блок-схема установки.

1. частотомер;

2. источник питания;

3. фотодиод;

4. флажок на маятнике;

5. источник света.

Если фотодиод закрыт флажком и не освещен, то ток в цепи слабый, т.к. темновое сопротивление фотодиода велико. При отклонении флажка фотодиод освещается, его сопротивление уменьшается и величина тока в цепи возрастает. Таким образом, во время колебаний маятника фотодиод периодически то закрывается, то освещается, соответственно, изменяется и величина электрического тока в цепи. Включенный последовательно (или параллельно) в цепь частотомер-хронометр фиксирует периодичность возникающих в цепи электрических сигналов.

Дата добавления: 2015-07-02