Работа 2

ИЗМЕРЕНИЯ

РАБОТА 1

Удостоверившись в работоспособности установки, включите приборы в сеть. Поставьте все переключатели, тумблеры и регуляторы электронного частотомер-хронометра в рабочий режим для измерения периода колебаний (необходимые данные получите у лаборанта). Установите длину маятника L ¢ и измерьте ее. Расположите осветитель и фотодиод так, чтобы в положении равновесия маятника свет на фотодиод не попадал. Отведите математический маятник на небольшой угол, отпустите шарик, предоставив ему возможность свободно колебаться.

Измерьте период колебания маятника несколько раз и запишите данные в таблицу. Форму таблицы разработайте самостоятельно.

Установите новую длину маятника L ¢¢, опустив шарик как можно ниже, и измерьте L ¢¢. Затем несколько раз измерьте период колебания маятника при этой длине и данные занесите в таблицу.

Рассчитайте ускорение свободного падения g по вашей формуле (2). Определите погрешность D g как для косвенного измерения.

Более точное определение ускорения свободного падения можно произвести с помощью оборотного маятника.

Применение оборотного маятника основано на свойстве сопряженности центра качания и точки подвеса. Это свойство заключается в том, что на всяком физическом маятнике можно найти такие две точки, что при последовательном подвешивании маятника за ту или другую из них, период колебания маятника останется одним и тем же. Расстояние между этими точками равно приведенной длине данного маятника.

Если амплитуда колебаний маятника мала, то период колебания определяется формулой

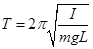, (3)

где I — момент инерции физического маятника относительно оси подвеса;

m — масса маятника;

L — расстояние между осью качания и центром тяжести маятника.

По теореме Гюйгенса-Штейнера

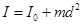, (4)

где I ₀ — момент инерции маятника относительно оси, проходящей через центр тяжести и параллельной оси качаний.

Из уравнений

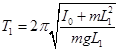, имеем

.

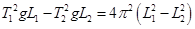Для величины ускорения из последней формулы после преобразований получаем формулу Бесселя

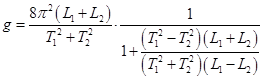. (5)

Если периоды колебаний равны между собой, то Т ₁ = Т ₂ = Т и уравнение (5) примет вид

. (6)

Но добиться полного равенства периодов нелегко. Однако формула (5) Бесселя позволяет достаточно просто и с хорошей точностью определить величину ускорения при приближенном равенстве периодов колебаний.

Перед тем, как начинать систематические измерения, необходимо подумать о том, какие следует выбрать условия опыта, чтобы точность измерений оказалась наибольшей. Чтобы ответить на этот вопрос, изучим прежде всего зависимость периода колебаний Т от расстояния L до оси качания. Рассмотрим формулу 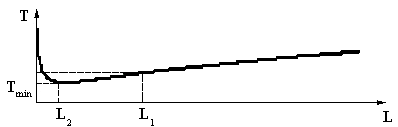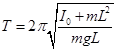. Эта зависимость имеет вид кривой, изображенной на рис. 4.

Рис. 4. График зависимости Т = f(L)

При L ® 0 период Т ® ∞, как . При L ® ∞, снова Т ® ∞, на этот раз как . При Т > Т _min одно и то же значение Т достигается при двух разных значениях L. Эти разные значения должны быть найдены на опыте и использованы для вычисления g. Как ясно из приведенного графика, при изменении Т величины L _1, L ₂ сближаются или удаляются друг от друга.

Разберем вопрос о том, как точность определения g зависит от разности L ₁ - L _2. Пусть значения Т ₁ и Т ₂ , которые нам кажутся равными, на самом деле отличаются на малую величину 2D Т, так что

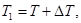
_. (7)

Величина 2D Т определяет, таким образом, точность совпадения периодов.

С помощью формул (7) вместо формулы (5) найдем (пренебрегая выражением D Т ²)

.

Введем обозначение

.

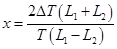Так как при достаточно малых значениях величина х будет мала, то можно воспользоваться разложением в ряд (пренебрегая членами второго и выше порядков)

,

что приводит к формуле

. (9)

В этой формуле выражение, стоящее перед скобкой, совпадает с (6), а член, вычитающийся из единицы, определяет относительную расчета g:

. (10)

Формула (10) определяет ошибку вычисления g, связанную с ошибкой измерения времени и длин. Из этого выражения видно, что относительная ошибка Dg/g неограниченно возрастает, если разность (L ₁ – L ₂ ) стремится к нулю, т.е. если Т ® Т _min (см. рис.4). Условия опыта, таким образом, должны выбираться так, чтобы L ₁ и L ₂ отличались друг от друга достаточно сильно. Измерения обычно обеспечивают хорошую точность в определении g, если .

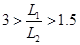Дата добавления: 2015-07-02