Введение. Рекомендовано к изданию методической комиссией механического факультета (протокол № 9 от 27 июля 2012 года ) и заседанием кафедры математики (протокол № 7 от

Уфа 2012

УДК 51(07)

ББК 22.1я73,22.161.6

М 54

Рекомендовано к изданию методической комиссией механического факультета (протокол № 9 от 27 июля 2012 года) и заседанием кафедры математики (протокол № 7 от 10 апреля 2012 года)

Составитель: доцент Лукманов Р.Л.

Рецензент: заведующий кафедрой физики Юмагужин Р.Ю.

Ответственный за выпуск: зав. кафедрой математики

доцент Лукманов Р.Л.

Одним из самых используемых методов обработки сигналов различной природы на сегодняшний день является спектральный анализ, основанный на разложении сигнала в ряд Фурье (1) по синусам и косинусам различной частоты. К примеру, полученное разложение может быть использовано в целях подавления различных «шумовых» помех. Возможны многочисленные другие приложения. В данной методической разработке приведены примеры аналитического и численного разложения в ряды Фурье различным образом заданных функций.

Разложение функции с периодом

Пусть 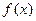- периодическая с периодом функция. Ее рядом Фурье называется ряд

, (1)

коэффициенты которого вычисляются по формулам:

(2)

(3)

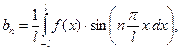(4)

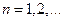
Через будем в дальнейшем обозначать сумму ряда Фурье. Оказывается, при выполнении определенных условий относительно функции 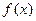ряд (1) сходится и его сумма совпадает с 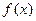. Справедлива следующая теорема.

Теорема. Если периодическая функция 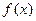с периодом кусочно-монотонна и ограничена на отрезке 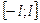, то ряд Фурье, построенный для этой функции, сходится во всех точках числовой прямой. Сумма полученного ряда равна 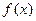в точках непрерывности функции. В точках разрыва функции 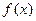сумма ряда равна среднему арифметическому пределов функции 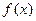слева и справа:

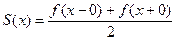. (5)

Основная работа при разложении заданной функции 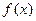в ряд Фурье заключена в вычислении интегралов в формулах (2)-(4).

Во многих случаях эти интегралы удается найти явно, аналитически. Такие примеры нами будут рассмотрены. Однако в большинстве реальных ситуаций эти интегралы приходится вычислять численно на компьютере. При этом ряд Фурье заменяется -й частичной суммой:

.

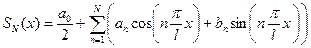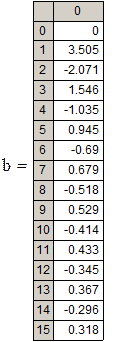
Приведем пример разложения с использованием пакета Mathcad в ряд Фурье функции

Сначала произведем периодическое продолжение этой функции на всю числовую прямую с периодом 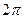. Заметим, что 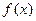имеет разрыв первого рода при , а при периодическом продолжении возникают разрывы I рода при .

 

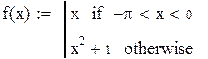
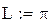
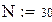
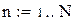
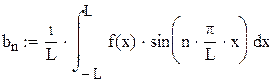
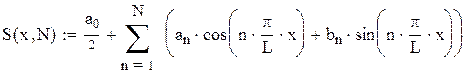
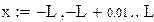
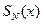Как видим, с увеличением числа отрезок ряда Фурье приближается к 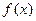в точках непрерывности функции 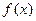. Обратим внимание на то, что точка является точкой разрыва функции 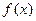, и поэтому в этой точке .

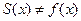Однако равенство (5) в этой точке выполнено. Это же равенство выполняется в точках разрыва , возникших при периодическом продолжении.

Обращаем Ваше внимание на то, что сходимость ряда Фурье ухудшается вблизи точек разрыва, т.е. вблизи этих точек приходится брать большее число слагаемых для достижения необходимой точности приближения.

Приведем теперь пример явного, аналитического разложения функции в ряд Фурье.

Пример. .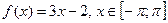

Сначала произведем периодическое продолжение заданной функции на всю числовую прямую. Исходная функция непрерывна, однако при периодическом продолжении в точках функция будет терпеть разрыв.

Вычислим коэффициенты Фурье по формулам (2)-(4).

.

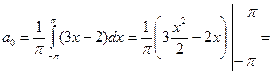
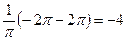
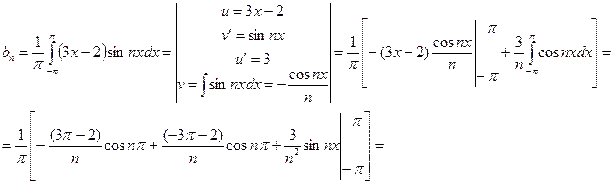
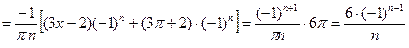Итак, получаем следующее разложение нашей функции в ряд Фурье:

.

Проиллюстрируем результат в Mathcadе:

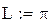
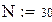
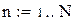
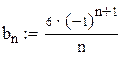
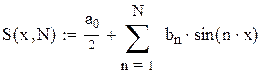
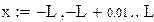
Дата добавления: 2015-07-02