
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Разложение функций с помощью четного и нечетного продолжений
|
|
|
|
Пусть 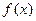 задана на отрезке
задана на отрезке  . Если эту функцию сначала продолжить четным образом на промежуток
. Если эту функцию сначала продолжить четным образом на промежуток  , а затем периодически на всю числовую прямую, то мы получим четную периодическую функцию, а значит, в ее разложении будут отсутствовать все
, а затем периодически на всю числовую прямую, то мы получим четную периодическую функцию, а значит, в ее разложении будут отсутствовать все 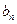 , а
, а  можно вычислять по формулам (6), (7).
можно вычислять по формулам (6), (7).
Пусть, например, нужно разложить в ряд Фурье функцию  .
.
Продолжим ее четным образом на промежуток 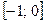 , а затем периодически на всю числовую прямую:
, а затем периодически на всю числовую прямую:

Поскольку полученная функция является четной, то коэффициенты  а
а 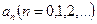 , можно вычислять по формулам (6), (7):
, можно вычислять по формулам (6), (7):
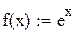
|
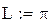
|

|
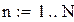
|
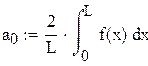
|
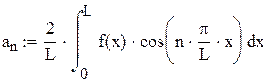
|
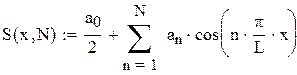

|

|
Разложим теперь эту же функцию после предварительного нечетного продолжения на промежуток 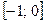 . Приведем график периодически продолженной функции:
. Приведем график периодически продолженной функции:

Воспользовавшись формулой (8) для подсчета 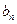 , получим:
, получим:
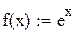
|
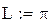
|

|
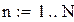
|
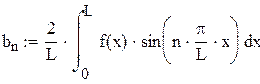
|

|

|

|
Заметим, что после нечетного продолжения  становится точкой разрыва. Кроме того, при периодическом продолжении точками разрыва будут
становится точкой разрыва. Кроме того, при периодическом продолжении точками разрыва будут 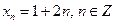 . По этой причине разложение нашей функции после нечетного продолжения будет сходиться медленнее, чем после четного из-за появления точек разрыва. Сравнивая два последних рисунка, видим, что в случае четного продолжения разложение по 5 гармоникам точнее, чем разложение по 10 гармоникам в случае нечетного продолжения.
. По этой причине разложение нашей функции после нечетного продолжения будет сходиться медленнее, чем после четного из-за появления точек разрыва. Сравнивая два последних рисунка, видим, что в случае четного продолжения разложение по 5 гармоникам точнее, чем разложение по 10 гармоникам в случае нечетного продолжения.
Отметим, что при практическом разложении сигналов в ряды Фурье, как правило, требуется найти очень большое число коэффициентов ряда, что связано с вычислением интегралов. Поскольку в явном виде они обычно не находятся, то приходится использовать численные методы, требующие больших вычислительных затрат. До относительно недавнего времени это обстоятельство сильно ограничивало возможности практического применения разложения в ряды Фурье. Прорыв в этом направлении связан с разработкой алгоритма быстрых преобразований Фурье, позволяющий многократно уменьшать вычислительные затраты. Этот алгоритм реализован в пакете Mathcad и студенты могут познакомиться с соответствующей процедурой в книге [1].
Задачи для расчетно – графического задания
Во всех задачах параметры  и
и  принять равными
принять равными  соответственно, где
соответственно, где  предпоследняя и последняя цифры номера зачетной книжки.
предпоследняя и последняя цифры номера зачетной книжки.
Разложить в ряд Фурье функцию:
1.  +
+  .
.
2. 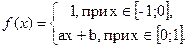
3. 
4. 
5. 
воспользовавшись
а) нечётным продолжением;
в) чётным продолжением;
6. 
7. Во всех задачах с помощью пакета Mathcad построить графики исходной функции и отрезка полученного ряда Фурье  при
при  В каких точках качество приближения функции
В каких точках качество приближения функции 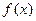 отрезком ряда Фурье хорошее, а в каких нет? Объясните почему?
отрезком ряда Фурье хорошее, а в каких нет? Объясните почему?
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Письменный Д. Т.
Конспект лекций по высшей математике: полный курс / Д. Т. Письменный. - М.: Айрис-Пресс.- 2008. – 252 с.- Ч. 2.
2. Пискунов Н. С.
Дифференциальное и интегральное исчисления: учеб. пособие для вузов / Н. С. Пискунов. - изд. стер.. - М.: Интеграл-Пресс, 2006. – 544 с.: ил. Т.2.
3. Берман Г. Н.
Сборник задач по курсу математического анализа: учеб. пособие / Г. Н. Берман. - 22-е изд., перераб. - СПб.: Профессия, 2006 - 432 с.
4. Лунгу К.Н.
Сборник задач по высшей математике: учеб. пособие / К.Н.Лунгу и др.- 7-е изд..- М.: Айрис Пресс, 2008.- 590 с.
5. Данко П. Е.
Высшая математика в упражнениях и задачах: учеб. пособие / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. - 6-е изд. - М.: ОНИКС.- 2008.- 41 с.- Ч.2.
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 1870; Нарушение авторских прав?; Мы поможем в написании вашей работы!